Với giải sách bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 4: Hình bình hành – Hình thoi

Giải SBT Toán 8 trang 65

Bài 1 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Qua O, vẽ một đường thẳng cắt AB và CD lần lượt tại M, N. Chứng minh rằng O là trung điểm của MN.

Lời giải:

Do ABCD là hình bình hành nên AB // CD, suy ra $\widehat{ODN}=\widehat{OBM}$(hai góc so le trong);

OB = OD (tính chất đường chéo của hình bình hành);

Xét ∆DON và ∆BOM ta có:

$\widehat{ODN}=\widehat{OBM}$;

OD = OB;

$\widehat{O_1}=\widehat{O_2}$ (hai góc đối đỉnh).

Suy ra ∆DON = ∆BOM (g.c.g).

Do đó OM = ON (hai cạnh tương ứng)

Vậy O là trung điểm của MN.

Bài 2 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.

a) Chứng minh rằng tứ giác AHCK là hình bình hành.

b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.

c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD

Suy ra$\widehat{ABD}=\widehat{CDB}$ (hai góc so le trong) hay $\widehat{ABH}=\widehat{CDK}$.

Xét ∆AHB vuông tại H và ∆CKD vuông tại K, ta có:

AB = CD (do ABCD là hình bình hành); $\widehat{ABH}=\widehat{CDK}$ (chứng minh trên).

Suy ra ∆AHB = ∆CKD (cạnh huyền – góc nhọn)

Do đó AH = CK (hai cạnh tương ứng)

Ta có: AH ⊥ BD, CK ⊥ BD suy ra AH // CK.

Tứ giác AHCK có: AH // CK, AH = CK nên là hình bình hành.

b) Vì AHCK là hình bình hành nên AK // CH, hay AM // CN. (1)

Hơn nữa, ABCD là hình bình hành và N ∈AD, M ∈ BC nên AN // CM. (2)

Từ (1) và (2) suy ra ANCM là hình bình hành.

Vậy AN = CM.

c) Tứ giác AHCK là hình bình hành có hai đường chéo AC, HK cắt nhau tại trung điểm

O của HK nên O cũng là trung điểm của AC.

Tứ giác ANCM là hình bình hành có hai đường chéo AC, NM cắt nhau tại trung điểm

O của AC nên O cũng là trung điểm của MN.

Vậy M, O, N thẳng hàng.

Bài 3 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Trên các cạnh AB và CD, lần lượt lấy các điểm M và N sao cho AM = CN. Gọi O là giao điểm của MN và AC. Chứng minh rằng ba điểm B, O, D thẳng hàng.

Lời giải:

Do ABCD là hình bình hành nên AB // CD, suy ra $\widehat{AMO}=\widehat{CNO};\widehat{MAO}=\widehat{NCO}$ (các cặp góc so le trong).

Xét ∆AOM và ∆CON ta có:

$\widehat{AMO}=\widehat{CNO}$ (chứng minh trên);

AM=CN (giả thiết);

$\widehat{MAO}=\widehat{NCO}$ (chứng minh trên)

Do đó ∆AOM = ∆CON (g.c.g).

Suy ra OA = OC (hai cạnh tương ứng)

Xét hình bình hành ABCD có O là trung điểm của đường chéo AC nên O cũng là trung điểm của đường chéo BD.

Do đó ba điểm B, O, D thẳng hàng.

Bài 4 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho $BM=DN=\frac{1}{3}BD$.

a) Chứng minh ∆AMB = ∆CND.

b) Chứng minh rằng tứ giác AMCN là hình bình hành.

c) Gọi O là giao điểm của AC và BD, I là giao điểm của AM và BC. Chứng minh rằng AM = 2MI.

d) Gọi K là giao điểm của CN và AD. Chứng minh I và K đối xứng với nhau qua O.

Lời giải:

a) Vì ABCD là hình bình hành nên AB = CD và AB // CD.

Suy ra $\widehat{ABM}=\widehat{CDN}$ (hai góc so le trong).

Xét ∆AMB và ∆CND, ta có:

AB = CD (chứng minh trên);

$\widehat{ABM}=\widehat{CDN}$ (chứng minh trên);

BM = DN (giả thiết).

Suy ra ∆AMB = ∆CND (c.g.c).

b) Ta có ∆AMB = ∆CND (theo câu a), suy ra AM = CN (1)

Ta có: BM + MN = BN và DN + MN = DM; mà BM = DN, suy ra BN = DM.

Xét ∆ABN và ∆CDM, ta có:

AB = CD (chứng minh trên);

$\widehat{ABN}=\widehat{CDM}$;

BN = DM (chứng minh trên)

Suy ra ∆ABN = ∆CDM (c.g.c), suy ra AN = CM (2)

Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.

c) Vì AMCN là hình bình hành nên OA = OC.

∆ABC có OA = OC, suy ra BO là đường trung tuyến của∆ABC.

ABCD là hình bình hành nên khi O là trung điểm của đường chéo AC thì O cũng là trung điểm của đường chéo BD, khi đó $BO=\frac{1}{2}BD$.

Ta lại có: $BM=\frac{1}{3}BD$, suy ra $BM=\frac{2}{3}BO$.

Do đó M là trọng tâm ∆ABC.

Khi đó $AM=\frac{2}{3}AI,MI=\frac{1}{3}AI$. Suy ra AM = 2MI.

d) Vì AMCN là hình bình hành nên AM // CN, mà M ∈ AI, N ∈ CK, nên AI // CK. (3)

Hơn nữa, AD // BC, K ∈ AD, I ∈ BC, nên AK // CI (4)

Từ (3), (4) suy ra AKCI là hình bình hành.

Mà O là trung điểm của AC, suy ra O cũng là trung điểm của KI hay I và K đối xứng nhau qua O.

Bài 5 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có AD = 2AB. Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:

a) Tứ giác MDCN là hình thoi;

b) Tam giác EMC là tam giác cân;

c) $\widehat{BAD}=2\widehat{AEM}$.

Lời giải:

a) Ta có: MF ⊥ CE, AB ⊥ CE, suy ra MN // AB // CD.

Xét tứ giác MDCN ta có: MD // CN (do AD // BC; M ∈AD, N ∈ BC) và MN // CD (chứng minh trên).

Do đó tứ giác MDCN là hình bình hành.

Mặt khác M là trung điểm của AD nên $MD=\frac{1}{2}AD$.

Lại có AD = 2AB mà AB = CD (do ABCD là hình bình hành) nên $CD=AB=\frac{1}{2}AD$.

Do đó MD = CD.

Suy ra hình bình hành MDCN là hình thoi.

b) Xét tứ giác ADCE ta có AE // CD (theo câu a).

Do đó, tứ giác ADCE là hình thang với hai đáy AE và CD.

Xét hình thang ADCE có:

M là trung điểm AD (giả thiết);

AE // MF // CD (theo câu a).

Theo chứng minh ở Bài 5, trang 63, SBT Toán 8 Tập Một, ta có: F là trung điểm của CE.

Xét ∆EMC có MF là đường trung tuyến ứng với cạnh CE và MF ⊥ CE (giả thiết).

Do đó ∆EMC cân tại M.

c) Tứ giác MDCN là hình thoi nên $\widehat{NMD}=2\widehat{NMC}$ (tính chất đường chéo của hình thoi).

Mà ∆EMC cân tại M nên $\widehat{EMF}=\widehat{CMF}$.

Ta có $\widehat{BAD}=\widehat{NMD}=2\widehat{NMC}=2\widehat{EMF}$. (1)

Lại có $\widehat{AEM}=\widehat{EMF}$ (hai góc so le trong). (2)

Từ (1) và (2) suy ra $\widehat{BAD}=2\widehat{AEM}$.

Bài 6 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD. Vẽ hình bình hành AECF (E ∈ AB, F ∈ CD). Chứng minh rằng ba đường thẳng EF, AC, BD đồng quy.

Lời giải:

Gọi O là giao điểm của AC và BD.

Vì ABCD là hình bình hành nên O là trung điểm của AC và BD.(1)

Xét hình bình hành AECF có O là trung điểm của AC nên O là trung điểm của EF (2)

Từ (1) và (2) suy ra ba đường thẳng EF, AC, BD đồng quy tại O.

Bài 7 trang 65 sách bài tập Toán 8 Tập 1: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh rằng tứ giác MNPQ là hình bình hành.

Lời giải:

Xét ∆ABD ta có M, N lần lượt là trung điểm của AB, BD (giả thiết).

Theo bài 4, trang 63, SBT Toán 8 Tập Một, ta có MN // AD và $MN=\frac{AD}{2}$.

Xét ∆ACD ta có P, Q lần lượt là trung điểm của DC, AC (giả thiết).

Theo bài 4, trang 63, SBT Toán 8 Tập Một, ta có PQ // AD và $PQ=\frac{AD}{2}$.

Xét tứ giác MNPQ ta có MN // PQ (vì cùng song song với AD) và $MN=PQ\left(=\frac{AD}{2}\right)$.

Suy ra tứ giác MNPQ là hình bình hành

Bài 8 trang 65 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OB và OD. Chứng minh tứ giác AMCN là hình bình hành.

Lời giải:

Tứ giác ABCD là hình bình hành nên OA = OC và OB = OD.

Ta có: $ON=\frac{1}{2}OD$ (N là trung điểm của OD); $OM=\frac{1}{2}OB$ (M là trung điểm của OB); OB = OD (chứng minh trên).

Suy ra OM = ON.

Xét tứ giác AMCN ta có: OM = ON, OA = OC (chứng minh trên)

Do đó, tứ giác AMCN là hình bình hành.

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Hình thang – Hình thang cân

Bài 4: Hình bình hành – Hình thoi

Bài 5: Hình chữ nhật – Hình vuông

Bài tập cuối chương 3

Bài 1: Thu thập và phân loại dữ liệu

Bài 2: Lựa chọn dạng biểu đồ để biểu diễn dữ liệu

Lý thuyết Hình bình hành – Hình thoi

I. Hình bình hành

1. Khái niệm

Hình bình hành là tứ giác có các cạnh đối song song.

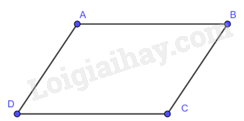
2. Hình bình hành có những tính chất gì?

Trong hình bình hành:

- Các cạnh đối bằng nhau;

- Các góc đối bằng nhau;

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết

- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

- Tứ giác có các cặp cạnh đối song song là một hình bình hành.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

- Tứ giác có các góc đối bằng nhau là một hình bình hành.

- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

II. Hình thoi

1. Khái niệm

Hình thoi là tứ giác có bốn cạnh bằng nhau.

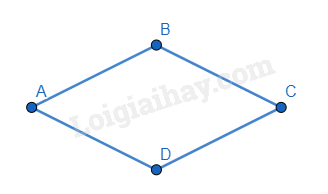
2. Tính chất

- Hai đường chéo vuông góc với nhau;

- Hai đường chéo là các đường phân giác của các góc trong hình thoi.

3. Dấu hiệu nhận biết hình thoi

- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

Ví dụ:

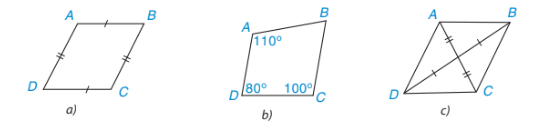
Hình a và c là hình bình hành do:

Hình a có các cặp cạnh đối bằng nhau.

Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.

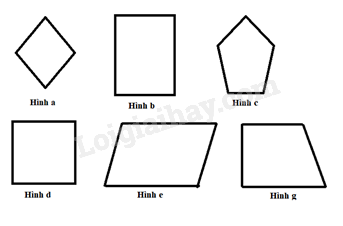
Hình a, d là hình thoi.