Với giải Bài 4 trang 66 VTH Toán lớp 8 Kết nối tri thức chi tiết trong Bài tập cuối chương 3 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải VTH Toán 8 Bài tập cuối chương 3
Bài 4 trang 66 vở thực hành Toán 8 Tập 1: Chứng minh rằng nếu nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân (H.3.43).
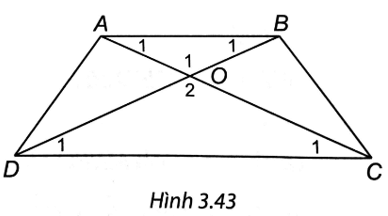
Lời giải:
Xét tứ giác ABCD đó có hai đường chéo AC = BD, hai cạnh đối AD = BC.
Hai tam giác ABD và BCA có: cạnh chung AB, AC = BD, AD = BC.
Vậy ∆ABD = ∆BCA (c.c.c).
⇒ (1)
Tương tự, ta có ∆ACD = ∆BDC (c.c.c)
⇒ (2)
Gọi O là giao của hai đường chéo AC và BD thì (hai góc đối đỉnh). (3)
Từ (1), (2), (3), ta có ⇒ AB // CD ⇒ ABCD là hình thang.
Vậy hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.
Xem thêm lời giải bài tập Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Câu 1 trang 65 vở thực hành Toán 8 Tập 1: Chọn phương án đúng.
Xem thêm các bài giải Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 15: Định lí Thalès trong tam giác
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
