Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D

Nguyễn Mạnh Tài Ngày: 22-08-2023 Lớp 8

664

Với giải Bài 3 trang 48 VTH Toán lớp 8 Kết nối tri thức chi tiết trong Bài 11: Hình thang cân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải VTH Toán 8 Bài 11: Hình thang cân

Bài 3 trang 48 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

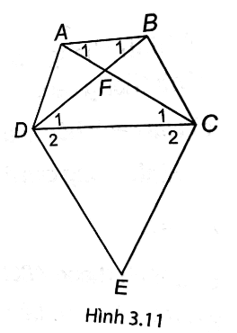
Cho hình thang ABCD (AB song song CD). Kẻ đường thẳng vuông góc với AC tại C

(H.3.11). Ta có EC = ED nên tam giác ECD cân tại E, suy ra ${\hat{D}}_{2} = {\hat{C}}_{2} .$ (1)

Do AC ⊥ CE, BD ⊥ DE nên ${\hat{D}}_{1} + {\hat{D}}_{2} = \hat{B D E} = 90 °,$ ${\hat{C}}_{1} + {\hat{C}}_{2} = \hat{A C E} = 90 ° .$ (2)

Gọi F là giao điểm của AC và BD.

Từ (1) và (2) suy ra ${\hat{D}}_{1} = {\hat{C}}_{1}$ ⇒ ∆DCF cân tại F ⇒ DF = CF (3)

Do AB // CD nên ${\hat{D}}_{1} = {\hat{B}}_{1}, {\hat{C}}_{1} = {\hat{A}}_{1}$ (hai góc so le trong).

$\Rightarrow {\hat{A}}_{1} = {\hat{B}}_{1}$ ⇒ ∆ABF cân tại F ⇒ AF = BF (4)

Từ (3) và (4) suy ra AC = AF + CF = BF + DF = BD.

Suy ra hình thang ABCD có hai đường chéo bằng nhau nên nó là hình thang cân.

Xem thêm lời giải bài tập Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Câu 1 trang 47 vở thực hành Toán 8 Tập 1: Điền cụm từ thích hợp vào chỗ trống.

Câu 2 trang 47 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD cân (AB // CD) có $\hat{C} = 60 °$ (H.3.7). Khi đó, số đo ${\hat{D}}_{1}$ bằng:

Câu 3 trang 47 vở thực hành Toán 8 Tập 1: Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).

Bài 1 trang 48 vở thực hành Toán 8 Tập 1: Hình thang trong Hình 3.9 có là hình thang cân không? Vì sao?

Bài 2 trang 48 vở thực hành Toán 8 Tập 1: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Bài 4 trang 49 vở thực hành Toán 8 Tập 1: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Bài 5 trang 49 vở thực hành Toán 8 Tập 1: Cho hình thang cân ABCD có đáy nhỏ BC. Hạ BH ⊥ AD, CE ⊥ AD.

Xem thêm các bài giải Vở thực hành Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 10: Tứ giác

Bài 11: Hình thang cân

Luyện tập chung trang 49

Bài 12: Hình bình hành

Luyện tập chung trang 54

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 9

Hai khối học sinh lớp 8 và lớp 9 của một trường trung học cơ sở tham gia lao động Lữ Ngọc My My

Toán Lớp 9

Bác Hương gửi tiết kiệm ngân hàng 100 triệu đồng với kì hạn 12 tháng Lữ Ngọc My My

Toán Lớp 9

Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v^2 + 1,1v Lữ Ngọc My My

Toán Lớp 9

Tìm hai số u và v, biết: u + v = 13 và uv = 40; u – v = 4 và uv = 77 Lữ Ngọc My My

Tìm kiếm