Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 112 bài tập chuyên đề mũ và logarit, tài liệu bao gồm 49 trang, 112 câu trắc nghiệm và có đáp án chi tiết. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
112 BÀI TẬP CHUYÊN ĐỀ MŨ – LOGARIT
LÝ THUYẾT + BÀI TẬP PHÂN CHIA THEO CẤP ĐỘ
I. LŨY THỪA
1. Lũy thừa với số mũ nguyên
- Lũy thừa với số mũ nguyên dương
\({a^n} = \mathop a\limits_{\,\,nts} a \ldots a\left( {a \in \mathbb{R},n \in {\mathbb{N}^*}} \right){\rm{. }}\)
- Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
\({a^{ - n}} = \frac{1}{{{a^n}}}\left( {n \in {Z^ + },a \in {\rm{R}}\backslash \{ 0\} } \right);{a^0} = 1.\)
- Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa với số mũ nguyên dương.
2. Căn bậc n
Cho số thực b và số nguyên dương \(n \ge 2\).
Số a được gọi là căn bậc n của b nếu \({a^n} = b\)
- Khi n lẻ, \(\forall b\) thì tồn tại duy nhất \(\sqrt[n]{b}\);
- Khi n chẵn và
+b<0 : không tồn tại căn bậc n của b;
+ b=0 : có 1 căn bậc n của b là \(\sqrt[n]{0} = 0\);
+ b>0 : có hai căn bậc n của số b là \(\sqrt[n]{b} > 0\) và \( - \sqrt[n]{b} < 0\).
3. Lũy thừa với số mũ hữu tỷ
Cho số thực a>0 và số hữu tý \(r = \frac{m}{n}\) trong đó \(m \in Z,n \in Z,n \ge 2\). Khi đó
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
4. Lũy thừa với số mũ vô tỷ
Cho \(a > 0,\alpha \in {\rm{R}}\backslash Q\) và \(\left( {{r_n}} \right)\) là 1 dãy số vô tỷ sao cho \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Khi đó
\({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\)
5. Các tính chất
- Cho hai số dương a, b và \(m,n \in {\rm{R}}\). Khi đó
\({a^m} \cdot {a^n} = {a^{m + n}}\)
\({\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m} = {a^{m \cdot n}}\)
\(\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\)
\({(a.b)^n} = {a^n}{b^n}\)
\({\left( {\frac{a}{b}} \right)^n} = \frac{{{a^n}}}{{{b^n}}}\)
- So sánh hai lũy thừa
Nếu \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
Nếu \(0 < a < 1\) thì \({a^m} > {a^n} \Leftrightarrow m < n\)
Nếu \(0 < a < b\) thì \({a^m} < {b^m} \Leftrightarrow m > 0\)
Nếu \(0 < a < b\) thì \({a^m} > {b^m} \Leftrightarrow m < 0\)
II.HÀM SỐ LŨY THỪA
1. Định nghĩa. Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) được gọi là hàm số lũy thừa
2. Tâp xác địhh.
Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) có tập xác định là
- \({\rm{R}}\) nếu \(\alpha \) nguyên dương.
- \({\rm{R}}\backslash \{ 0\} \) nếu \(\alpha \) nguyên âm hoặc \(\alpha = 0\).
- \((0; + \infty )\) nếu \(\alpha \) không nguyên.
3. Đạo hàm.
- Hàm số \(y = {x^\alpha }\) (với \(\alpha \in {\rm{R}}\) ) có đạo hàm với mọi \(x > 0\) và \({\left( {{x^\alpha }} \right)^\prime } = \alpha {x^{\alpha - 1}}\).
- Với hàm hợp \(y = {u^\alpha }\) (với \(u = u(x)\) ta có \({\left( {{u^\alpha }} \right)^\prime } = \alpha \cdot {u^{\alpha - 1}} \cdot {u^\prime }\quad (u > 0,\alpha \in {\rm{R}})\)
4. Khảo sát hàm số lũy thừa trên
|
|
|
\(\alpha < 0\) |
|
Đạo hàm |
\(y' = \alpha .{x^{\alpha - 1}}\) |
\(y' = \alpha .{x^{\alpha - 1}}\) |
|
Chiều biến thiên |
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) |
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) |
|
Tiệm cận |
Không có |
Tiệm cận ngang Ox Tiệm cận đứng Oy |
|
Đồ thị |
Đồ thị hàm số luôn đi qua điểm (1;1) |
|
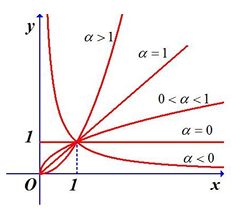
- Hình sau là đồ thị hàm số lũy thừa trên \(\left( {0; + \infty } \right)\)ứng với các giá trị khác nhau của α
III. LOGARIT
1. Định nghĩa. Cho hai số dương a, b thỏa mãn \(a > 0;a \ne 1;b > 0\). Số \(\alpha \) thỏa mãn \({a^\alpha } = b\) được gọi là logarit cơ số a của b. Kí hiệu \(\alpha = {\log _a}b\).
\({\log _a}b = \alpha \Leftrightarrow {a^a} = b\)
2. Các tính chất và quy tắc tính
Với \(a > 0;a \ne 1;b > 0;{b_1} > 0;{b_2} > 0;c > 0;c \ne 1\) ta có
- \({\log _a}1 = 0\)
- \({\log _a}a = 1\)
- \({\log _a}{a^b} = b\)
- \({a^{{{\log }_a}\alpha }} = \alpha ,(\alpha > 0)\)
- \({\log _a}\left( {{b_1} \cdot {b_2}} \right) = {\log _a}{b_1} + {\log _a}{b_2}\)
- \({\log _a}\left( {\frac{{{b_1}}}{{{b_2}}}} \right) = {\log _a}{b_1} - {\log _a}{b_2}\)
- \({\log _a}{b^a} = \alpha \cdot {\log _a}b\)
- \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\)
Đặc biệt: \({\log _a}{N^{2n}} = 2n \cdot {\log _a}|N|\)
- \({\log _c}b = {\log _c}a \cdot {\log _a}b\)
- \({\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
- \({\log _a}b = \frac{1}{{{{\log }_b}a}}(b \ne 1)\)
- \({\log _{{a^k}}}N = \frac{1}{k}{\log _a}N(k \ne 0,N > 0)\)
- \({a^{{{\log }_b}c}} = {c^{{{\log }_b}a}}\)
IV. HẢM SỐ MŨ
1. Định nghĩa. Hàm số \(y = {a^x}(a > 0,a \ne 1)\) được gọi là hàm số mũ cơ số a.
2. Giới hạn và đạo hàm của hàm số mũ
a. Giới hạn cần nhớ: \(\mathop {\lim }\limits_{t \to 0} \frac{{{e^t} - 1}}{t} = 1\)
b. Đạo hàm của hàm số mũ. Hàm số \(y = {a^x}\quad ({\rm{a}} > 0,{\rm{a}} \ne 1)\) có đạo hàm tại mọi x
- \({\left( {{e^x}} \right)^\prime } = {e^x}\)
- \({\left( {{e^u}} \right)^\prime } = {u^\prime }{e^u}\)
- \({\left( {{a^x}} \right)^\prime } = {a^x}\ln a\quad ({\rm{a}} > 0,{\rm{a}} \ne 1)\)
- \({\left( {{a^u}} \right)^\prime } = {u^\prime } \cdot {a^u}\ln a\)
|
|
0<a<1 |
a>1 |
|
|
Tập xác định |
D=R |
D=R |
|
|
Tập giá trị |
T=R+ |
T=R+ |
|
|
Chiều biến thiên |
Hàm số nghịch biến trên R |
Hàm số đồng biến trên R |
|
|
Tiệm cận |
Đồ thị nhận Ox làm tiệm cận ngang |
||
|
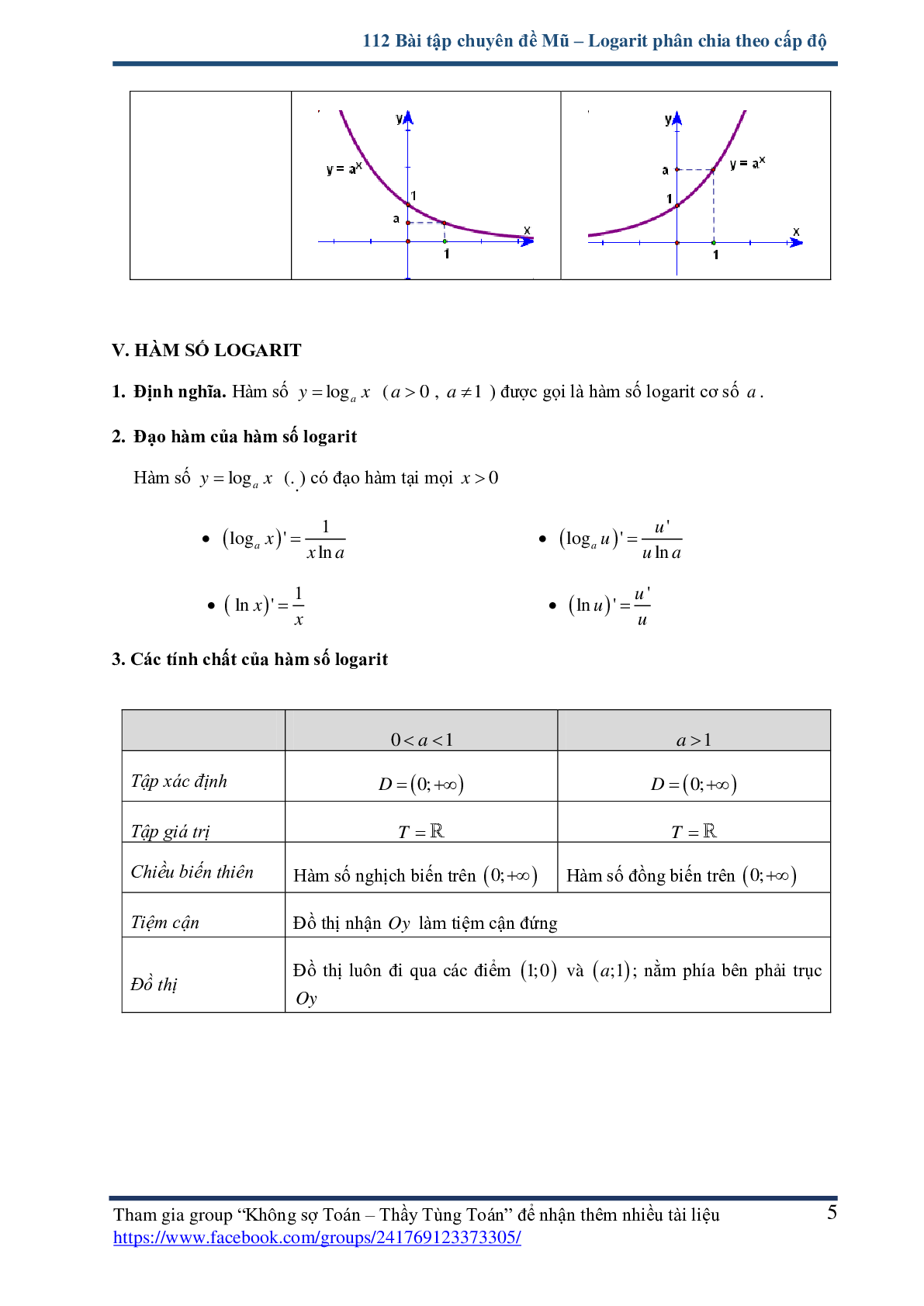
Đồ thị |
Đồ thị luôn đi qua các điểm (0;1) và (1;a) nằm phía trên trục hoành Ox |
||
|
|
|
|
|
V. HÀM SÓ LOGARIT
1. Định nghĩa. Hàm số \(y = {\log _a}x\quad (a > 0,a \ne 1)\) được gọi là hàm số logarit cơ số a.
2. Đạo hàm của hàm số logarit
Hàm số \(y = {\log _a}x\) (.) có đạo hàm tại mọi x>0
- \({\left( {{{\log }_a}x} \right)^\prime } = \frac{1}{{x\ln a}}\)
- \({\left( {{{\log }_a}u} \right)^\prime } = \frac{{{u^\prime }}}{{u\ln a}}\)
- \({(\ln x)^\prime } = \frac{1}{x}\)
\({(\ln u)^\prime } = \frac{{{u^\prime }}}{u}\)
3. Các tính chất của hàm số logarit
|
|
0<a<1 |
a>1 |
|
|
Tập xác định |
\(D = \left( {0; + \infty } \right)\) |
\(D = \left( {0; + \infty } \right)\) |
|
|
Tập giá trị |
T=R |
T=R |
|
|
Chiều biến thiên |
Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) |
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) |
|
|
Tiệm cận |
Đồ thị nhận Oy làm tiệm cận ngang |
||
|
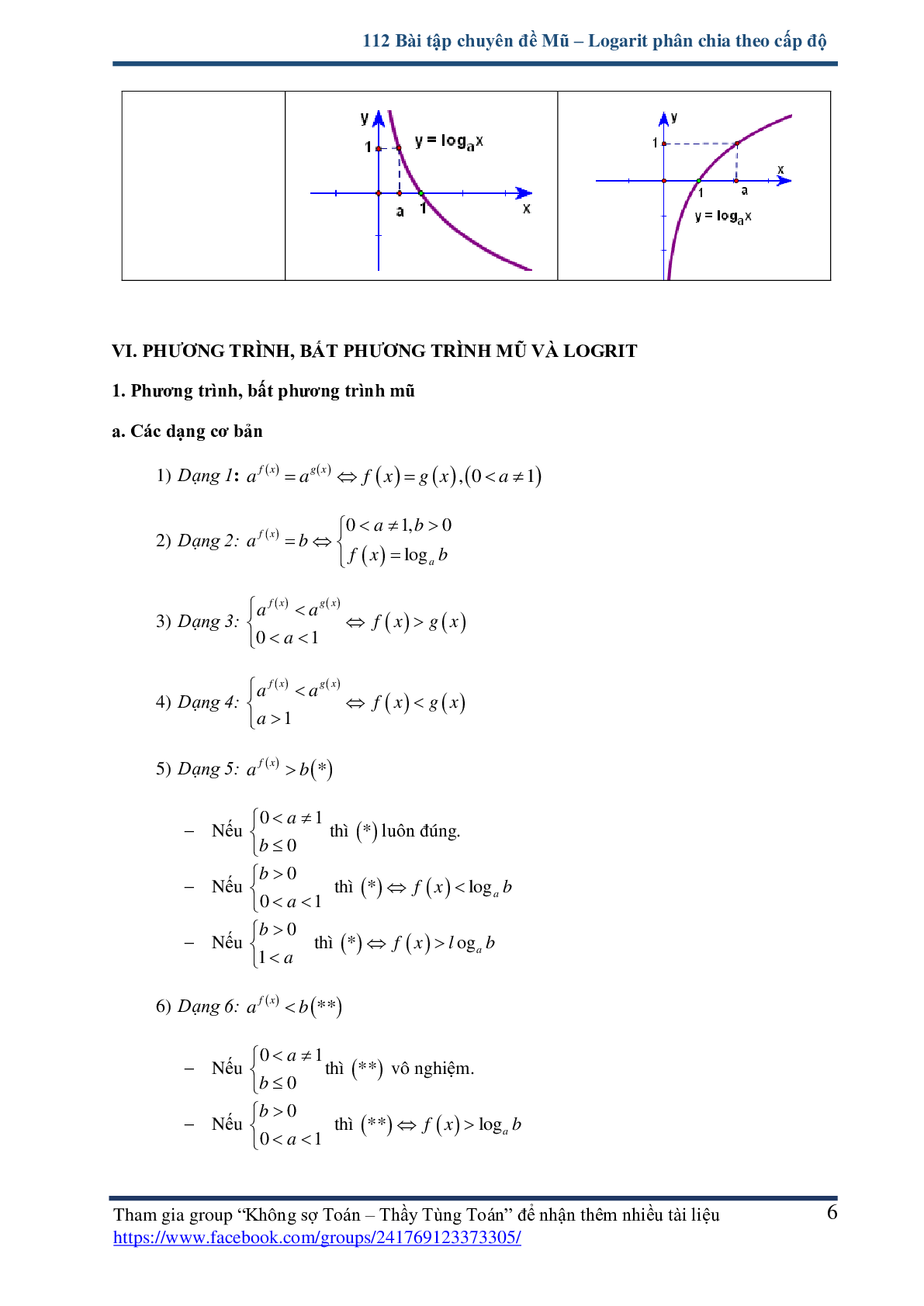
Đồ thị |
Đồ thị luôn đi qua các điểm (1;0) và (a;1) nằm phía bên phải trục Oy |
||
|
|
|
|
|