Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 1 Bài 10: Ôn tập về giải toán. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 10: Ôn tập về giải toán. Mời các bạn đón xem:
Bài tập Toán 5 Chương 1 Bài 10: Ôn tập về giải toán
A. Bài tập Ôn tập về giải toán
I. Bài tập trắc nghiệm
Câu 1. Cho các câu sau:
(1). Tìm số lớn hoặc số bé.
(2). Tìm tổng số phần bằng nhau.
(3). Tìm giá trị một phần.
Thứ tự cơ bản để giải bài toán tìm hai số khi biết tổng và tỉ số của hai số đó là:
A.
B.
C.
D.
Câu 2. Cho các câu sau:
(1) Tìm giá trị một phần.
(2) Tìm số lớn hoặc số bé.
(3) Tìm hiệu số phần bằng nhau.
Thứ tự cơ bản để giải bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó là:
A.
B.
C.
D.
Câu 3. Tổng của hai số là 135. Tỉ số của hai số là . Vậy số lớn là:
A. 81
B. 54
C. 36
D. 27
Câu 4: Hiệu của hai số là 75. Tỉ số của hai số đó là . Vậy số bé là:
A. 15
B. 165
C. 120
D. 45
Câu 5: Tổng của hai số là 270. Số thứ nhất gấp 5 lần số thứ hai. Vậy hai số đó là:
A. 45 và 225
B. 42 và 228
C. 40 và 230
D. 36 và 180
Câu 6: Lớp 5A có số học sinh nam nhiều hơn số học sinh nữ là 4 học sinh. Biết số học sinh nữ bằng số học sinh nam. Hỏi lớp 5A có bao nhiêu học sinh nam, bao nhiêu học sinh nữ?
A. 18 học sinh nữ; 22 học sinh nam
B. 22 học sinh nữ; 18 học sinh nam
C. 16 học sinh nữ; 20 học sinh nam
D. 20 học sinh nữ; 16 học sinh nam
Câu 7: Trung bình cộng của hai số là số lớn nhất có 3 chữ số khác nhau. Tìm hai số đó, biết rằng số lớn gấp đôi số bé.
A. 329 và 658
B. 650 và 1300
C. 325 và 650
D. 658 và 1316
Câu 8: Hiệu của hai số là số bé nhất có ba chữ số. Tỉ số của hai số là . Vậy tổng của hai số đó là:
A. 420
B. 350
C. 225
D. 125
II. Bài tập tự luận
Câu 1: Minh và Thắng có tất cả 56 cái bút chì. Số bút chì của Minh bằng số bút chì của Thắng. Hỏi mỗi bạn có bao nhiêu cái bút chì?
Câu 2: Một cửa hàng có số gạo nếp ít hơn số gạo tẻ là 171kg. Tính số gạo mỗi loại, biết số gạo tẻ gấp 4 lần số gạo nếp.
Câu 3: Một mảnh vườn hình chữ nhật có chu vi là 350m, chiều rộng bằng chiều dài.
a) Tính diện tích mảnh vườn hình chữ nhật đó.
b) Người ta sử dụng diện tích để trồng hoa cúc, phần đất còn lại để trồng hoa ly. Tính diện tích trồng hoa ly.
Câu 4: Nêu bài toán rồi giải bài toán theo sơ đồ sau:
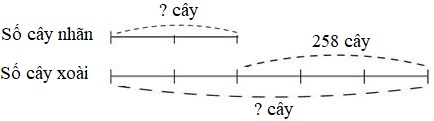
Câu 5: Bốn năm trước mẹ hơn con 32 tuổi. Ba năm nữa tuổi mẹ gấp 5 lần tuổi con. Tính tuổi của mỗi người hiện nay.
III. Bài tập vận dụng
Câu 1:
a) Tổng của hai số là 90. Số thứ nhất bằng 7/8 số thứ hai. Tìm hai số đó?
b) Hiệu của hai số là 33. Số thứ nhất bằng 8/5 số thứ hai. Tìm hai số đó?
Câu 2: Trong vườn có 64 cây cam và chanh. Số cây cam bằng 1/3 số cây chanh. Tính số cây chanh trong vườn.
Câu 3: Một sân vận động hình chữ nhật có chu vi 400m, chiều dài bằng 3/2 chiều rộng.
a) Tính chiều dài, chiều rộng của sân vận động đó?
b) Tính diện tích của sân vận động đó?
Câu 4: Một cửa hàng ngày thứ nhất bán được số đường bằng 3/5 số đường bán đươc trong ngày thứ hai. Tính số đường bán được trong mỗi ngày, biết rằng trong hai ngày đó, trung bình mỗi ngày cửa hàng bán được 40 kg đường.
Câu 5: Có tất cả 18 quả táo, cam và xoài. Số quả cam bằng 1/2 số quả táo. Số quả xoài gấp 3 lần số quả cam.
Tính số quả táo?
B. Lý thuyết Ôn tập về giải toán
* Phương pháp giải:
+ Bước 1: Vẽ sơ đồ tóm tắt đề bài
+ Bước 2: Tìm số bé và số lớn theo công thức:
Số lớn = (Tổng + Hiệu) : 2
Số bé = (Tổng – Hiệu) : 2
+ Bước 3: Kết luận (hay đáp số)
Ví dụ: Tổng hai số là 71 và hiệu hai số đó là 13. Tìm hai số đó.
Bài làm
Ta có sơ đồ:
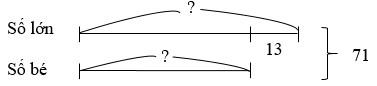
Số lớn là:
(71 + 13) : 2 = 42
Số bé là:
71 - 42 = 29
Đáp số: số bé: 29; số lớn: 42
* Định nghĩa: Tỉ số của hai số a và b là a : b hay (b khác 0)
Ví dụ: Tỉ số của hai số 3 và 5 là .
* Lưu ý: Muốn lập tỉ số của hai đơn vị đo đại lượng thì chúng phải cùng đơn vị đo.
Ví dụ: Tìm tỉ số của hai đoạn thẳng có độ dài là 1dm và 12cm.
Lời giải:
Đổi 1dm = 10cm
Tỉ số của hai đoạn thẳng trên là:
* Phương pháp giải:
+ Bước 1: Vẽ sơ đồ tóm tắt bài toán
+ Bước 2: Trình bày bài toán theo các bước:
- Tìm tổng số phần bằng nhau.
- Tìm giá trị một phần (lấy tổng ban đầu chia tổng số phần bằng nhau).
- Tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn
+ Bước 3: Kết luận (hay đáp số).
Ví dụ: Cho hai số có tổng là 63. Tìm hai số đó, biết rằng tỉ số của hai số là 4/5.
Bài làm
Ta có sơ đồ:
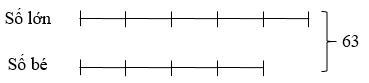
Theo sơ đồ, tổng số phần bằng nhau là:
4 + 5 = 9 (phần)
Giá trị một phần là:
63 : 9 = 7
Số bé là:
7 x 4 = 28
Số lớn là:
63 - 28 = 35
Đáp số: số bé: 28; số lớn: 35
* Phương pháp giải:
+ Bước 1: Vẽ sơ đồ tóm tắt bài toán
+ Bước 2: Trình bày bài toán theo các bước:
- Tìm hiệu số phần bằng nhau.
- Tìm giá trị một phần (lấy hiệu ban đầu chia hiệu số phần bằng nhau).
- Tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn
+ Bước 3: Kết luận (hay đáp số)
Ví dụ: Tìm hai số khi biết hiệu của hai số là 52 và tỉ số của hai số đó là 3/7.
Bài làm
Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:
7 - 3 = 4 (phần)
Giá trị một phần là:
52:4 = 13
Số lớn là:
13 x 7 = 91
Số bé là:
91 - 52 = 39
Đáp số: Số bé: 39; số lớn: 91