Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 1 Bài 8: Hỗn số. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 8: Hỗn số. Mời các bạn đón xem:

Bài tập Toán 5 Chương 1 Bài 8: Hỗn số 

A. Bài tập Hỗn số

I. Bài tập trắc nghiệm

Câu 1: Cho hình vẽ như sau:

Hỗn số thích hợp cho đối với hình vẽ đã cho là:

A. $1\frac{1}{2}$

B. $2\frac{1}{2}$

C. $2\frac{1}{3}$

D. $1\frac{1}{3}$

Câu 2:  Hỗn số $1\frac{3}{4}$ được đọc là:

A. Ba một phần tư

B. Bốn một phần ba

C. Một ba phần tư

D. Hai ba phần tư

Câu 3:  Phần nguyên của hỗn số $5\frac{4}{9}$ là:

A. 5

B.  4

C.  9

D. 3

Câu 4: Phần phân số của hỗn số $4\frac{7}{15}$ là

A. $\frac{4}{15}$

B. $\frac{15}{7}$

C. $\frac{15}{4}$

D. $\frac{7}{15}$

Câu 5:  Hỗn số $6\frac{2}{5}$ được viết dưới dạng phân số là:

A. $\frac{5}{32}$

B. $\frac{17}{5}$

C. $\frac{32}{5}$

D. $\frac{16}{5}$

Câu 6: Khi chuyển phân số $\frac{58}{9}$ thành hỗn số ta được hỗn số có phần nguyên là:

A. $6\frac{4}{9}$

B. $5\frac{13}{9}$

C. $6\frac{7}{9}$

D. $5\frac{4}{9}$

Câu 7: Điền dấu thích hợp vào chỗ chấm: $3\frac{4}{5}\cdot \cdot \cdot 3\frac{5}{6}$

A. <

B. >

C. =

D. Không so sánh được  

Câu 8: Cho các phép tính :

$$\begin{gathered} \mathrm{a})2\frac{1}{7}+3\frac{5}{7}=\frac{...}{7} \\ \mathrm{b})5\frac{2}{15}-1\frac{8}{15}=\frac{...}{15} \end{gathered}$$

Các số được điền vào các chỗ trống lần lượt là:

A. 34, 18

B. 34, 54

C. 54, 34

D. 18, 34

II. Bài tập tự luận

Câu 1: Chuyển các hỗn số sau thành phân số:

$$\begin{gathered} \mathrm{a}\left)1\frac{2}{7} \\ \mathrm{b}\right)3\frac{2}{5} \\ \mathrm{c}\left)6\frac{7}{8} \\ \mathrm{d}\right)3\frac{8}{17} \\ \mathrm{e}\left)11\frac{4}{15} \\ \mathrm{f}\right)16\frac{10}{21} \end{gathered}$$        

Câu 2: Chuyển các phân số sau thành hỗn số:

$$\begin{gathered} \mathrm{a}\left)\frac{11}{4} \\ \mathrm{b}\right)\frac{41}{6} \\ \mathrm{c}\left)\frac{77}{9} \\ \mathrm{d}\right)\frac{82}{5} \\ \mathrm{e}\left)\frac{123}{14} \\ \mathrm{f}\right)\frac{235}{24} \end{gathered}$$

Câu 3: So sánh các hỗn số sau:

a) $2\frac{9}{10}$ và $5\frac{1}{10}$

b) $7\frac{1}{2}$ và $4\frac{3}{5}$

c) $3\frac{3}{7}$ và $3\frac{2}{5}$

d) $5\frac{6}{9}$ và $5\frac{2}{3}$

Câu 4: Chuyển các hỗn số sau thành phân số rồi thực hiện các phép tính sau:

$$\begin{gathered} \mathrm{a})4\frac{1}{7}+1\frac{3}{7} \\ \mathrm{b})5\frac{3}{8}+2\frac{1}{4} \\ \mathrm{c})7\frac{1}{5}-3\frac{1}{2} \\ \mathrm{d})3\frac{2}{11}\times 2\frac{3}{7} \\ \mathrm{e})2\frac{5}{6}:3\frac{9}{11} \\ \mathrm{f})4\frac{7}{12}:3\frac{3}{4} \end{gathered}$$

Câu 5: Một cửa hàng có $72\frac{3}{4}$ kg gạo. Cửa hàng đã bán được $\frac{2}{3}$  số gạo đó, sau đó cửa hàng nhập thêm số gạo gấp 3 lần số gạo còn lại. Hỏi sau khi nhập thêm cửa hàng có tất cả bao nhiêu ki-lô-gam gạo?

Câu 6: Chuyển các phân số sau thành hỗn số rồi thực hiện phép tính:

a,	b,	c,
d,	e,	f,

Câu 7: Chuyển các phân số sau thành hỗn số (theo mẫu)

Mẫu:  Có = 2 (dư 3). Vậy 

a,

b,

c,

d,

e,

Câu 8: Chuyển hỗn số thành phân số rồi thực hiện phép tính:

a) $3\frac{1}{2}+2\frac{2}{5}=\dots$

b) $5\frac{3}{8}-1\frac{2}{3}=\dots$

c) $6\frac{3}{4}\times 3\frac{7}{13}=\dots$

d) $9\frac{5}{6}:8\frac{1}{7}=\dots$

III. Bài tập vận dụng

Câu 1: Dựa vào hình vẽ để viết rồi đọc hỗn số thích hợp:

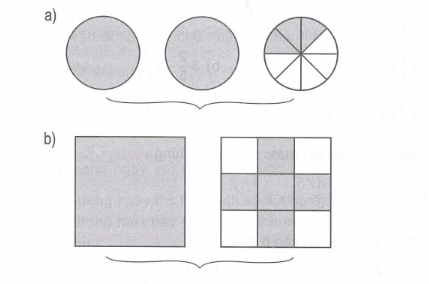
Câu 2: Khoanh vào chữ đặt trước câu trả lời đúng:

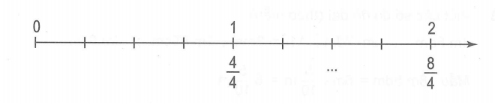
Hỗn số thích hợp để viết vào chỗ chấm dưới vạch của tia số trên là:

Câu 3: Chuyển các hỗn số sau thành phân số:

Câu 4: Đúng ghi Đ, sai ghi S:

Câu 5: Tính:

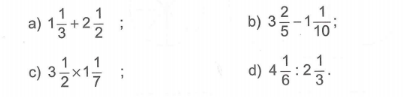
Câu 6: Một bánh xe trung bình một giây quay được  vòng. Hỏi trong  giây, bánh xe ấy quay được bao nhiêu vòng?

B. Lý thuyết Hỗn số

1. Khái niệm hỗn số

+ Khái niệm: Hỗn số gồm hai thành phần là phần nguyên và phần phân số.

Ví dụ: Cho hỗn số $3\frac{7}{12}$

Phần nguyên của hỗn số là 3 và phần phân số là $\frac{7}{12}$.

Nhận xét: Phần phân số của hỗn số bao giờ cũng bé hơn đơn vị.

+ Cách đọc hỗn số:

- Bước 1: đọc phần nguyên

- Bước 2: đọc “và”

- Bước 3: đọc phần phân số

Ví dụ: Hỗn số $3\frac{7}{12}$ được đọc là “hai và một phần tư”.

2. Cách chuyển hỗn số thành phân số

+ Để chuyển một hỗn số thành phân số, ta thực hiện các bước sau:

- Bước 1: Lấy phần nguyên nhân với mẫu số, kết quả nhận được đem cộng với tử số

- Bước 2: Thay kết quả ở bước 1 thành tử số mới, giữ nguyên mẫu số. Ta được một phân số mới được chuyển từ hỗn số đã cho

Ví dụ: Chuyển các hỗn số thành phân số: $2\frac{1}{6};5\frac{3}{4};2\frac{2}{9}$

Lời giải:

$$\begin{gathered} 2\frac{1}{6}=\frac{2\times 6+1}{6}=\frac{13}{6} \\ 5\frac{3}{4}=\frac{5\times 4+3}{4}=\frac{23}{4} \\ 2\frac{2}{9}=\frac{2\times 9+2}{9}=\frac{20}{9} \end{gathered}$$

3. Cách chuyển phân số thành hỗn số

+ Để chuyển một phân số sang hỗn số, ta thực hiện theo các bước sau:

- Bước 1: Lấy tử số chia cho mẫu số

- Bước 2: Phần nguyên là số nguyên trong hỗn số

- Bước 3: Phần dư là tử số mới trong hỗn số

- Bước 4: Phần mẫu số giữ nguyên giá trị

Ví dụ: Chuyển các phân số thành hỗn số: $\frac{9}{2};\frac{16}{3};\frac{27}{5}$

Lời giải:

Ta có:

9 : 2 = 4 (dư 1); 16 : 3 = 5 (dư 1) và 27 : 5 = 5 (dư 2)

Vậy các phân số đã cho được viết dưới dạng hỗn số là:

$$\begin{gathered} \frac{9}{2}=4\frac{1}{2} \\ \frac{16}{3}=5\frac{1}{3} \\ \frac{27}{5}=5\frac{2}{5} \end{gathered}$$

* Chú ý: Bất kỳ phân số nào có tử số lớn hơn mẫu số đều có thể đổi thành hỗn số và ngược lại. Tuy nhiên nếu tử số bằng hoặc nhỏ hơn mẫu số thì không thể thực hiện được việc chuyển phân số thành hỗn số.

4. Phép tính hỗn số

+ Tương tự như với phân số, hỗn số có thể thực hiện các phép toán cộng, trừ, nhân, chia với nhau.

+ Để cộng hay trừ hỗn số, ta có hai cách làm sau:

- Cách 1: Chuyển hỗn số về dạng phân số rồi thực hiện các phép toán trên phân số

- Cách 2: Ta tách phần nguyên để thực hiện phép tính cộng trừ, tách phần phân số rồi thực hiện phép tính cộng trừ.

Ví dụ: Thực hiện phép tính sau bằng hai cách:

a) $1\frac{5}{6}+2\frac{1}{3}$

b) $6\frac{1}{4}-1\frac{1}{12}$

Lời giải:

Cách 1:

a) $1\frac{5}{6}+2\frac{1}{3}=\frac{11}{6}+\frac{7}{3}$

$=\frac{11}{6}+\frac{14}{6}=\frac{25}{6}=4\frac{1}{6}$

b) $6\frac{1}{4}-1\frac{1}{12}=\frac{25}{4}-\frac{13}{12}$

$$\begin{gathered} =\frac{75}{12}-\frac{13}{12}=\frac{62}{12} \\ =\frac{31}{6}=5\frac{1}{6} \end{gathered}$$

Cách 2:

a) $1\frac{5}{6}+2\frac{1}{3}$

$$\begin{gathered} =\left(1+2\right)+\left(\frac{5}{6}+\frac{1}{3}\right) \\ =3+\left(\frac{5}{6}+\frac{2}{6}\right) \\ =3+\frac{7}{6}=3+1\frac{1}{6} \\ =4\frac{1}{6} \end{gathered}$$

b) $6\frac{1}{4}-1\frac{1}{12}$

$$\begin{gathered} =\left(6-1\right)+\left(\frac{1}{4}-\frac{1}{12}\right) \\ =5+\frac{1}{6}=5\frac{1}{6} \end{gathered}$$

+ Để nhân hoặc chia hỗn số, ta chuyển hỗn số về dạng phân số rồi thực hiện các phép tính nhân chia trên phân số.