Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải hay, chi tiết giúp học sinh dễ dàng làm bài tập Phương trình bậc nhất một ẩn và cách giải lớp 8.

Giải bài tập Toán lớp 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 8 Toán 8 Tập 2: Giải các phương trình:

a) x – 4 = 0;

b) $\frac{3}{4}$ + x = 0;

c) 0,5 – x = 0.

Lời giải

a) x – 4 = 0

⇔ x = 0 + 4

⇔ x = 4

Vậy phương trình có một nghiệm duy nhất x = 4.

b) $\frac{3}{4}$  + x = 0

⇔ x = 0 $-\frac{3}{4}$

⇔ x = $\frac{-3}{4}$

Vậy phương trình có một nghiệm duy nhất x= $\frac{-3}{4}$.

c) 0,5 – x = 0

⇔ x = 0,5 - 0

⇔ x = 0,5

Vậy phương trình có một nghiệm duy nhất x = 0,5.

Câu hỏi 2 trang 8 Toán 8 Tập 2: Giải các phương trình:

a) $\frac{x}{2}$  = -1;

b) 0,1x = 1,5;

c) -2,5x = 10.

Lời giải

a)  $\frac{x}{2}$= -1

⇔ x = (-1).2

⇔ x = -2

Vậy phương trình có một nghiệm duy nhất x = -2.

b) 0,1x = 1,5

⇔ x = 1,5 : 0,1

⇔ x = 15

Vậy phương trình có một nghiệm duy nhất x = 15.

c) -2,5x = 10

⇔ x = 10 : (-2,5)

⇔ x = -4

Vậy phương trình có một nghiệm duy nhất x = - 4.

Câu hỏi 3 trang 9 Toán 8 Tập 2: Giải phương trình: -0,5x + 2,4 = 0.

Lời giải

-0,5x + 2,4 = 0

⇔ -0,5x = -2,4

⇔ x = (-2,4) : (-0.5)

⇔ x = 4,8.

Vậy phương trình có một nghiệm duy nhất x = 4,8.

Bài tập (trang 9; 10)

Bài 6 trang 9 Toán 8 Tập 2: Tính diện tích S của hình thang ABCD theo x bằng hai cách:

1) Tính theo công thức: S = BH x (BC + DA) : 2

2) S = S_ABH + S_BCKH + S_CKD

Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

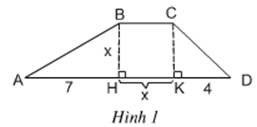
Lời giải:

1) Công thức: S = BH x (BC + DA) : 2

+ Có BH ⊥ HK, CK ⊥ HK (giả thiết)

Mà BC // HK (vì ABCD là hình thang)

Do đó: BH ⊥ BC, CK ⊥ BC

Tứ giác BCKH có bốn góc vuông nên BCKH là hình chữ nhật.

Mặt khác: BH = HK = x (giả thiết) nên BCKH là hình vuông.

⇒ BH = BC = CK = KH = x

+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.

Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2

= x.(2x + 11) : 2 = $\frac{2x^2+11x}{2}$.

2) S = S_ABH + S_BCKH + S_CKD

+ ABH là tam giác vuông tại H

⇒ S_BAH = $\frac{1}{2}$ .BH.AH = $\frac{1}{2}$.7.x = $\frac{7x}{2}$.

+ BCKH là hình chữ nhật

⇒ S_BCKH = x.x = x².

+ CKD là tam giác vuông tại K

⇒ S_CKD = $\frac{1}{2}$.CK.KD = $\frac{1}{2}$.4.x = 2x.

Do đó: S = S_ABH + S_BCKH + S_CKD 

= $\frac{7x}{2}$ + x² + 2x = x² + $\frac{11x}{2}$.

- Với S = 20 ta có phương trình:

Theo cách tính 1 ta có:   $\frac{2x^2+11x}{2}$ = 20.

Theo cách tín 2 ta có: x² + $\frac{11x}{2}$  = 20

Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.

Bài 7 trang 10 Toán 8 Tập 2: Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:

a) 1 + x = 0;

b) x + x² = 0;

c) 1 – 2t = 0;

d) 3y = 0.

e) 0x – 3 = 0.

Lời giải:

Phương trình dạng ax+ b= 0, với a, b là hai số đã cho và a ≠ 0 , được gọi là phương trình bậc nhất một ẩn.

+ Phương trình 1 + x = 0 x + 1 = 0 là phương trình bậc nhất với a = 1 ; b = 1.

+ Phương trình x + x² = 0 không phải phương trình bậc nhất vì có chứa x² .

+ Phương trình 1 – 2t = 0 -2t + 1 = 0 là phương trình bậc nhất ẩn t với a = -2 và b = 1.

+ Phương trình 3y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0.

+ Phương trình 0x – 3 = 0 không phải phương trình bậc nhất vì hệ số bậc nhất a = 0.

Bài 8 trang 10 Toán 8 Tập 2: Giải các phương trình:

a) 4x – 20 = 0;

b) 2x + x + 12 = 0;

c) x – 5 = 3 – x;

d) 7 – 3x = 9 – x.

Lời giải:

a) 4x – 20 = 0

⇔ 4x = 20

⇔ x = 20 : 4

⇔ x = 5

Vậy phương trình có nghiệm duy nhất x = 5.

b) 2x + x + 12 = 0

⇔ 3x + 12 = 0

⇔ 3x = -12

⇔ x = -12 : 3

⇔ x = -4

Vậy phương trình đã cho có nghiệm duy nhất x = -4.

c) x – 5 = 3 – x

⇔ x + x = 5 + 3

⇔ 2x = 8

⇔ x = 8 : 2

⇔ x = 4

Vậy phương trình có nghiệm duy nhất x = 4.

d) 7 – 3x = 9 – x

⇔ -3x + x= 9 - 7

⇔ -2x = 2

⇔ x = 2 : (-2)

⇔ x = -1

Vậy phương trình có nghiệm duy nhất x = -1.

Bài 9 trang 10 Toán 8 Tập 2: Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.

a) 3x – 11 = 0;

b) 12 + 7x = 0;

c) 10 – 4x = 2x – 3.

Lời giải:

a) 3x – 11 = 0

⇔ 3x = 11

⇔$x=11:3$ .

$\iff x=\frac{11}{3}\approx 3,67$

Vậy nghiệm của phương trình là $x\approx 3,67$.

b) 12 + 7x = 0

⇔7x = -12

$\iff x=-12:7$

⇔ $x=\frac{-12}{7}\approx -1,71$.

Vậy nghiệm của phương trình là $x\approx -1,71$.

c) 10 – 4x = 2x – 3.

⇔ -4x – 2x = -3 – 10

⇔ -6x = -13

$\iff x=(-13):(-6)$

⇔ $x=\frac{13}{6}\approx 2,17$

Vậy nghiệm của phương trình là $x\approx 2,17$.