Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 7 Bài 4: Định lí và chứng minh một định lí sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 4: Định lí và chứng minh một định lí. Mời các bạn đón xem:
Trắc nghiệm Toán 7 Bài 4: Định lí và chứng minh một định lí
I. Nhận biết
Câu 1. Cho phát biểu: “Chứng minh định lí là dùng … để từ … suy ra …”.
Các cụm từ thích hợp điền vào chỗ trống lần lượt là:
A. Hình vẽ, giả thiết, kết luận;
B. Giả thiết, hình vẽ, kết luận;
C. Giả thiết, lập luận, kết luận;
D. Lập luận, giả thiết, kết luận.
Đáp án: D
Giải thích:
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Do đó các cụm từ cần điền vào chỗ trống lần lượt là: lập luận, giả thiết, kết luận.
Câu 2. Trong các câu sau, câu nào không phải định lí
A. Nếu hai góc bằng nhau thì chúng đối đỉnh;
B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;
C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;
D. Nếu hai góc đối đỉnh thì chúng bằng nhau.
Đáp án: A
Giải thích:
Hai góc bù nhau là hai góc có tổng số đo bằng 180° nên C đúng.
Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau mà hai góc bù nhau là hai góc có tổng số đo bằng 180° nên B đúng.
Hai góc đối đỉnh thì bằng nhau nên D đúng.
Hai góc bằng nhau chưa chắc đã đối đỉnh nên khẳng định này sai.
Chẳng hạn:
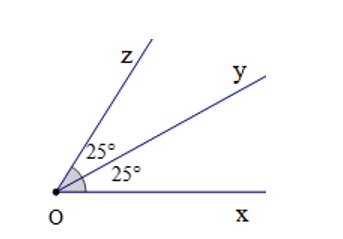
Ví dụ: (cùng bằng 25°) nhưng là hai góc kề nhau, không phải là hai góc đối đỉnh.
Do đó phương án A không phải là một định lí nên A sai.
Câu 3. “Định lí” bao gồm các thành phần:
A. Giả thiết và định nghĩa;
B. Định nghĩa và kết luận;
C. Định nghĩa;
D. Giả thiết và kết luận.
Hướng dẫn giải
Đáp án: D
Giải thích:
Vì giả thiết của định lí là điều cho biết và kết luận của định lí là điều được suy ra.
Do đó một định lí bao gồm 2 thành phần là: giả thiết và kết luận.
Câu 4. Cho các phát biểu sau:
Khi định lí được phát biểu dưới dạng “ Nếu… thì…”
(I) Phần nằm giữa chữ “Nếu” và chữ “thì” là phần giả thiết.
(II) Phần nằm giữa chữ “Nếu” và chữ “thì” là phần lập luận.
(III) Phần nằm sau chữ “thì” là phần kết luận.
Chọn khẳng định đúng:
A. (I) và (II) đúng;
B. (II) và (III) đúng;
C. (I) và (III) đúng;
D. Cả 3 đều đúng.
Đáp án: C
Giải thích:
Một định lí bao gồm phần giả thiết và kết luận. Giả thiết của định lí là điều cho biết và kết luận của định lí là điều được suy ra.
Do đó khi định lí được phát biểu dưới dạng “ Nếu… thì…”, phần nằm giữa chữ “Nếu” và chữ “thì” là phần giả thiết, phần nằm sau chữ “thì” là phần kết luận.
Nên (I) và (III) đúng còn (II) sai.
Câu 5. Phát biểu nào sau đây là đúng?
A. Định lí là một suy luận được suy ra từ những lập luận được cho là đúng;
B. Định lí là một khẳng định được suy ra từ những khẳng định được cho là đúng;
C. Định lí là một lập luận được suy ra từ những khẳng định được cho là đúng;
D. Định lí là một giả thiết được suy ra từ những khẳng định được cho là đúng.
Đáp án: B
Giải thích:
Định lí là một khẳng định được suy ra từ những khẳng định được cho là đúng, nên B đúng
II. Thông hiểu
Câu 1. Cho giả thiết: “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba”. Kết luận nào dưới đây là đúng để được một định lí hoàn chỉnh:
A. “thì chúng cắt nhau”;
B. “thì chúng vuông góc với nhau”;
C. “thì chúng song song với nhau”;
D. “thì chúng trùng nhau”.
Đáp án: C
Giải thích:
Định lí: Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Câu 2. Một định lí được minh họa bởi hình vẽ:
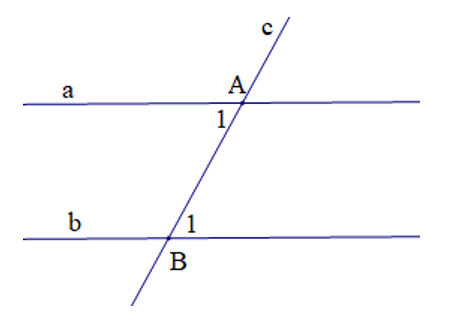
Định lí có giả thiết và kết luận như sau:

Định lí được phát biểu thành lời là:
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc bất kì bằng nhau;
B. Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau nhau thì hai đường thẳng đó song song;
C. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau;
D. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có tổng bằng 180°.
Đáp án: C
Giải thích:
Từ giả thiết và kết luận ta có: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong và bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Câu 3. Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau”. Kết luận của định lí là
A. Hai góc so le trong bằng nhau;
B. Hai góc đồng vị bằng nhau;
C. Hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau;
D. Cả 3 đều sai.
Đáp án: C
Giải thích:
Khi định lí được phát biểu dưới dạng “ Nếu… thì…”, phần nằm giữa chữ “Nếu” và chữ “thì” là phần giả thiết, phần nằm sau chữ “thì” là phần kết luận.
“ Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau” là một định lí có:
+ Giả thiết: một đường thẳng cắt hai đường thẳng song song;
+ Kết luận: hai góc so le trong bằng nhau, hai góc đồng vị bằng nhau.
Do đó C đúng, A và B sai.
Câu 4. Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. Giả thiết của định lí là
A. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba;
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba;
C. Chúng song song với nhau;
D. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.
Đáp án: B
Giải thích:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là một định lí có:
+ Giả thiết: hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba;
+ Kết luận: chúng song song với nhau.
Do đó A, C, D sai ; B đúng
Câu 5. Cho các khẳng định sau:
(1) Nếu hai đường thẳng song song thì không có điểm chung.
(2) Nếu hai đường thẳng cắt nhau thì vuông góc.
(3) Nếu hai đường thẳng có điểm chung thì cắt nhau.
(4) Nếu OA = OB thì O là trung điểm của AB.
Có bao nhiêu khẳng định là định lí?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: B
Giải thích:
(1) Nếu hai đường thẳng song song thì không có điểm chung, đây là khẳng định đúng.
Do đó đây là một định lí.

(2) Nếu hai đường thẳng cắt nhau thì vuông góc, đây là khẳng định sai nên không phải là một định lí.
Vì hai đường thẳng cắt nhau nếu không tạo thành góc vuông thì hai đường thẳng đó không vuông góc với nhau.
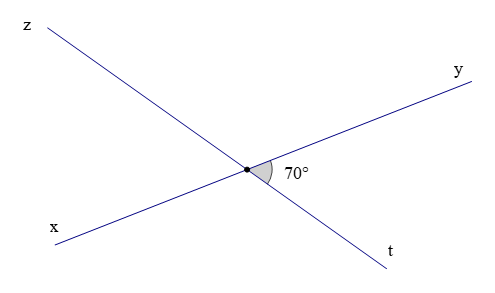
(3) Nếu hai đường thẳng có điểm chung thì cắt nhau, đây là khẳng định sai nên không phải là một định lí.
Vì hai đường thẳng trùng nhau có vô số điểm chung.
(4) Nếu OA = OB thì O là trung điểm của AB, đây là khẳng định sai nên không phải là một định lí.
Vì nếu OA = OB mà 3 điểm O, A, B không thẳng hàng thì O không thể là trung điểm của AB.
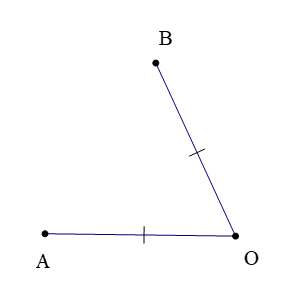
Do đó chỉ có khẳng định (1) đúng nên có 1 định lí đúng.
Câu 6. Cho định lí: “Hai tia phân giác của hai góc kề bù thì tạo thành một góc vuông” được minh họa bởi hình vẽ dưới đây:
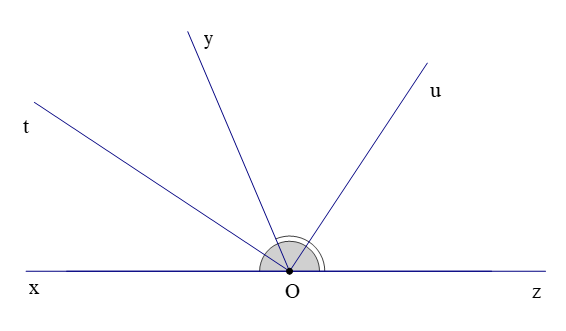
Kết luận của định lí là:
A. ;
B. ;
C. ;
D. .
Đáp án: C
Giải thích:
“Hai tia phân giác của hai góc kề bù thì góc tạo thành một góc vuông” là định lí có:
+ Giả thiết: và là hai góc kề bù, Ot là tia phân giác của , Ou là tia phân giác của ;
+ Kết luận:
Câu 7. Phần giả thiết: c cắt a tại điểm E, c cắt b tại điểm F và (như hình vẽ) là của định lí nào sau đây?
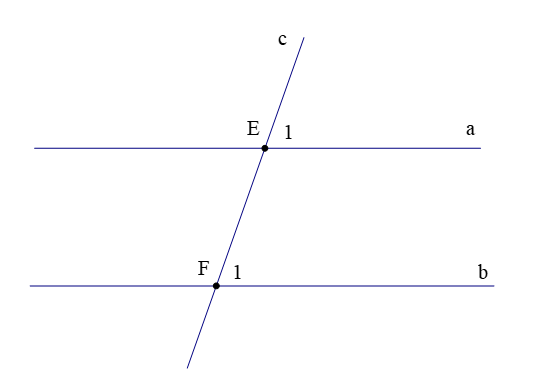
A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau;
B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song với nhau;
C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc kề bù bằng nhau thì hai đường thẳng đó song song với nhau;
D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đối đỉnh bằng nhau thì hai đường thẳng đó song song với nhau.
Đáp án: B
Giải thích:
Theo bài ta có: c cắt a tại điểm E, c cắt b tại điểm F và
Mà và là hai góc ở vị trí đồng vị.
Nên định lí đúng là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song với nhau”.
Do đó B đúng.
III. Vận dụng
Câu 1. Cho giả thiết “Hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau, được minh họa như hình vẽ dưới đây:
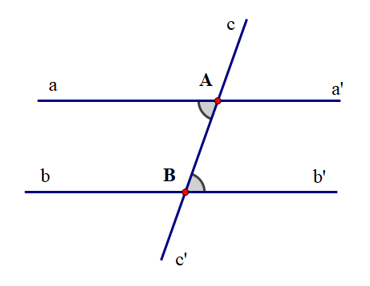
Kết luận nào sau đây là sai:
A.
B.
C. =
D.
Đáp án: D
Giải thích:
+ Ta có (giả thiết)
Mà (hai góc đối đỉnh)
Suy ra (vì cùng bằng ).
Do đó A là kết luận đúng.
+ Ta có (giả thiết)
Mà (hai góc đối đỉnh)
Suy ra (vì cùng bằng ).
Do đó B là kết luận đúng.
+ Ta có + = 180° (hai góc kề bù)
Và + = 180° (hai góc kề bù)
Mà
Suy ra = .
Do đó C là kết luận đúng.
+ Ta có = (hai góc đối đỉnh)
= (hai góc đối đỉnh)
Mà =
Suy ra .
Do đó D là kết luận sai.
Câu 2. Cho hình vẽ minh họa cho giả thiết: aa' cắt cc’ tại A; bb' cắt cc’ tại B; aa’ // bb’.
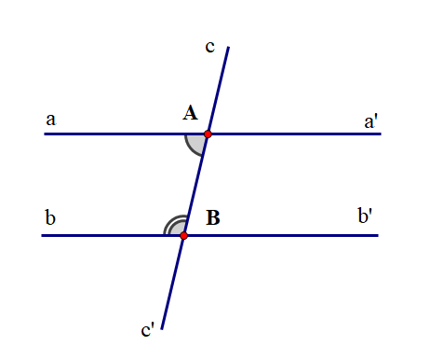
Cho các kết luận sau:
(I)
(II)
(III)
Có bao nhiêu kết luận là đúng?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: D
Giải thích:
+ Vì và là hai góc kề bù nên
Suy ra
Do đó (I) đúng.
+ Ta có aa’ // bb’ (giả thiết) nên (hai góc so le trong).
Do đó (II) đúng.
+ Ta có aa’ // bb’ (giả thiết) nên (hai góc so le trong)
Mà (chứng minh trên)
Suy ra
Do đó (III) đúng.
Vậy có 3 kết luận đúng.
Câu 3. Để chứng minh định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”, ta có thể sử dụng khẳng định nào sau đây:
A. “Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau”;
B. “Nếu hai đường thẳng phân biệt cùng cắt đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”;
C. “Hai góc có tổng bằng 180° thì bù với nhau”;
D. “Nếu hai đường thẳng cắt nhau và trong các góc tạo thành có một góc bằng 90° thì vuông góc với nhau”.
Đáp án: B
Giải thích:
Định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra từ: “Nếu hai đường thẳng phân biệt cùng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì chúng song song với nhau”.
Thật vậy ta có thể chứng minh định lí như sau:
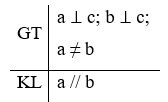
Chứng minh (hình vẽ dưới đây):
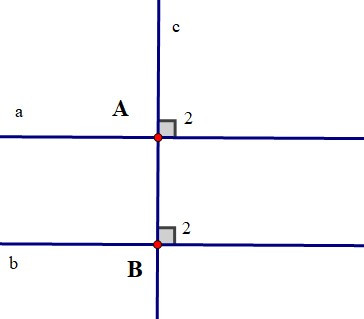
Ta có a ⊥ c (giả thiết) suy ra ;
b ⊥ c (giả thiết) suy ra
Do đó
Mà và là hai góc ở vị trí đồng vị.
Suy ra a // b.
Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 3. Hai đường thẳng song song
Trắc nghiệm Bài 4. Định lí và chứng minh một định lí