Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 7 Chương 4: Góc và đường thẳng song song sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 7.
Trắc nghiệm Toán 7 Chương 4: Góc và đường thẳng song song
I. Nhận biết
Câu 1. Cho a // b, đường thẳng c cắt hai đường thẳng a, b lần lượt tại E và F sao cho .
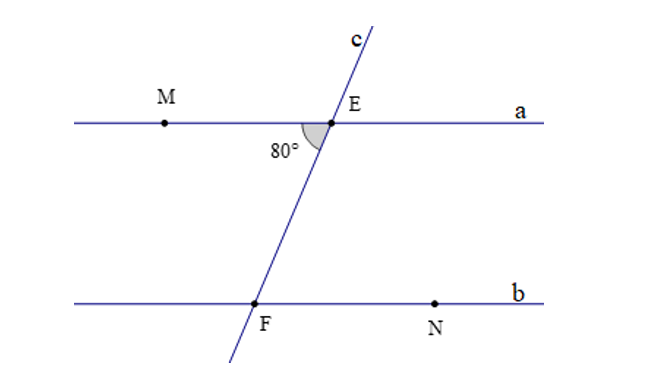
Số đo là
A. 40°;
B. 80°;
C. 100°;
D. 140°.
Đáp án: B
Giải thích:
Theo bài ta có a // b mà và là hai góc ở vị trí so le trong.
Do đó (tính chất của hai đường thẳng song song)
Mà nên
Câu 2. Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. Giả thiết của định lí là
A. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba;
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba;
C. Chúng song song với nhau;
D. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.
Đáp án: B
Giải thích:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là một định lí có:
+ Giả thiết: hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba;
+ Kết luận: chúng song song với nhau.
Do đó A, C, D sai ; B đúng
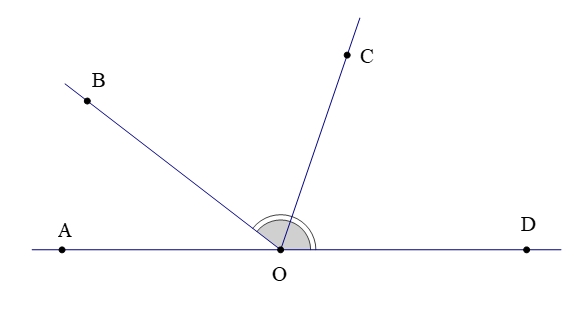
Câu 3. Quan sát hình vẽ.
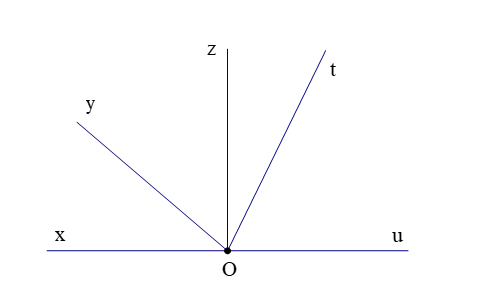
Có tất cả bao nhiêu góc kề (không kể góc bẹt) với ?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
Do đó các góc kề với là:
Vậy có tất cả 3 góc kề (không kể góc bẹt) với .
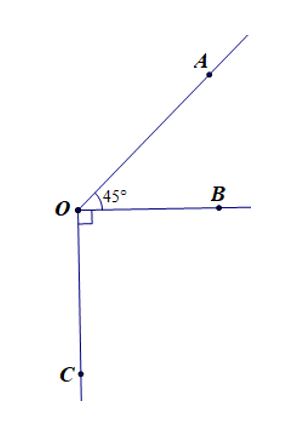
Câu 4. Cho hình vẽ
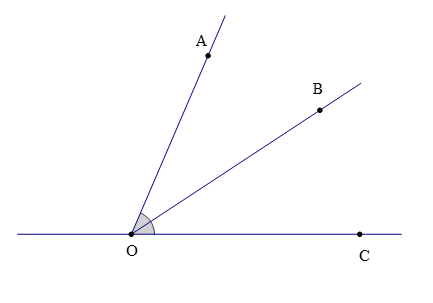
Chọn khẳng định đúng:
A. OA là tia phân giác của ;
B. OB là tia phân giác của ;
C. OC là tia phân giác của ;
D. Cả 3 phương án đều đúng.
Đáp án: B
Giải thích:
Vì tia OB nằm giữa hai tia OA và OC nên tạo thành hai góc tương ứng là và
Mà
Do đó OB là tia phân giác của
Câu 5. Tia Oz là tia phân giác của , biết rằng . Số đo của là:
A. 20°;
B. 40°;
C. 80°;
D. 140°.
Đáp án: B
Giải thích:
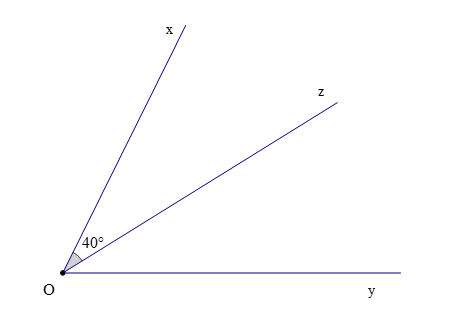
Theo bài ta có: Oz là tia phân giác của
Nên (tính chất tia phân giác của một góc)
Mà
Suy ra
Câu 6. Cho , biết rằng OE là tia phân giác của . Số đo của là
A. 20°;
B. 40°;
C. 70°;
D. 110°.
Đáp án: C
Giải thích:
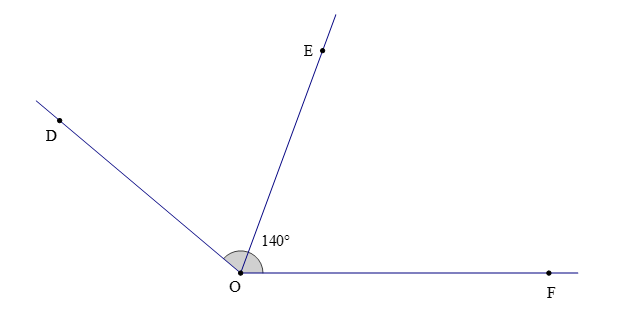
Theo bài ta có: OE là tia phân giác của
Nên (tính chất đường phân giác của một góc) (1)
Ta lại có (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Do đó
Câu 7. Cho , kẻ Oz sao cho Oy là phân giác của . Khi đó là
A. Góc nhọn;
B. Góc vuông;
C. Góc tù;
D. Góc bẹt.
Đáp án: D
Giải thích:
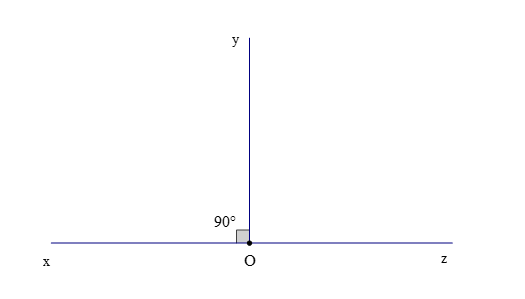
Theo bài tia Oy là phân giác của
Nên (tính chất tia phân giác của một góc)
Ta có (hai góc kề nhau)
Hay
Suy ra
Do đó là góc bẹt.
II. Thông hiểu
Câu 1. Cho hình vẽ
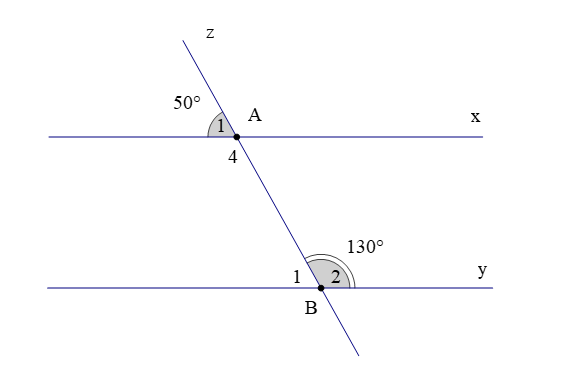
Chọn khẳng định sai:
A. x // y;
B. ;
C. ;
D.
Đáp án: D
Giải thích:
Ta có (hai góc kề bù)
Hay
Suy ra nên phương án B đúng.
Ta lại có (hai góc kề bù)
Hay
Suy ra nên phương án C đúng.
Vì (cùng bằng 50°)
Mà và nằm ở vị trí đồng vị
Do đó x // y nên A đúng.
Ta có (hai góc đối đỉnh)
Do đó nên D sai.
Câu 2. Cho hình vẽ
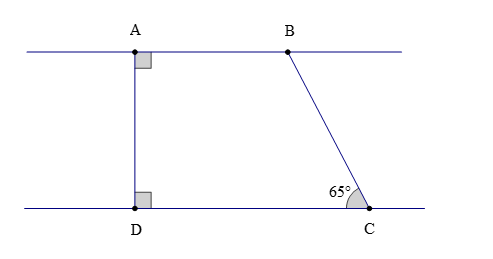
Số đo của là:
A. 65°;
B. 80°;
C. 115°;
D. 130°.
Đáp án: C
Giải thích:
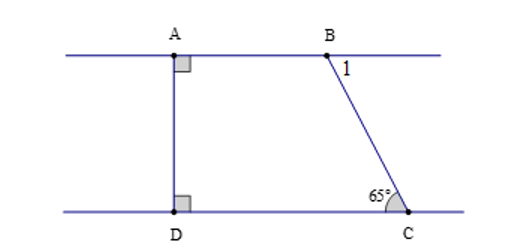
Ta có: AB ⊥ AD và DC ⊥ AD.
Suy ra AB // CD (hai đường thẳng phân biệt cũng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau).
Do đó (hai góc so le trong)
Nên
Mà (hai góc kề bù)
Hay
Suy ra
Câu 3. Một định lí được minh họa bởi hình vẽ:
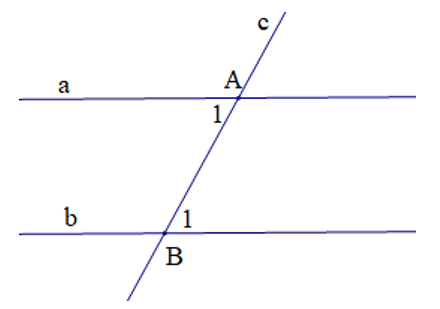
Định lí có giả thiết và kết luận như sau:
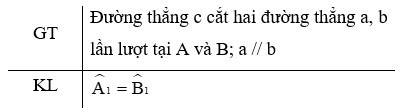
Định lí được phát biểu thành lời là:
A. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc bất kì bằng nhau;
B. Nếu hai đường thẳng cắt một đường thẳng thứ ba và trong các góc tạo thành có một cặp góc so le trong bằng nhau nhau thì hai đường thẳng đó song song;
C. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau;
D. Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có tổng bằng 180°.
Đáp án: C
Giải thích:
Từ giả thiết và kết luận ta có: Nếu đường thẳng c cắt hai đường thẳng song song a và b lần lượt tại hai điểm A và B thì hai góc so le trong và ![]() bằng nhau.
bằng nhau.
Một cách tổng quát ta có định lí: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Câu 4. Cho hình vẽ, biết rằng OB là tia phân giác của .
Số đo của là
A. 30°;
B. 31°;
C. 32°;
D. 33°.
Đáp án: B
Giải thích:
Ta có và là hai góc kề bù nên
Hay
Suy ra
Theo bài ta có OB là tia phân giác của
Do đó (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Hay
Câu 5. Cho hình vẽ, biết rằng và Oz là phân giác của .
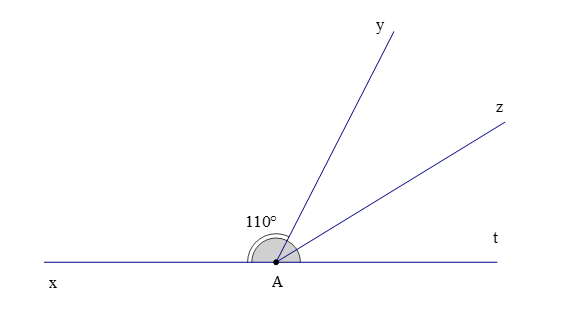
Số đo của là
A. 35°;
B. 70°;
C. 110°;
D. 145°.
Đáp án: D
Giải thích:
Ta có (hai góc kề bù)
Hay
Suy ra
Theo bài ta có Oz là phân giác của
Suy ra (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Ta có (hai góc kề nhau)
Hay
Suy ra
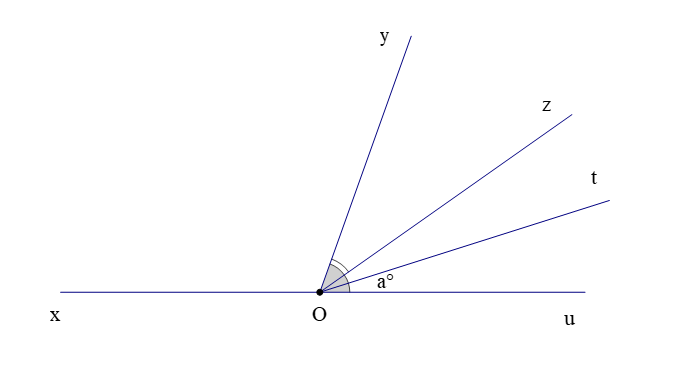
Câu 6. Cho hình vẽ
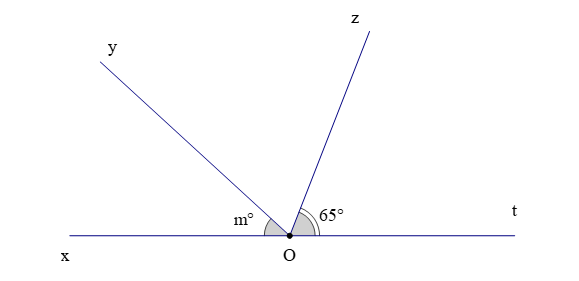
Giá trị của m để tia Oz là tia phân giác của là:
A. m = 50;
B. m = 55;
C. m = 60;
D. m = 65.
Đáp án: A
Giải thích:
Để tia Oz là tia phân giác của thì (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Suy ra
Ta lại có (hai góc kề bù)
Suy ra
Do đó m = 50
Câu 7. Cho hình vẽ:
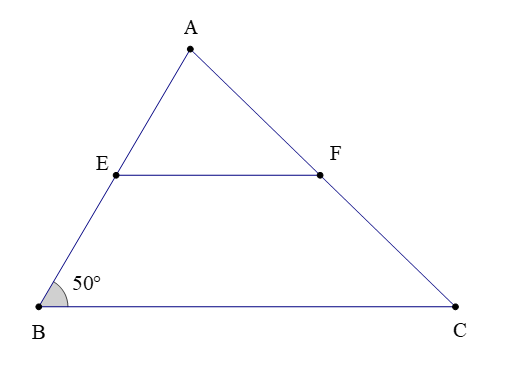
Biết rằng EF // BC. Số đo của là:
A. 25°;
B. 155°;
C. 50°;
D. 130°.
Đáp án: D
Giải thích:
Theo bài ta có EF // BC (1)
Mà và là hai góc nằm ở vị trí đồng vị (2)
Từ (1) và (2) suy ra (tính chất hai đường thẳng song song).
Lại có (hai góc kề bù)
Suy ra
Hay
Câu 8. Cho hình vẽ. Biết rằng x // y; đường thẳng z cắt hai đường thẳng x, y lần lượt tại A, B sao cho .
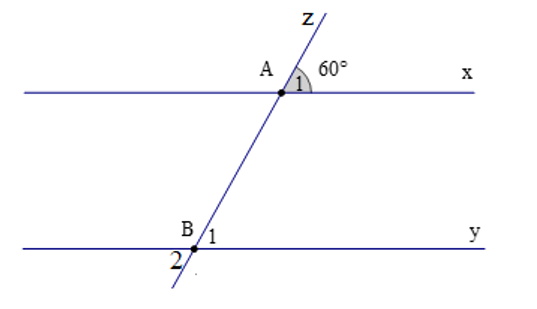
Số đó của là:
A. 60°;
B. 120°;
C. 30°;
D. 90°.
Đáp án: A
Giải thích:
Vì x // y nên (hai góc đồng vị)
Ta có (hai góc đối đỉnh)
Suy ra
III. Vận dụng
Câu 1. Cho hình vẽ.
Kẻ tia OE là tia đối của tia OB và tia OD nằm giữa hai tia OC và OE sao cho Chọn khẳng định sai:
A. và là hai góc bù nhau;
B. và là hai góc kề bù;
C. và là hai góc đối đỉnh;
D. và là hai góc đối đỉnh.
Đáp án: C
Giải thích:
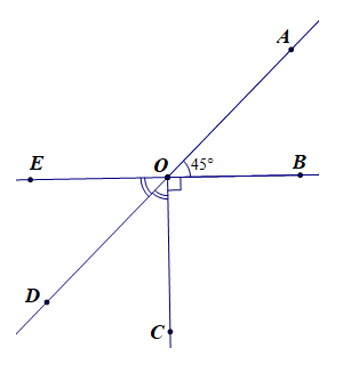
Theo bài ta có: CO ⊥ OB mà OE là tia đối của OB.
Do đó CO ⊥ EB
Suy ra
Theo bài và (hai góc kề nhau)
Suy ra
Ta có
Hay
Suy ra và là hai góc bù nhau (vì hai góc bù nhau có tổng số đo bằng 180°) nên A đúng.
• Ta lại có và có chung cạnh OB và không có điểm trong chung nên hai góc và là hai góc kề nhau.
Vì hai góc và vừa kề nhau và vừa bù nhau nên và là hai góc kề bù. Do đó B đúng.
• Ta có (chứng minh trên)
Hay suy ra OA và OD là hai tia đối nhau.
Mà OB và OE là hai tia đối nhau (giả thiết).
Do đó hai góc và là hai góc đối đỉnh nên D đúng.
• Ta có ;
OA và OD là hai tia đối nhau nhưng OB và OC không phải là hai tia đối nhau.
Do đó và không là hai góc đối đỉnh nên C sai.
Câu 2. Cho hình vẽ, biết rằng OC là tia phân giác của và .
Số đo của là
A. 70°;
B. 71°;
C. 72°;
D. 73°.
Đáp án: C
Giải thích:
Ta có (hai góc kề bù) (1)
Mà (giả thiết) (2)
Thay (2) vào (1) ta có:
Hay
Do đó
Thay vào (2) ta có:
Theo bài tia OC là tia phân giác của
Do đó (tính chất tia phân giác của một góc) (3)
Mà (hai góc kề nhau) (4)
Từ (3) và (4) suy ra
Câu 3. Cho hình vẽ, biết rằng Oz, Ot lần lượt là tia phân giác của và và
Chọn khẳng định đúng:
A. ;
B. ;
C. ;
D. .
Đáp án: D
Giải thích:
Theo bài ra ta có Ot là tia phân giác của
Suy ra (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Do đó
Ta lại có Oz là tia phân giác của
Suy ra (tính chất tia phân giác của một góc) (3)
Mà (hai góc kề nhau) (4)
Từ (3) và (4) suy ra
Do đó
Mà
Do đó
Ta có (hai góc kề bù)
Hay
Suy ra
Câu 4. Cho hình vẽ
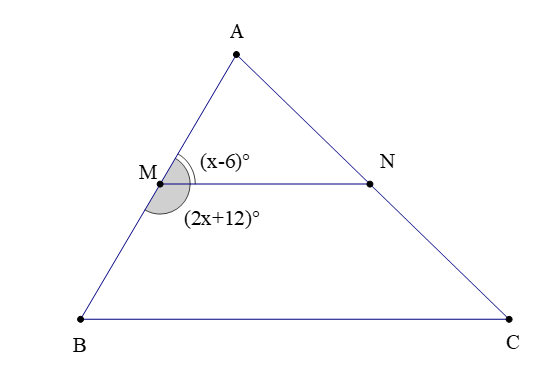
Biết rằng MN // BC. Số đó của là:
A. 52°;
B. 54°;
C. 56°;
D. 58°.
Đáp án: A
Giải thích:
Ta có (hai góc kề bù)
Nên (x – 6)° + (2x + 12)° = 180°
Do đó (x – 6 + 2x + 12)° = 180°
Suy ra x – 6 + 2x + 12 = 180
Hay 3x = 180 + 6 – 12 = 174
Suy x = 58
Do đó
Vì MN // BC nên (hai góc đồng vị)
Hay
Câu 5. Cho hình vẽ:
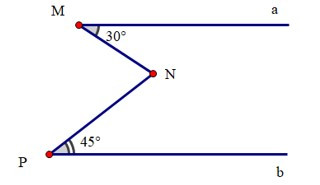
Biết Ma // Pb. Số đo là:
A. 30°;
B. 45°;
C. 75°;
D. 105°.
Đáp án: C
Giải thích:
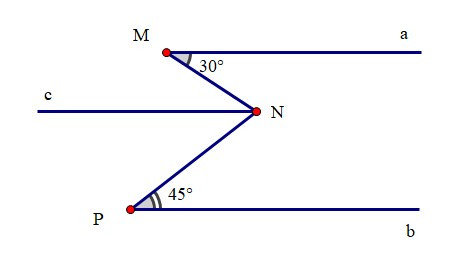
Kẻ Nc // Ma.
Suy ra (hai góc so le trong)
Ta có Nc // Ma, mà Ma // Pb
Suy ra Pb // Nc (vì cùng song song với Ma)
Suy ra (hai góc so le trong)
Ta có (hai góc kề bù)
Do đó = 30° + 45° = 75°.
Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 4. Định lí và chứng minh một định lí
Trắc nghiệm Bài 1. Thu thập và phân loại dữ liệu