Tailieumoi.vn xin giới thiệu Trắc nghiệm Toán lớp 7 Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác sách Chân trời sáng tạo. Bài viết gồm 20 câu hỏi trắc nghiệm với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài trắc nghiệm Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác. Mời các bạn đón xem:
Trắc nghiệm Toán 7 Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
I. Nhận biết
Câu 1. Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
A. 6;
B. 9;
C. 12;
D. 16.
Đáp án: B
Giải thích:
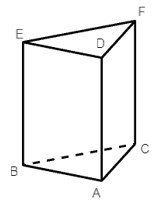
Các cạnh của hình lăng trụ đứng tam giác ABC.DEF là: AB, BC, CA, DE, EF, FD, AD, BE, CF.
Vậy hình lăng trụ đứng tam giác có 9 cạnh.
Câu 2. Quan sát hình lăng trụ đứng tứ giác sau:
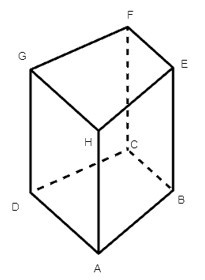
Khẳng định nào sau đây là đúng?
A. EB = HA = GD = FC;
B. EB = HE = FG = CD;
C. EB = CB = DA = GH;
D. EB = AC = FH.
Đáp án: A
Giải thích:
Theo hình vẽ ta thấy EB, HA, GD, FC là chiều cao của hình lăng trụ đứng.
Do đó EB = HA = GD = FC.
Câu 3. Mặt nào sau đây là mặt bên của hình lăng trụ đứng ABCD.HEFG?
A. ABEH;
B. BCFE;
C. ADGH;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
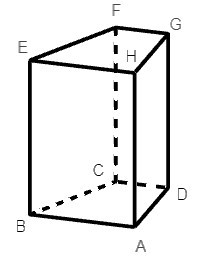
Hình lăng trụ đứng ABCABCD.HEFG có 4 mặt bên là: ABEH; BCFE; ADGH;CDGF.
Do đó ba đáp án A, B, C đều đúng.
Câu 4. Các cạnh bên của hình lăng trụ đứng:
A. Song song với nhau;
B. Bằng nhau;
C. Vuông góc với hai đáy;
D. Có cả ba tính chất ở đáp án A, B, C.
Đáp án: D
Giải thích:
Hình lăng trụ đứng có các cạnh bên của hình lăng trụ đứng song song, bằng nhau và vuông góc với mặt đáy.
Do đó A, B, C đều đúng.
Câu 5. Các mặt bên của hình lăng trụ đứng là
A. Hình thoi;
B. Hình tam giác;
C. Hình bình hành;
D. Hình chữ nhật.
Đáp án: D
Giải thích:
Hình lăng trụ có hai đáy là những đa giác và các mặt bên là những hình chữ nhật.
II. Thông hiểu
Câu 1. Cho một hình lăng trụ đứng có tổng 12 cạnh. Hỏi đáy của hình lăng trụ đứng này không thể là hình gì?
A. Hình vuông;
B. Hình chữ nhật;
C. Hình tam giác;
D. Hình thoi.
Đáp án: D
Giải thích:
Hình lăng trụ đứng có 12 cạnh nên hình lăng trụ này là hình lăng trụ đứng tứ giác.
Do đó đáy của hình lăng trụ là một hình tứ giác, có thể là hình vuông hoặc hình chữ nhật, hình thoi.
Câu 2. Cho lăng trụ đứng tứ giác ABCD.EFGH, biết CD = 4 cm và diện tích của mặt CDHG bằng 36 cm2. Chiều cao của lăng trụ là:
A. 32 cm;
B. 9 cm;
C. 40 cm;
D. 10 cm.
Đáp án: B
Giải thích:
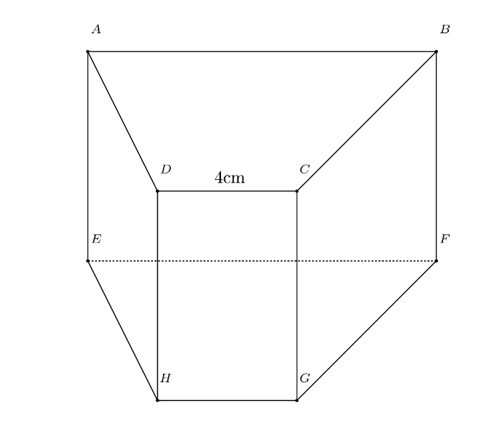
Vì ABCD.EFGH là lăng trụ đứng tứ giác nên mặt bên CDHG là hình chữ nhật.
Do đó SCDHG = CD. DH = 36 cm2
Mà CD = 4 cm nên DH = SCDHG : CD = 36 : 4 = 9 (cm).
Chiều cao của hình lăng trụ đứng là độ dài một cạnh bên, mà DH là cạnh bên của hình lăng trụ này.
Vậy chiều cao của lăng trụ đứng ABCD.EFGH là 9 cm.
Câu 3. Một hình lăng trụ đứng có tất cả 5 mặt. Hình lăng trụ này có bao nhiêu đỉnh?
A. 5 đỉnh;
B. 6 đỉnh;
C. 8 đỉnh;
D. 10 đỉnh.
Đáp án: B
Giải thích:
Hình lăng trụ đứng có tất cả 5 mặt nên đây là hình lăng trụ đứng tam giác.
Hình lăng trụ đứng tam giác có tất cả 6 đỉnh.
Câu 4. Hình lăng trụ đứng tứ giác có:
(1) Các mặt đáy song song với nhau;
(2) Các mặt đáy là tam giác;
(3) Các mặt đáy là tứ giác;
(4) Các mặt bên là hình chữ nhật.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
Hình lăng trụ đứng tứ giác có các mặt đáy là tứ giác và song song với nhau, các mặt bên là các hình chữ nhật.
Do đó (1) (3) (4) đúng.
Vậy có 3 khẳng định đúng.
Câu 5. Cho hình lăng trụ đứng ABCD.EHGF có đáy ABCD là hình thang cân (AB // CD). Có bao nhiêu cạnh có độ dài bằng với độ dài cạnh GH?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
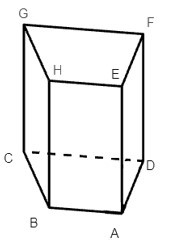
Do ABCD là hình thang cân nên ta có AD = BC (1)
Do ABCD.EHGF là hình lăng trụ đứng nên các mặt bên là hình chữ nhật.
• AEFD là hình chữ nhật nên AD = EF (2)
• BCGH là hình chữ nhật nên BC = GH (3)
Từ (1), (2) và (3) ta có AD = BC = EF = GH.
Vậy có 3 cạnh có độ dài bằng với cạnh GH.
Câu 6. Cho hình lăng trụ đứng sau:
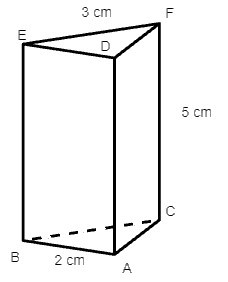
Độ dài của các cạnh ED, BC, DA lần lượt bằng
A. 2 cm, 3 cm, 5 cm;
B. 5 cm, 3 cm, 2 cm;
C. 2 cm, 5 cm, 3 cm;
D. 3 cm, 2 cm, 5 cm.
Đáp án: A
Giải thích:
Vì ABC.DEF là hình lăng trụ đứng tam giác nên các mặt bên là hình chữ nhật.
Do đó:
ED = BA = 2 cm; BC = EF = 3 cm; DA = FC = 5 cm.
Câu 7. Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông Có bao nhiêu góc vuông tại đỉnh A thuộc các mặt của lăng trụ?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: D
Giải thích:
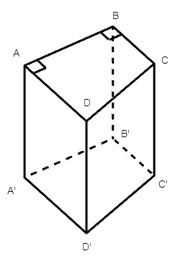
Do ABCD là hình thang vuông nên ta có
Mặt khác ta có hình lăng trụ đứng ABCD.A'B'C'D' nên ta có: .
Vậy có ba góc vuông tại đỉnh A thuộc các mặt của lăng trụ đứng là
III. Vận dụng
Câu 1. Phải gấp các cạnh nào của hình sau đây với nhau để được một hình lăng trụ đứng tam giác?
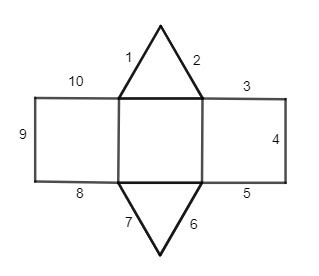
A. 1 và 10, 2 và 3, 8 và 4, 9 và 7, 5 và 6;
B. 1 và 10, 2 và 3, 9 và 4, 8 và 7, 5 và 6;
C. 1 và 10, 2 và 4, 9 và 3, 8 và 7, 5 và 6;
D. 1 và 10, 2 và 3, 9 và 5, 8 và 7, 4 và 6.
Đáp án: B
Giải thích:
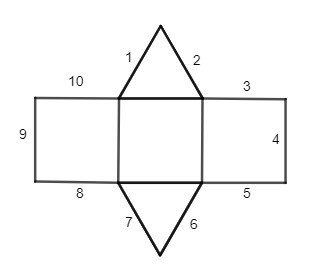
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lăng trụ đứng tam giác: 1 và 10, 2 và 3, 9 và 4, 8 và 7, 5 và 6.
Khi đó ta sẽ được hình sau:
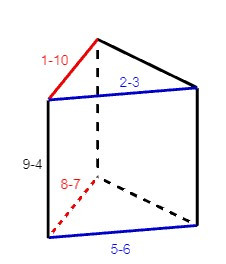
Câu 2. Phải gấp các cạnh nào của hình sau đây với nhau để được một hình lăng trụ đứng tứ giác? Cho biết chiều cao của tứ giác đó.
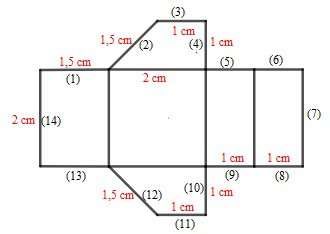
A. 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 2 cm;
B. 4 và 5, 3 và 6, 7 và 1, 14 và 2, 11 và 3, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 2 cm;
C. 4 và 5, 3 và 6, 7 và 1, 14 và 2, 11 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 1 cm;
D. 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10. Hình lăng trụ đứng có chiều cao là 1 cm.
Đáp án: A
Giải thích:
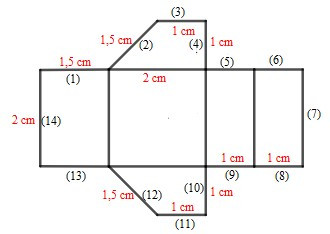
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lăng trụ đứng tứ giác: 4 và 5, 3 và 6, 2 và 1, 14 và 7, 12 và 13, 11 và 8, 9 và 10.
Khi đó ta có hình sau:
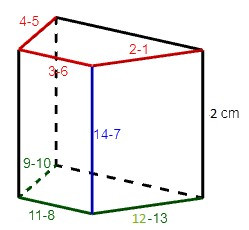
Ta có chiều cao của hình lăng trụ đứng này là: 2 cm.
Câu 3. Phương pháp đơn giản nhất để tạo một hình lăng trụ đứng tam giác từ hình sau là
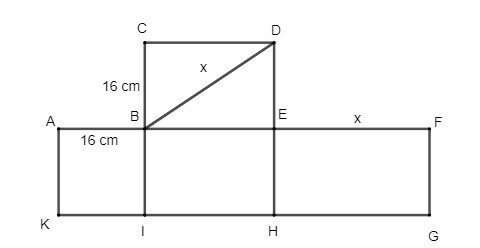
A. Cắt theo đoạn thẳng CE;
B. Cắt theo đoạn thẳng BD;
C. Cắt theo cạnh BE;
D. Cả A và B đều đúng.
Đáp án: A
Giải thích:
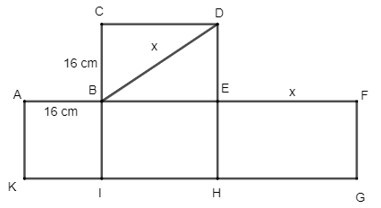
Phương pháp đơn giản nhất để tạo hình lăng trụ tam giác từ hình trên là:
Bước 1: Cắt theo cạnh CE khi đó ta có hình sau:
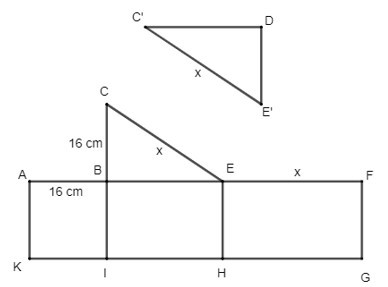
Bước 2: Ghép các cạnh sau với nhau: AK và FG; CB và AB; CE và EF, KI và DE'; DC' và IH; C'E' và HG.
Ta được hình lăng trụ đứng sau:
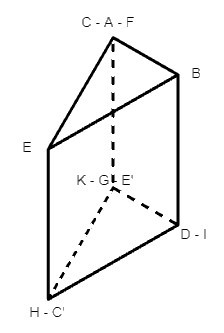
Vậy phương pháp đơn giản nhất để tạo một hình lăng trụ đứng tam giác từ hình đã cho là: Cắt theo đoạn thẳng CE.
Tương tự với cạnh BC.
Xem thêm các bài trắc nghiệm Toán 7 Chân trời sáng tạo hay, chi tiết khác:
Trắc nghiệm Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương
Trắc nghiệm Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác