Với tóm tắt lý thuyết Toán lớp 10 Bài 2: Giải bất phương trình bậc hai một ẩn sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 10.

Lý thuyết Toán lớp 10 Bài 2: Giải bất phương trình bậc hai một ẩn

A. Lý thuyết Giải bất phương trình bậc hai một ẩn

– Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng:

ax² + bx + c ≤ 0, ax² + bx + c < 0, ax² + bx + c ≥ 0, ax² + bx + c > 0, với a ≠ 0.

Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình ta được bất đẳng thức đúng.

Ví dụ: Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, x = –2 và x = 3 có phải là nghiệm của bất phương trình đó hay không?

a) 2x² – 7x – 15 < 0;

b) 3 – 2x² + x³ > 0;

c) x² – 4x + 3 ≥ 0.

Hướng dẫn giải

a) 2x² – 7x – 15 < 0

Bất phương trình trên là bất phương trình bậc hai một ẩn dạng ax² + bx + c < 0 với a = 2, b = –7, c = –15.

• Với x = –2 thay vào bất phương trình ta có:

2.(–2)² – 7.(–2) – 15 < 0

$\iff$ 7 < 0. Đây là bất đẳng thức sai.

Do đó x = –2 không là nghiệm của bất phương trình.

• Với x = 3 thay vào bất phương trình ta có:

2.3² – 7.3 – 15 < 0

$\iff$ –18 < 0. Đây là bất đẳng thức đúng.

Do đó x = 3 là nghiệm của bất phương trình.

b) 3 – 2x² + x³ > 0

Bất phương trình trên không là bất phương trình bậc hai một ẩn vì có chứa x³.

c) x² – 4x + 3 ≥ 0.

Bất phương trình trên là bất phương trình bậc hai một ẩn dạng ax² + bx + c ≥ 0 với a = 1, b = –4, c = 3.

• Với x = –2 thay vào bất phương trình ta có:

(–2)² – 4.(–2) + 3 ≥ 0

$\iff$ 15 ≥ 0. Đây là bất đẳng thức đúng.

Do đó x = –2 là nghiệm của bất phương trình.

• Với x = 3 thay vào bất phương trình ta có:

3² – 4.3 + 3 ≥ 0

$\iff$ 0 ≥ 0. Đây là bất đẳng thức đúng.

Do đó x = 3 là nghiệm của bất phương trình.

– Giải bất phương trình bậc hai là tìm tập hợp các nghiệm của bất phương trình đó.

Ta có thể giải bất phương trình bậc hai bằng cách xét dấu của tam thức bậc hai tương ứng.

Ví dụ: Giải các bất phương trình sau:

a) x² – 3x + 2 < 0;

b) –2x² + 3x – 7 ≥ 0.

Hướng dẫn giải

a) x² – 3x + 2 < 0

Xét tam thức bậc hai f(x) = x² – 3x + 2

Ta có ∆ = (–3)² – 4.1.2 = 1 > 0

Do đó f(x) có hai nghiệm phân biệt là x₁ = 1 và x₂ = 2.

Vì a = 1 > 0 nên ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu f(x) < 0 $\iff$ x ∈ (1; 2).

Vậy bất phương trình đã cho có tập nghiệm là (1; 2).

b) –2x² + 3x – 7 ≥ 0.

Xét tam thức bậc hai f(x) = –2x² + 3x – 7

Ta có ∆ = 3² – 4.(–2).(–7) = –47 < 0.

Mặt khác a = –2 < 0

Do đó f(x) < 0 với mọi x.

Khi đó không có giá trị nào của x thỏa mãn f(x) ≥ 0.

Vậy bất phương trình đã cho vô nghiệm.

B. Bài tập tự luyện

Bài 1. Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau:

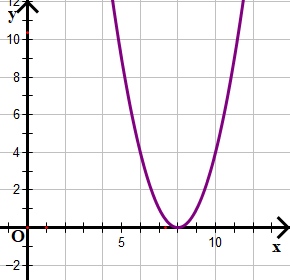
a) x² – 16x + 64 > 0

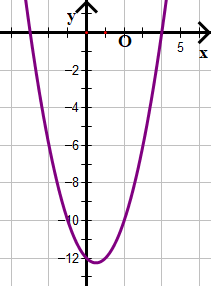
b) x² – x – 12 ≥ 0

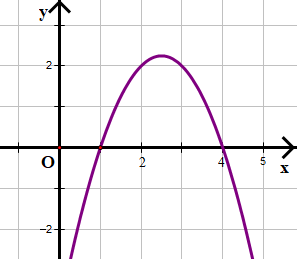
c) –x² + 5x – 4 < 0

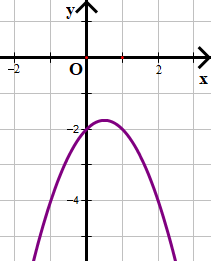
d) –x² + x – 2 ≥ 0

Hướng dẫn giải

a) x² – 16x + 64 > 0

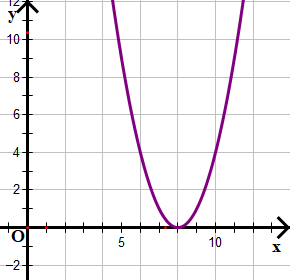
Xét tam thức bậc hai f(x) = x² – 16x + 64

Dựa vào đồ thị ta thấy f(x) nằm trên trục hoành và cắt trục hoành tại điểm có hoành độ x = 8.

Do đó f(x) ≥ 0 với mọi x.

Khi đó f(x) > 0 $\iff$ x ≠ 8.

Vậy tập nghiệm của bất phương trình là ℝ \ {8}.

b) x² – x – 12 ≥ 0

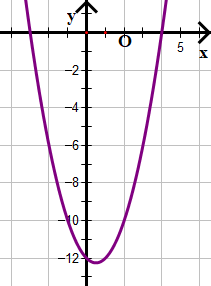
Xét tam thức bậc hai f(x) = x² – x – 12

Dựa vào đồ thị ta thấy đồ thị cắt trục hoành tại hai điểm có hoành độ là x₁ = –3 và x₂ = 4.

Đồ thị f(x) nằm trên trục hoành khi x nằm trong khoảng (–∞; –3) và (4; +∞).

Do đó f(x) ≥ 0 $\iff$ x ≤ –3 hoặc x ≥ 4.

Vậy bất phương trình đã cho có tập nghiệm là (–∞; –3) ∪ (4; +∞).

c) –x² + 5x – 4 < 0

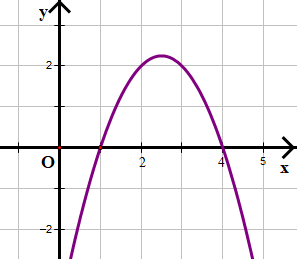
Xét tam thức bậc hai f(x) = –x² + 5x – 4

Dựa vào đồ thị hàm số ta thấy đồ thị cắt trục hoành tại hai điểm có hoành độ x₁ = 1 và x₂ = 4.

Đồ thị f(x) nằm dưới trục hoành khi x nằm trong khoảng (1; 4).

Do đó f(x) < 0 $\iff$ x ∈ (1; 4).

Vậy bất phương trình đã cho có tập nghiệm là (1; 4).

d) –x² + x – 2 ≥ 0

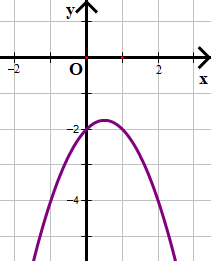
Xét tam thức bậc hai f(x) = –x² + x – 2

Dựa vào đồ thị hàm số ta thấy đồ thị nằm hoàn toàn dưới trục hoành.

Do đó f(x) < 0 với mọi x.

Khi đó bất phương trình f(x) ≥ 0 $\iff$ x ∈ ∅.

Vậy bất phương trình có tập nghiệm là ∅.

Bài 2. Giải các bất phương trình bậc hai sau:

a) 6x² + x – 1 ≤ 0;

b) –x² – x – 1 > 0;

c) –2x² < 2x – 5;

d) –x² ≥ 2x + 1;

e) x² + 2x – 7 ≤ 2x² – 2x.

Hướng dẫn giải

a) 6x² + x – 1 ≤ 0

Xét tam thức bậc hai f(x) = 6x² + x – 1 có a = 6 > 0.

Ta có: ∆ = 1² – 4.6.(–1) = 25 > 0

Do đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-1+\sqrt{25}}{2.6}=\frac{1}{3}$ và  $x_2=\frac{-1-\sqrt{25}}{2.6}=\frac{-1}{2}$

Ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu ta có:

f(x) ≤ 0 $\iff$  $\frac{-1}{2}\le x\le \frac{1}{3}.$

Vậy bất phương trình đã cho có tập nghiệm là $\left[\frac{-1}{2};\frac{1}{3}\right].$

b) –x² – x – 1 > 0

Xét tam thức bậc hai f(x) = –x² – x – 1 có a = –1 < 0.

Ta có: ∆ = (–1)² – 4.(–1).(–1) = –3 < 0.

Do đó f(x) vô nghiệm nên f(x) < 0 với mọi x.

Khi đó không có giá trị nào của x thỏa mãn f(x) > 0.

Vậy bất phương trình đã cho có tập nghiệm là ∅.

c) –2x² < 2x – 5

$\Rightarrow$ –2x² – 2x + 5 < 0

Xét tam thức bậc hai f(x) = –2x² – 2x + 5 có a = –2 < 0.

Ta có: ∆' = (–1)² – (–2).5 = 11 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{1+\sqrt{11}}{-2}=\frac{-1-\sqrt{11}}{2}$ và  $x_2=\frac{1-\sqrt{11}}{-2}=\frac{-1+\sqrt{11}}{2}$

Ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu ta có:

f(x) < 0 $\iff$ $x<\frac{-1-\sqrt{11}}{2}$ hoặc $x>\frac{-1+\sqrt{11}}{2}.$

Vậy bất phương trình đã cho có tập nghiệm là $\left(-\infty ;\frac{-1-\sqrt{11}}{2}\right)\cup \left(\frac{-1+\sqrt{11}}{2};+\infty \right).$

d) –x² ≥ 2x + 1

$\Rightarrow$ –x² – 2x – 1 ≥ 0.

Xét tam thức bậc hai f(x) = –x² – 2x – 1 có a = –1 < 0.

Ta có: D' = (–1)² – (–1).(–1) = 0.

Do đó f(x) có nghiệm kép x = –1.

Ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu ta có:

f(x) ≥ 0 Û x = –1.

Vậy bất phương trình đã cho có tập nghiệm {–1}.

e) x² + 2x – 7 ≤ 2x² – 2x.

$\Rightarrow$ x² + 2x – 7 – 2x² + 2x ≤ 0

$\Rightarrow$ –x² + 4x – 7 ≤ 0.

Xét tam thức bậc hai f(x) = –x² + 4x – 7 có a = –1 < 0.

Ta có: ∆' = 2² – (–1).(–7) = –3 < 0.

Do đó f(x) < 0 với mọi x.

Khi đó f(x) ≤ 0 với mọi x.

Vậy bất phương trình đã cho có tập nghiệm là ℝ.

Bài 3. Một quả bóng được ném thẳng từ độ cao 1,5 mét với vận tốc ban đầu 10 m/s. Độ cao của bóng so với mặt đất (m) sau t (giây) được cho bởi hàm số h(t) = –5t² + 10t + 1,5. Quả bóng có thể đạt được độ cao trên 5 m không? Nếu có thì trong bao lâu? Làm tròn kết quả đến hàng phần mười.

Hướng dẫn giải

Để quả bóng có thể đạt được độ cao trên 5 m thì h(t) = –5t² + 10t + 1,5 > 5.

$\Rightarrow$ –5t² + 10t – 3,5 > 0.

$\Rightarrow$ t² – 2t + 0,7 < 0.

Xét tam thức bậc hai f(x) = t² – 2t + 0,7 có a = 1 > 0.

Ta có D' = (–1)² – 1.0,7 = 0,3 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$t_1=\frac{1+\sqrt{0,3}}{1}\approx 1,5$ và $t_2=\frac{1-\sqrt{0,3}}{1}\approx 0,5$

Ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu ta có:

f(t) < 0 $\iff$ t ∈ (0,5; 1,5).

Vậy quả bóng có thể đạt được độ cao trên 5 m trong khoảng từ 0,5 giây cho đến 1,5 giây.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Dấu của tam thức bậc hai

Lý thuyết Bài 2: Giải bất phương trình bậc hai một ẩn

Lý thuyết Bài 3: Phương trình quy về phương trình bậc hai

Lý thuyết Bài 1: Quy tắc cộng và quy tắc nhân

Lý thuyết Bài 2: Hoán vị, chỉnh hợp và tổ hợp