Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 8 Bài 6: Đối xứng trục chọn lọc, có đáp án. Tài liệu gồm 20 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 8. Hi vọng với bộ câu hỏi trắc nghiệm Đối xứng trục có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi môn Toán 8.
Giới thiệu về tài liệu:
- Số câu hỏi trắc nghiệm: 20 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Đối xứng trục có đáp án - Toán lớp 8:

Trắc nghiệm Toán 8
Bài 6: Đối xứng trục
Bài 1: Cho tam giác ABC cân tại A, các đường trung tuyến AA’, BB’, CC’. Trục đối xứng của tam giác ABC là:
A. AA’
B. BB’
C. AA’ và CC’
D. CC’
Lời giải
Do tam giác ABC cân tại A, nên đường trung tuyến AA’ đồng thời là đường trung trực.
Do đó AA’ là trục đối xứng của tam giác ABC.
Đáp án cần chọn là: A
Bài 2: Hãy chọn câu sai:
A. Nếu hai góc đối xứng nhau qua một đường thẳng thì chúng bằng nhau
B. Nếu hai tam giác đối xứng nhau qua một đường thẳng thì chúng bằng nhau
C. Nếu hai tam giác đối xứng nhau qua một đường thẳng thì chu vi của chúng bằng nhau.
D. Nếu hai tia đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Lời giải
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau nên D sai.
Đáp án cần chọn là: D
Bài 3: Cho hình vẽ. Hãy chọn câu đúng:
A. Điểm đối xứng với A qua đường thẳng d là A.
B. Điểm đối xứng với K qua đường thẳng d là K
C. Điểm đối xứng với A qua đường thẳng d là K
D. Điểm đối xứng với Q qua đường thẳng d là Q.
Lời giải
Từ hình vẽ ta có đường thẳng d là đường trung trực của đoạn thẳng AK nên điểm đối xứng với A qua đường thẳng d là K.
Đáp án cần chọn là: C
Bài 4: Cho hình vẽ. Hãy chọn câu sai.
A. Điểm đói xứng với P qua đường thẳng QG là P’.
B. Điểm đối xứng với B qua đường thẳng QG là B’.
C. Điểm đối xứng với D qua đường thẳng QG là G.
D. Điểm đối xứng với G qua đường thẳng QG là G
Lời giải
Từ hình vẽ ta có đường thẳng QG là đường trung trực của đoạn thẳng DD’, BB’, PP’ nên
Điểm đối xứng với P qua đường thẳng QG là P’ nên B đúng.
ĐIểm đối xứng với B qua đường thẳng QG là B’ nên B đúng.
Điểm đối xứng với D qua đường thẳng QG là D’ nên C sai.
Vì G Є QG nên điểm đối xứng với G qua QG là G nên D đúng.
Đáp án cần chọn là: C
Bài 5: Hãy chọn câu sai.
A. Hai đoạn thẳng EB và E’B’ đối xứng nhau qua m.
B. Hai đoạn thẳng DB và D’B’ đối xứng nhau qua m.
C. Hai tam giác DEB và D’E’B’ đối xứng nhau qua m
D. Hai đoạn thẳng DE và D’B’ đối xứng nhau qua m.
Lời giải
Từ hình vẽ ta có A và A’ đối xứng nhau qua đường thẳng m; B và B’ đối xứng nhau qua đường thẳng m; C và C’ đối xứng nhau qua đường thẳng m.
Suy ra hai đoạn thẳng EB và E’B’ đối xứng nhau qua m.
Hai đoạn thẳng DB và D’B’ đối xứng nhau qua m.
Hai tam giác DEB và D’E’B’ đối xứng nhau qua m.
Hai đoạn thẳng DE và D’E’ đối xứng nhau qua m nên D sai.
Đáp án cần chọn là: D
Bài 6: Cho tam giác ABC, trong đó AB = 11cm, AC = 15cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 52cm
B. 54cm
C. 26cm
D. 51cm
Lời giải
Gọi A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 11cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 15cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C = 11 + 15 + 11 + 15 = 52 cm
Đáp án cần chọn là: A
Bài 7: Cho tam giác ABC, trong đó AB = 8cm, AC = 10cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 38cm
B. 54cm
C. 36cm
D. 18cm
Lời giải
Gọi A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 8cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 10cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C = 8 + 10 + 8 + 10 = 36 cm
Đáp án cần chọn là: C
Bài 8: Cho hình vuông ABCD cạnh bằng a. M và N là hai điểm lưu động lần lượt trên cạnh AB và AD sao cho 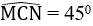
1. Chọn kết luận đúng nhất.
A. E là điểm đối xứng của N qua CM
B. Tam giác CEN là tam giác cân tại C
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Suy ra ΔCDN = ΔCBE (g.c.g)
Suy ra CN = CE
Xét tam giác CEN có CN = CE (cmt) nên tam giác CEN là tam giác cân tại C
Suy ra phân giác CM đồng thời là đường trung trực của NE.
Vậy E là điểm đối xứng của N qua CM
Đáp án cần chọn là: C
2. Tính chu vi của tam giác AMN theo a.
A. 4a
B. 3a
C. a
D. 2a
Lời giải
Ta có: ΔCMN = ΔCME (do tính đối xứng qua CM)
Nên MN = ME
Suy ra chu vi tam giác AMN là:
AM + AN + MN = AM + AN + ME
= AM + AN + MB + BE = AM + AN + MB + ND (vì ΔCDN = ΔCBE (theo câu trước) nên BE = ND)
= (AM + MB) + (AN + ND)
Vậy chu vi tam giác AMN bằng 2a.
Đáp án cần chọn là: D
Bài 9: Cho hai điểm A, B nằm trên cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi B’ là điểm đối xứng của B qua đường thẳng d. Tìm trên đường thẳng d điểm M sao cho tổng MA + MB nhỏ nhất. Chọn khẳng định đúng nhất.
A. M là giao điểm của đoạn thẳng AB và đoạn thẳng d.
B. M là giao điểm của đoạn AB’ và đường thẳng d.
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Lời giải
Gọi B’ là điểm đối xứng của B qua đường thẳng d. B’ cố định.
Ta có: MB = MB’ (tính chất đối xứng trục).
Xét ba điểm M, A, B’ ta có MA + MB’ ≥ AB’
Do đó MA + MB ≥ AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B thẳng hang theo thứ tự đó hay M là giao điểm của đoạn AB’ và đường thẳng d.
Vậy khi M ≡ M’ là giao điểm của đoạn thẳng AB’ và đường thẳng d thì tổng MA + MB nhỏ nhất, trong đó B’ là điểm đối xứng của B qua d.
Đáp án cần chọn là: B
Bài 10: Trên tia phân giác góc ngoài tại đỉnh C của tam giác ABC, lấy điểm M (M khác C). Chọn câu đúng.
A. MA + MB = AC + BC
B. MA + MB > AC + BC
C. MA + MB < AC + BC
D. Chưa đủ điều kiện để so sánh
Lời giải
Trên tia đối của tia CB lấy điểm A’ sao cho CA = CA’
Khi đó ta có: ΔCAA’ cân tại A có CM là phân giác góc ACA’ nên CM cũng là đường trung trực của AA’.
Từ đó ta có: MA = MA’
Nên MA + MB = MA’ + MB
Xét tam giác MA’B có MA’ +MB > A’B ⇔ MA + MB > A’C + BC
Hay MA + MB > AC + BC (vì CA = CA’)
Đáp án cần chọn là: B
Bài 11: Cho đoạn thẳng AB có độ dài 3cm và đường thẳng d. Đoạn thẳng A’B’ đối xứng với AB qua d. Độ dài đoạn thẳng A’B’ là:
A. 3cm
B. 6cm
D. 9cm
D. 12cm
Lời giải
Vì đoạn thẳng A’B’ đối xứng với AB qua d nên A’B’ = AB = 3cm.
Đáp án cần chọn là: A
Bài 12: Cho đoạn thẳng AB có độ dài 6cm và đường thẳng d. Đoạn thẳng A’B’ đối xứng với AB qua d. Độ dài đoạn thẳng A’B’ là:
A. 3cm
B. 6cm
D. 9cm
D. 12cm
Lời giải
Vì đoạn thẳng A’B’ đối xứng với AB qua d nên A’B’ = AB = 6cm.
Đáp án cần chọn là: B
Bài 13: Cho ΔABC và ΔA’B’C’ đối xứng nhau qua đường thẳng d biết AB = 4cm, BC = 7cm và chu vi của tam giác ABC = 17cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
A. 17cm
B. 6cm
C. 7cm
D. 4cm
Lời giải
+ Xét tam giác ABC có chu vi PABC = AB + AC + BC ⇒ PABC = 6cm.
+ Vì tam giác ABC và tam giác A’B’C’ đối xứng nhau qua đường thẳng d nên AC = A’C’ = 6cm
Đáp án cần chọn là: B
Bài 14: Cho ΔABC và ΔA’B’C’ đối xứng nhau qua đường thẳng d biết AB = 8cm, BC = 11cm và chu vi của tam giác ABC = 30 cm. Khi đó độ dài cạnh C’A’ của tam giác A’B’C’ là:
A. 16cm
B. 15cm
C. 8cm
D. 11cm
Lời giải
+ Xét tam giác ABC có chu vi PABC = AB + AC + BC ⇒ PABC = 11cm.
+ Vì tam giác ABC và tam giác A’B’C’ đối xứng nhau qua đường thẳng d nên AC = A’C’ = 11cm
Đáp án cần chọn là: D
Bài 15: Cho tam giác ABC, trong đó AB = 11cm, AC = 15cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 52cm
B. 54cm
C. 26cm
D. 51cm
Lời giải
Gọi A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 11cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 15cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C = 11 + 15 + 11 + 15 = 52 cm
Đáp án cần chọn là: A
Bài 16: Cho tam giác ABC, trong đó AB = 8cm, AC = 10cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
A. 38cm
B. 54cm
C. 36cm
D. 18cm
Lời giải
Gọi A’ là điểm đối xứng với A qua BC. Khi đó tam giác A’BC đối xứng với tam giác ABC qua BC.
Tứ giác tạo thành là ABCA’.
Ta có A’B = AB = 8cm (vì A’B và AB đối xứng nhau qua BC)
A’C = AC = 10cm (vì A’C và AC đối xứng nhau qua BC)
Chu vi tứ giác ABCA’ là
P = AB + AC + A’B + A’C = 8 + 10 + 8 + 10 = 36 cm
Đáp án cần chọn là: C
Bài 17: Cho hình vuông ABCD cạnh bằng a. M và N là hai điểm lưu động lần lượt trên cạnh AB và AD sao cho 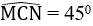
1. Chọn kết luận đúng nhất.
A. E là điểm đối xứng của N qua CM
B. Tam giác CEN là tam giác cân tại C
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Suy ra ΔCDN = ΔCBE (g.c.g)
Suy ra CN = CE
Xét tam giác CEN có CN = CE (cmt) nên tam giác CEN là tam giác cân tại C
Suy ra phân giác CM đồng thời là đường trung trực của NE.
Vậy E là điểm đối xứng của N qua CM
Đáp án cần chọn là: C
2. Tính chu vi của tam giác AMN theo a.
A. 4a
B. 3a
C. a
D. 2a
Lời giải
Ta có: ΔCMN = ΔCME (do tính đối xứng qua CM)
Nên MN = ME
Suy ra chu vi tam giác AMN là:
AM + AN + MN = AM + AN + ME
= AM + AN + MB + BE = AM + AN + MB + ND (vì ΔCDN = ΔCBE (theo câu trước) nên BE = ND)
= (AM + MB) + (AN + ND)
Vậy chu vi tam giác AMN bằng 2a.
Đáp án cần chọn là: D
Bài 18: Cho hai điểm A, B nằm trên cùng một nửa mặt phẳng bờ là đường thẳng d. Gọi B’ là điểm đối xứng của B qua đường thẳng d. Tìm trên đường thẳng d điểm M sao cho tổng MA + MB nhỏ nhất. Chọn khẳng định đúng nhất.
A. M là giao điểm của đoạn thẳng AB và đoạn thẳng d.
B. M là giao điểm của đoạn AB’ và đường thẳng d.
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Lời giải
Gọi B’ là điểm đối xứng của B qua đường thẳng d. B’ cố định.
Ta có: MB = MB’ (tính chất đối xứng trục).
Xét ba điểm M, A, B’ ta có MA + MB’ ≥ AB’
Do đó MA + MB ≥ AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B thẳng hang theo thứ tự đó hay M là giao điểm của đoạn AB’ và đường thẳng d.
Vậy khi M ≡ M’ là giao điểm của đoạn thẳng AB’ và đường thẳng d thì tổng MA + MB nhỏ nhất, trong đó B’ là điểm đối xứng của B qua d.
Đáp án cần chọn là: B
Bài 19: Trên tia phân giác góc ngoài tại đỉnh C của tam giác ABC, lấy điểm M (M khác C). Chọn câu đúng.
A. MA + MB = AC + BC
B. MA + MB > AC + BC
C. MA + MB < AC + BC
D. Chưa đủ điều kiện để so sánh
Lời giải
Trên tia đối của tia CB lấy điểm A’ sao cho CA = CA’
Khi đó ta có: ΔCAA’ cân tại A có CM là phân giác góc ACA’ nên CM cũng là đường trung trực của AA’.
Từ đó ta có: MA = MA’
Nên MA + MB = MA’ + MB
Xét tam giác MA’B có MA’ +MB > A’B ⇔ MA + MB > A’C + BC
Hay MA + MB > AC + BC (vì CA = CA’)
Đáp án cần chọn là: B
Bài 20: Cho tam giác ABC có 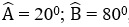
1. Tam giác M’BC là tam giác gì? Chọn đáp án đúng nhất.
A. đều
B. cân tại B
C. cân tại C
D. vuông cân tại M’
Lời giải
Do tính chất đối xứng qua d, ta có AM = BM’
Mà AM = BC (gt) nên BM’ = BC
Ta lại có: 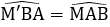
Suy ra:
Xét tam giác M’BC có BM’ = BC, 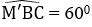
Đáp án cần chọn là: A
2. Tính góc BMC.
A. 450
B. 300
C. 600
D. 400
Lời giải
Đáp án cần chọn là: B
Bài giảng Toán 8 Bài 6: Đối xứng trục