Lời giải

Hình 1 là hình thoi vì có hai đường cheo giao nhau tại trung điểm mỗi đường và vuông góc với nhau

Hình 2 không là hình thoi vì bốn cạnh không bằng nhau

Hình 3 không là hình thoi vì bốn cạnh không bằng nhau

Đáp án cần chọn là: C

Lời giải

Tứ giác có 4 cạnh bằng nhau là hình thoi nên A đúng.

Đáp án cần chọn là: A

Lời giải

Gọi cạnh của hình thoi là a cm (a > 0)

Vì hình thoi có 4 cạnh bằng nhau nên chu vi hình thoi là 4a = 20 ⇔ a = 5cm

Vậy cạnh hình thoi có độ dài là 5cm

Đáp án cần chọn là: B

Lời giải

Gọi cạnh của hình thoi là a cm (a > 0)

Vì hình thoi có 4 cạnh bằng nhau nên chu vi hình thoi là 4a = 36 ⇔ a = 9cm

Vậy cạnh hình thoi có độ dài là 9cm

Đáp án cần chọn là: C

Lời giải

Vì chu vi hinh thoi là 16cm nên cạnh hình thoi có độ dài 16 : 4 = 4cm.

Suy ra AD = 4cm

Đáp án cần chọn là: A

Lời giải

Vì M’ đối xứng M qua D nên DM = DM’ (1)

M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình của ΔABC.

Suy ra MD // AC (2)

Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2)

Từ (1) và (2) suy ra DM ⊥ AB ⇒ MM’ ⊥ AB.

Vì D là trung điểm của AB (gt) và D là trung điểm của MM’ nên tứ giác AMBM’ là hình bình hành. Mặt khác MM’ ⊥ AB nên AMBM’ là hình thoi.

Đáp án cần chọn là: A

Lời giải

Vì BC = 4cm nên BM = 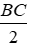 = 2cm

Chu vi tứ giác AMBM’ bằng 4.BM = 4.2 = 8cm

Đáp án cần chọn là: D

Lời giải

Gọi O là giao điểm của AC và BD thì AC ⊥ BD (do O là giao điểm của hai đường chéo của hình thoi)

Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:

Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.

Suy ra HO = OG (2)

Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)

Từ (1), (2), (3) suy ra: AHCG là hình thoi.

Đáp án cần chọn là: A

Lời giải

Vì OC = 4; OH = 3 nên 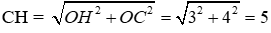 (định lý Pytago)

Vì AHCG là hình thoi (theo câu trước) nên chu vi tứ giác AHCG bằng 4.CH = 4.5 = 20cm.

Đáp án cần chọn là: A

Lời giải

Vì E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của ΔABC. Suy ra EF // AC và EF = AC. (1)

Tương tự ta có: HG // AC và HG = AC. (2)

Từ (1) và (2) suy ra tứ giác EFGH là hình bình hành.

Muốn cho tứ giác EFGH là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.

Nên EH = EF ⇔ AC = BD

Đáp án cần chọn là: A

Lời giải

Từ giả thiết ta có MP, NP, NQ, QM lần lượt là các đường trung bình của các tam giác BDE, ECD, DCB, BEC (định nghĩa đường trung bình).

Đặt BD = CE = 2a

Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:

Suy ra MN = NP = PQ = QM

Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.

Áp dụng tính chất về đường chéo vào hình thoi MNPQ ta được: MN ⊥ PQ

Đáp án cần chọn là: C

Lời giải

Từ giả thiết ta có: KM, IM, IN, KN lần lượt là các đường trung bình của các tam giác BCD, CAB, ADC, DBA (định nghĩa đường trung bình).

Đặt BA = CD = 2a.

Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:

Suy ra MK = KN = NI = IM.

Tứ giác KMIN có bốn cạnh bằng nhau nên là hình thoi.

Áp dụng tính chất về đường chéo vào hình thoi KMIN ta được: MN ⊥ KI; MN là đường phân giác 

Đáp án cần chọn là: C

Bài 11: Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Hình thang ABCD có thêm điều kiện gì thì MNPQ là hình thoi. Hãy chọn câu đúng.

A. MP = QN

B. AC ⊥ BD   

C. AB = AD   

D. AC = BD

Lời giải

+ Xét tam giác ABC có MN là đường trung bình nên MN // AC; MN = AC (1)

Tương tự ta có PQ là đường trung bình tam giác ADC nên PQ // AC; PQ = AC (2)

Từ (1) và (2) suy ra MN // PQ; MN = PQ ⇒ MNPQ là hình bình hành

Để hình bình hành MNPQ là hình thoi ta cần có MN = MQ

Mà MN = AC (cmt); MQ = BD (do MQ là đường trung bình tam giác ABD)

Suy ra AC = BD

Vậy để hình bình hành MNPQ là hình thoi thì AC = BD

Đáp án cần chọn là: D

Bài 12: Cho hình bình hành ABCD. Gọi E, F là trung điểm của các cạnh AD và BC. Các đường BE, DE cắt các đường chéo AC tại P và Q. Tứ giác EPFQ là hình thoi nếu góc ACD bằng:

A. 45⁰             

B. 90⁰             

C. 60⁰             

D. 75⁰

Lời giải

Gọi O là giao điểm của hai đường chéo AC và BD

Vì ABCD là hình bình hành nên O là trung điểm của AC, BD.

Xét tứ giác EDFB có 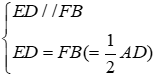  nên EDFB là hình bình hành suy ra 

Xét tam giác ABD có P là giao điểm hai đường trung tuyến nên P là trọng tâm ΔABD ⇒ EP = 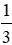BE

Xét tam giác CBD có Q là giao điểm hai đường trung tuyến nên Q là trọng tâm ΔCBD ⇒ QF = 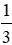DF

Mà BE = DF (cmt) ⇒ EP = QF

Xét tứ giác EPFQ có 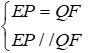 ⇒ EPQF là hình bình hành

Để hình bình hành EPFQ là hình thoi thì EF ⊥ PQ.

Mà EF // CD (do E là trung điểm AD, F là trung điểm BC)

Nên PQ ⊥ CD hay AC ⊥ CD ⇒ 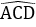  = 90⁰.

Đáp án cần chọn là: B

Bài 13: Cho hình thoi có độ dài hai đường chéo là 24cm và 10cm. Tính độ dài cạnh hình thoi.

A. 12cm         

B. 13cm          

C. 14cm          

D. 15cm

Lời giải

Giả sử ABCD là hình thoi có hai đường chéo cắt nhau tại H và AC =10cm, BD = 24cm

Do ABCD là hình thoi nên:

Xét tam giác AHB vuông tại H ta có:

AB² = AH² + HB² = 5² + 12² = 25 + 144 = 169

Suy ra AB = 13cm

Đáp án cần chọn là: B

Bài 14: Cho hình thoi có độ dài hai đường chéo là 12cm và 16cm. Tính độ dài cạnh hình thoi.

A. 12cm         

B. 8cm

C. 20cm          

D. 10cm

Lời giải

Giả sử ABCD là hình thoi có hai đường chéo cắt nhau tại H và AC =12cm, BD = 16cm

Do ABCD là hình thoi nên:

Xét tam giác AHB vuông tại H ta có:

AB² = AH² + HB² = 6² + 8² = 36 + 64 = 100

Suy ra AB = 10cm

Đáp án cần chọn là: D

Bài 15: Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D.

1. Tứ giác AMBM’ là hình gì?

A. Hình thoi   

B. Hình chữ nhật

C. Hình bình hành

D. Hình thang

Lời giải

Vì M’ đối xứng M qua D nên DM = DM’ (1)

M, D lần lượt là trung điểm của BC, AB nên MD là đường trung bình của ΔABC.

Suy ra MD // AC (2)

Mặt khác ΔABC vuông ở A nên AB ⊥ AC (2)

Từ (1) và (2) suy ra DM ⊥ AB ⇒ MM’ ⊥ AB.

Vì D là trung điểm của AB (gt) và D là trung điểm của MM’ nên tứ giác AMBM’ là hình bình hành. Mặt khác MM’ ⊥ AB nên AMBM’ là hình thoi.

Đáp án cần chọn là: A

2. Cho BC = 4cm. Tính chu vi tứ giác AMBM’.

A. 6cm

B. 9cm

C. 16cm          

D. 8cm

Lời giải

Vì BC = 4cm nên BM = 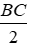 = 2cm

Chu vi tứ giác AMBM’ bằng 4.BM = 4.2 = 8cm

Đáp án cần chọn là: D

Bài 16: Cho hình thoi ABCD. Trên các cạnh BC và CD lần lượt lấy hai điểm E và F sao cho BE = DF. Gọi G, H thứu tự là giao điểm của AE, AF với đường chéo BD.

1. Tứ giác AGCH là hình gì?

A. Hình thoi   

B. Hình chữ nhật

C. Hình bình hành

D. Hình thang

Lời giải

Gọi O là giao điểm của AC và BD thì AC ⊥ BD (do O là giao điểm của hai đường chéo của hình thoi)

Áp dụng định nghĩa, tính chất về góc và giả thiết vào hình thoi ABCD, ta được:

Xét tam giác AGH có AO là đường cao, đồng thời là đường phân giác nên tam giác AGH cân tại A.

Suy ra HO = OG (2)

Do ABCD là hình thoi nên AO = OC (tính chất đường chéo của hình thoi) (3)

Từ (1), (2), (3) suy ra: AHCG là hình thoi.

Đáp án cần chọn là: A

2. Cho OC = 4; OH = 3. Tính chu vi tứ giác AHCG.

A. 20 cm        

B. 24 cm         

C. 16 cm         

D. 8 cm

Lời giải

Vì OC = 4; OH = 3 nên 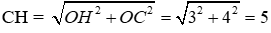 (định lý Pytago)

Vì AHCG là hình thoi (theo câu trước) nên chu vi tứ giác AHCG bằng 4.CH = 4.5 = 20cm.

Đáp án cần chọn là: A

Bài 17: Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD phải có điều kiện gì thì EFGH là hình thoi?

A. AC = BD   

B. AC ⊥ BD   

C. AB = DC   

D. AB // DC

Lời giải

Vì E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của ΔABC. Suy ra EF // AC và EF = AC. (1)

Tương tự ta có: HG // AC và HG = AC. (2)

Từ (1) và (2) suy ra tứ giác EFGH là hình bình hành.

Muốn cho tứ giác EFGH là hình thoi thì nó cần phải có thêm hai cạnh kề bằng nhau.

Nên EH = EF ⇔ AC = BD

Đáp án cần chọn là: A

Bài 18: Cho tam giác ABCD. Trên các cạnh AB và AC lần lượt lấy hai điểm D và E sao cho BD = CE. Gọi M, N, P, Q thứ tự là trung điểm của BE, CD, DE và BC. Chọn câu đúng nhất.

A. PQ vuông góc với MN      

B. Tứ giác PMQN là hình thoi

C. Cả A, B đều đúng              

D. Cả A, B đều sai

Lời giải

Từ giả thiết ta có MP, NP, NQ, QM lần lượt là các đường trung bình của các tam giác BDE, ECD, DCB, BEC (định nghĩa đường trung bình).

Đặt BD = CE = 2a

Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:

Suy ra MN = NP = PQ = QM

Tứ giác MNPQ có bốn cạnh bằng nhau nên là hình thoi.

Áp dụng tính chất về đường chéo vào hình thoi MNPQ ta được: MN ⊥ PQ

Đáp án cần chọn là: C

Bài 19: Tứ giác ABCD có AB = CD. Gọi M, N theo thứ tự là trung điểm của BC, AD. Gọi I, K theo thứ tự là trung điểm của AC, BD. Chọn câu đúng nhất.

A. IK vuông góc với MN                   

B. MN là phân giác 

C. Cả A, B đều đúng              

D. Cả A, B đều sai

Lời giải

Từ giả thiết ta có: KM, IM, IN, KN lần lượt là các đường trung bình của các tam giác BCD, CAB, ADC, DBA (định nghĩa đường trung bình).

Đặt BA = CD = 2a.

Áp dụng định lý đường trung bình và giả thiết vào bốn tam giác trên ta được:

Suy ra MK = KN = NI = IM.

Tứ giác KMIN có bốn cạnh bằng nhau nên là hình thoi.

Áp dụng tính chất về đường chéo vào hình thoi KMIN ta được: MN ⊥ KI; MN là đường phân giác 

Đáp án cần chọn là: C

Bài 20: Cho hình thoi ABCD có góc A tù. Biết đường cao kẻ từ đỉnh A đến cạnh CD chia đôi cạnh đó. Tính các góc của hình thoi.

Lời giải

Gọi H là chân đường cao kẻ từ A đến canh CD. Từ giả thiết ta có: AH ⊥ DC, CH = HD suy ra AH là đường trung trực của đoạn CD nên AC = CD. (1)

Do ABCD là hình thoi nên AD = CD (2)

Từ (1) và (2) suy ra AD =CD = AC nên tam giác ACD là tam giác đều, do đó 

Vì góc A và góc D là hai góc trong cùng phía của AB // CD nên chúng bù nhau hay  = 180⁰ – 60⁰ = 120⁰.

Áp dụng tính chất về góc vào hình thoi ta được: 

Đáp án cần chọn là: D

Bài 21: Cho tứ giác ABCD có 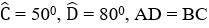. Gọi E, F lần lượt là trung điểm của các cạnh AB và CD. Tính số đo góc EFC.

A. 75⁰             

B. 95⁰             

C. 105⁰           

D. 120⁰

Lời giải

Gọi G, H lần lượt là trung điểm của AC, BD.

Vì E, G lần lượt là trung điểm của AB, AC nên EG là đường trung bình của tam giác ABC. Suy ra EG = ½BC, EG // BC.

Chứng minh tương tự ta cũng có:

Mà AD = BC (gt), nên EG = GF = FH = HE

Đáp án cần chọn là: C

Bài 22: Cho tam giác ABC đều, H là trực tâm, đường cao AD. M là điểm bất kì trên cạnh BC. Gọi E, F lần lượt là hình chiếu của M trên AB, AC, gọi I là trung điểm của đoạn thẳng AM. ID cắt EF tại K.

Chọn câu sai.

A. M, H, K thẳng hang                      

B. ΔIED đều

C. Tứ giác EIFD là hình thoi 

D. ID > IF

Lời giải

Tam giác EAM vuông tại E, EI là đường trung tuyến nên: EI = IM = IA = 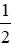AM.

Từ EI = IA suy ra tam giác IAE cân tại I, từ đó có: 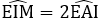 (góc ngoài của tam giác).

Chứng minh tương tự với tam giác vuông ADM ta có: 

Do đó:

Tam giác IED cân (vì EI = DI) có:  = 60⁰ nên là tam giác đều, từ đó EI = ED = ID.

Tương tự tam giác IDF đều suy ra: ID = DF = IF.

Do đó EI = ED = DF = IF. Suy ra tứ giác EIFD là hình thoi.

Suy ra K là trung điểm chung của EF và ID.

Gọi N là trung điểm của AH.

Tam giác ABC đều có H là trực tâm của tam giác ABC nên H cũng là trọng tâm tam giác.

Do đó AN = NH = HD.

Ta có: MH // IN (vì IN là đường trung bình của tam giác AMH) và KH // IN (vì KH là đường trung bình của tam giác DIN).

Từ H ta chỉ vẽ được một đường thẳng song song với IN (tiên đề Ơ – clit) nên M, H, K thẳng hang.

Vậy D sai vì ID = IF.

Đáp án cần chọn là: D

Câu 23: Tứ giác ABCD là hinh thoi có cạnh bằng a thì ta có thể vẽ được:

A.Vô số hình như thế

B.Duy nhất một hình như thế 

C.Không vẽ được hình nào như thế 

D.Hai hình như thế và chúng đối xứng nhau 

Câu 24: Trong hình thoi ABCD, đường cao xuất phát từ đỉnh A chia đôi cạnh BC.Số đo góc kề với mỗi cạnh hình thoi là:

A.30,150

B.40,140

C.50,130

D.60,120

Câu 25: Chu vi của hình thoi ABCD bằng 16cm, đường cao AH bằng 2cm.Số đo góc tù là:

A.110

B.120

C.150

D.Một đáp số khác 

Câu 26: Chọn cách phát biểu đúng:

A.Hình thoi có hai đường chéo vuông góc với nhau và bằng nhau 

B.Tứ giác có hai đường chéo vuông góc với nhau là hình thoi 

C.Hình bình hành có đường chéo là phân giác của các góc đối là hình thoi 

D.Tứ giác có các cạnh đối bằng nhau là hình thoi 

Câu 27: Chọn câu trả lời đúng.

Cho tứ giác MNPQ. Gọi E,F,G,H lần lượt là trung điểm của MN,NP,PQ,QM. Tứ giác EFGH là hình thoi nếu có:

A.MN=PQ

B.MP=NQ

C.MN//PQ

D.MN ⊥ NQMN⊥NQ

Câu 28: Chọn câu trả lời sai

A.Hình bình hành có hai cạnh kề bằng nhau là hình thoi

B.Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi 

C.Hình bình hành có hai đừog chéo vuông góc với nhau là hình thoi 

D.Tứ giác có bốn góc bằng nhau là hình thoi

Câu 29: Câu nào sau đây sai?

A.Trung điểm của cac cạnh hình chữ nhật là các đỉnh của hình thoi 

B.Trung điểm của các cạnh hình thang là các đỉnh của hình thoi 

C.Trung điểm của các cạnh hình thoi là các đỉnh của một hình chữ nhật 

D.Trung điểm của các cạnh hình thoi là cái đỉnh của hình thang cân 

Bài giảng Toán 8 Bài 11: Hình thoi