Tailieumoi.vn xin giới thiệu Giải bài tập Toán 8 Bài 6: Đối xứng trục hay, chi tiết giúp học sinh dễ dàng làm bài tập Đối xứng trục lớp 8.

Giải bài tập Toán lớp 8 Bài 6: Đối xứng trục

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 84 Toán 8 Tập 1: Cho đường thẳng d và một điểm A không thuộc d. Hãy vẽ điểm A’ sao cho d là đường trung trực của đoạn thẳng AA’.

Lời giải

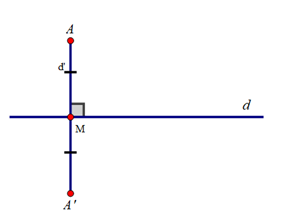
- Vẽ đường thẳng d’ qua A vuông góc với đường thẳng d tại M.

- Trên đường thẳng d’ lấy điểm A’ sao cho MA’ = MA.

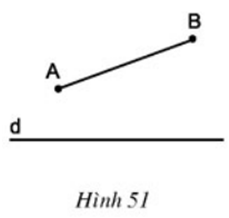
Câu hỏi 2 trang 84 Toán 8 Tập 1: Cho đường thẳng d và đoạn thẳng AB (h.51).

- Vẽ điểm A’ đối xứng với A qua d.

- Vẽ điểm B’ đối xứng với B qua d. 

- Lấy điểm C thuộc đoạn thẳng AB, vẽ điểm C’ đối xứng với C qua d.

- Dùng thước để kiểm nghiệm rằng điểm C’ thuộc đoạn thẳng A’B’.

Lời giải

Khi lấy đối xứng ta được hình vẽ sau:

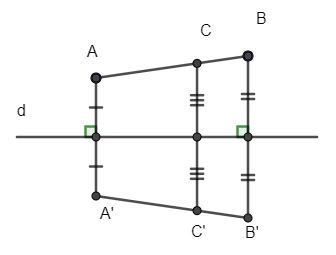
Dùng thước để kiểm tra ba điểm A’, B’ và C’ ta thấy ba điểm này cùng nằm trên một đường thẳng nên ba didemr A’, B’, C’ thẳng hàng.

Câu hỏi 3 trang 86 Toán 8 Tập 1: Cho tam giác ABC cân tại A, đường cao AH (h.55). Tìm hình đối xứng với mỗi cạnh của tam giác ABC qua AH.

Lời giải

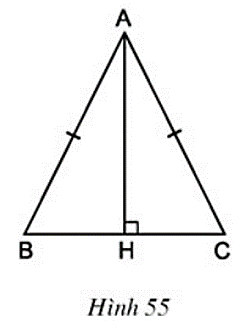
Xét tam giác ABC cân tại A, có AH là đường cao nên AH cũng là đường trung trực của đoạn thẳng BC.

Khi đó, ta có:

Điểm A đối xứng với A qua AH

Điểm C đối xứng với điểm B qua AH

Điểm B đối xứng với điểm C qua AH

Do đó AB đối xứng với AC qua AH, BC đối xứng với CB qua AH.

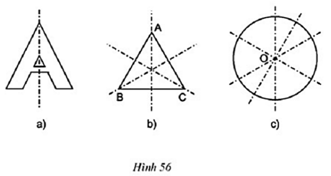
Câu hỏi 4 trang 86 Toán 8 Tập 1: Mỗi hình sau có bao nhiêu trục đối xứng?

a) Chữ cái in hoa A (h.56a)

b) Tam giác đều ABC (h.56b)

c) Đường tròn tâm O

Lời giải

a) Hình 56a) có 1 trục đối xứng

b) Hình 56b) có 3 trục đối xứng

c) Hình 56c) có vô số trục đối xứng

Bài tập (trang 87, 88)

Bài 35 trang 87 Toán 8 Tập 1: Vẽ hình đối xứng với các hình đã cho qua trục d (h.58).

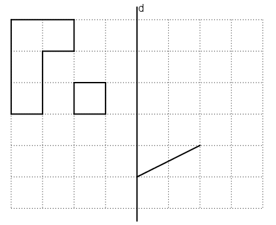
Lời giải:

Vẽ hình:

Bài 36 trang 87 Toán 8 Tập 1: Cho góc xOy có số đo 50^o, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.

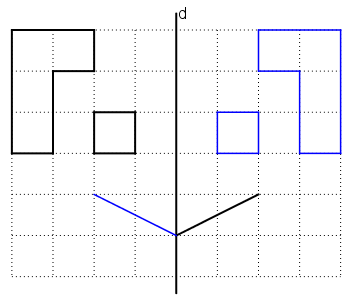
a) So sánh các độ dài OB và OC

b) Tính số đo góc BOC

Lời giải:

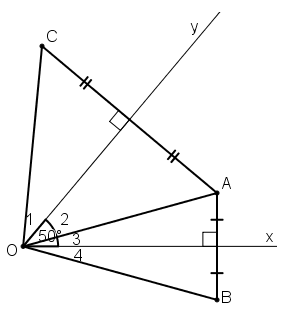
a) + B đối xứng với A qua Ox

⇒ Ox là đường trung trực của AB

⇒ OA = OB (1)

+ C đối xứng với A qua Oy

⇒ Oy là đường trung trực của AC

⇒ OA = OC (2)

Từ (1) và (2) suy ra OB = OC (= OA)

b) Xét ΔOAC có OA = OC

$\Rightarrow \Delta OAC$ cân tại O

Ta có: Oy là đường trung trực của AC

⇒ Oy đồng thời là đường phân giác $\widehat{AOC}$

$\Rightarrow \widehat{O_1}=\widehat{O_2}$ (3)

Xét ΔOAB có OA = OB

$\Rightarrow \Delta OAB$ cân tại O

Ta có Ox là đường trung trực của AB

⇒ Ox đồng thời là đường phân giác

$\Rightarrow \widehat{O_3}=\widehat{O_4}$ (4)

Từ (3) và (4) suy ra $\widehat{O_3}+\widehat{O_2}=\widehat{O_4}+\widehat{O_1}$

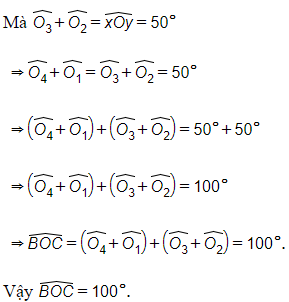
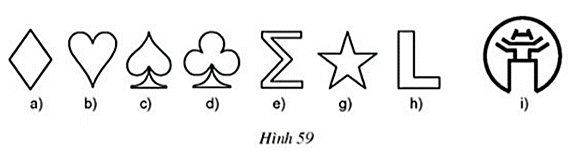
Bài 37 trang 87 Toán 8 Tập 1: Tìm các hình có trục đối xứng trên hình 59.

Lời giải:

+ Hình a có hai trục đối xứng:

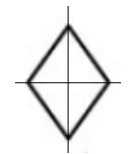
+ Hình b có một trục đối xứng

+ Hình c có một trục đối xứng

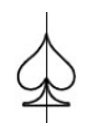
+ Hình d có một trục đối xứng

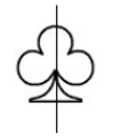
+ Hình e có một trục đối xứng

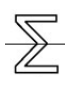
+ Hình g có năm trục đối xứng

+ Hình h không có trục đối xứng

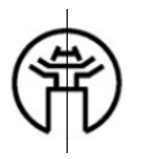
+ Hình i có một trục đối xứng

Bài 38 trang 88 Toán 8 Tập 1: Thực hành. Cắt một tấm bìa hình tam giác cân, một tấm bìa hình thang cân. Hãy cho biết đường nào là trục đối xứng của mỗi hình, sau đó gấp mỗi tấm bìa để kiểm tra lại điều đó.

Lời giải:

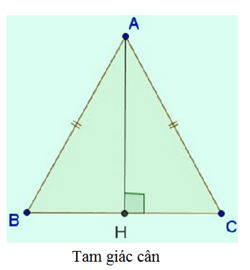
– ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).

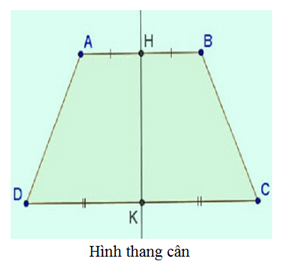
– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.

Bài 39 trang 88 Toán 8 Tập 1: a) Cho hai điểm A, B thuộc cùng một mặt phẳng có bờ là đường thẳng d (h.60). Gọi C là điểm đối xứng với A qua d. Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC. Gọi E là điểm bất kì của đường thẳng d (E khác D).

Chứng minh rằng: AD + DB < AE + EB.

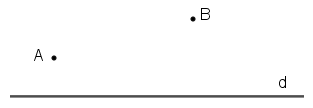
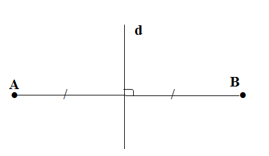
b) Bạn Tú đang ở vị trí A, cần đến bờ sông d lấy nước rồi đi đến vị trí B (h.60). Con đường ngắn nhất mà bạn Tú nên đi là con đường nào?

Lời giải:

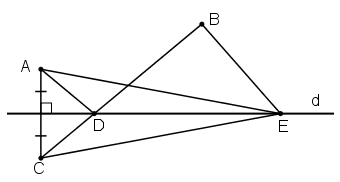
a) + A và C đối xứng qua d

⇒ d là trung trực của AC

⇒ AD = CD

⇒ AD + DB = CD + DB = CB (1)

+ $E\in d\Rightarrow AE=CE$

⇒ AE + EB = CE + EB (2)

+ CB < CE + EB (3)

Từ (1), (2), (3) ⇒ AD + DB < AE + EB

b) Vì với mọi $E\in d$ thì AE + EB > AD + DB

Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.

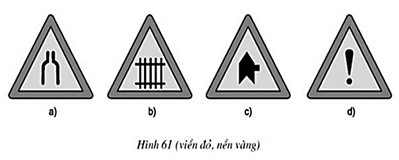
Bài 40 trang 88 Toán 8 Tập 1: Trong các biển báo giao thông sau đây, biển nào có trục đối xứng?

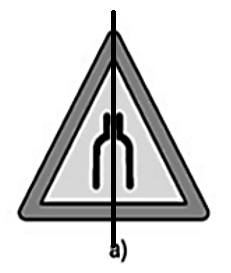
a) Biển nguy hiểm: đường hẹp hai bên (h.61a)

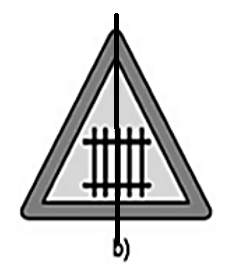
b) Biển nguy hiểm: đường giao thông với đường sắt có rào chắn (h.61b)

c) Biển nguy hiểm: đường ưu tiên gặp đường không ưu tiên bên phải (h.61c)

d) Biển nguy hiểm khác (d.61d)

Lời giải:

- Các biển báo ở hình a, b, d có trục đối xứng.

- Biển báo c không có trục đối xứng.

Bài 41 trang 88 Toán 8 Tập 1: Các câu sau đúng hay sai?

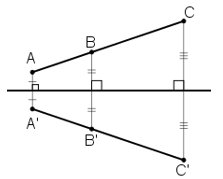
a) Nếu ba điểm thẳng hàng thì ba điểm đối xứng với chúng qua một trục cũng đường thẳng hàng.

b) Hai tam giác đối xứng với nhau qua một trục thì có chu vi bằng nhau.

c) Một đường tròn có vô số trục đối xứng.

d) Một đoạn thẳng chỉ có một trục đối xứng.

Lời giải:

a) Đúng

b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.

c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.

d) Sai.

Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.

Bài 42 trang 89 Toán 8 Tập 1: Đố.

a) Hãy tập cắt chữ D (h.62a) bằng cách gấp đôi tờ giấy. Kể tên một vài chữ cái khác (kiểu chữ in hoa) có trục đối xứng.

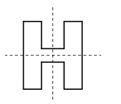
b) Vì sao ta có thể gấp tờ giấy làm tư để cắt chữ H (h.62b)?

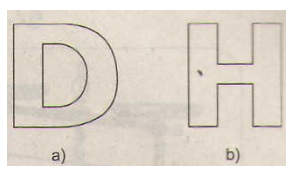
Hình 62

Lời giải:

a) Cắt được chữ D:

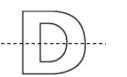
Gấp đôi chữ D theo đường thẳng là trục đối xứng của chữ D như trên hình vẽ.

Một số chữ cái in hoa có trục đối xứng:

- Chỉ có một trục đối xứng dọc: A, M, T, U, V, Y

- Chỉ có một trục đối xứng ngang: B, C, D, E, K

- Có hai trục đối xứng dọc và ngang: H, I, O , X

b) Có thể gấp tờ giấy làm tư để cắt chữ H vì chữ H có hai trục đối xứng vuông góc.