Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn chọn lọc, có đáp án. Tài liệu có 21 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Dấu hiệu nhận biết tiếp tuyến của đường tròn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.

Giới thiệu về tài liệu:

- Số trang: 21 trang

- Số câu hỏi trắc nghiệm: 30 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Dấu hiệu nhận biết tiếp tuyến của đường tròn có đáp án – Toán lớp 9:

Dấu hiệu nhận biết tiếp tuyến của đường tròn

Câu 1: Cho (O; R). Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi:

A. d ⊥ OA tại A và A ∈ (O)                        

B. d ⊥ OA

C. A ∈ (O)                                                 

D. d // OA

Lời giải:

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Đáp án cần chọn là: A

Câu 2: “Nếu một đường thẳng đi qua một điểm của đường tròn và… thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là:

A. song song với bán kính đi qua điểm đó

B. vuông góc với bán kính đi qua điểm đó

C. song song với bán kính đường tròn

D. vuông góc với bán kính bất kì

Lời giải:

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn

Đáp án cần chọn là: B

Câu 3: Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó:

A. Khoảng cách từ O đến đường thẳng d nhỏ hơn 5cm

B. Khoảng cách từ O đến đường thẳng d lớn hơn 5cm

C. Khoảng cách từ O đến đường thẳng d bằng 5cm

D. Khoảng cách từ O đến đường thẳng d bằng 6cm

Lời giải:

Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bắn kính của đường tròn đó

Đáp án cần chọn là: C

Câu 4: Cho (O; 4cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 4cm), khi đó:

A. Khoảng cách từ O đến đường thẳng d nhỏ hơn 4cm

B. Khoảng cách từ O đến đường thẳng d bằng 4cm

C. Khoảng cách từ O đến đường thẳng d lớn hơn 4cm

D. Khoảng cách từ O đến đường thẳng d bằng 5cm

Lời giải:

Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bắn kính của đường tròn đó

Đáp án cần chọn là: B

Câu 5: Cho tam giác ABC có AC = 3cm, AB = 4cm; BC = 5cm. Vẽ đường tròn (M; NM). Khẳng định nào sau đây là đúng?

A. Đường thẳng BC cắt đường tròn (C; CA) tại một điểm

B. AB là cát tuyến của đường tròn (C; CA)

C. AB là tiếp tuyến của (C; CA)

D. BC là tiếp tuyến của (C; CA)

Lời giải:

+) Xét tam giác ABC có:

BC² = 5² = 25; AB² + AC² = 4² + 3² = 25 ⇒ BC² = AB² + AC²

⇒ ∆ABC vuông tại A (định lý Pytago đảo)

⇒ AB ⊥ AC mà A ∈ (C;CA) nên AB là tiếp tuyến của (C; CA)

Đáp án cần chọn là: C

Câu 6: Cho tam giác MNP có MN = 5cm; NP = 12cm; MP = 13cm. Vẽ đường tròn (M; NM). Khẳng định nào sau đây là đúng?

A. NP là tiếp tuyến của (M; MN)       

B. MP là tiếp tuyến của (M;MN)

C. ∆MNP vuông tại M                     

D. ∆MNP vuông tại P

Lời giải:

+) Xét tam giác MNP có MP² = 13² = 169; NM² + NP² = 5² + 12² = 169

⇒ MP² = NM² + NP²

⇒ ∆MNP vuông tại N (định lý Pytago đảo)

⇒ MN ⊥ NP mà N ∈ (M; MN) nên NP là tiếp tuyến của (M; MN)

Đáp án cần chọn là: A

Câu 7: Cho tam giác ABC cân tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI?

A. HK        

B. IB          

C. IC          

D. AC

Lời giải:

Gọi O là trung điểm AI. Xét tam giác vuông AIK có:

Ta đi chứng minh OK ⊥ KH tại K.

Xét tam giác OKA cân tại O có 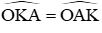 (1)

Vì tam giác ABC cân tại A có đường cao AH nên H là trung điểm của BC. Xét tam giác vuông BKC có 

Từ (1); (2); (3) suy ra góc HKB = góc AKO mà:

Từ (*) và (**) thì HK là tiếp tuyến của đường tròn đường kính AI

Đáp án cần chọn là: A

Câu 8: Cho hình chữ nhật ABCD, H là hình chiếu của A trên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM?

A. BN        

B. MN        

C. AB         

D. CD

Lời giải:

Lấy E là trung điểm của AH. Do M là trung điểm của BH (gt) nên EM là đường trung bình của 

Hình chữ nhật ABCD có CD // AB và CD = AB mà N là trung điểm của DC, suy ra DN // AB và 

Từ (1) và (2) ta có AM // DN và AM = DN

Suy ra tứ giác AMND là hình bình hành, do đó DI // MN

Do EM // AB mà AB ⊥ AD (tính chất hình chữ nhật)

AH ⊥ DM (dt) nên E là trực tâm của ΔADM

Suy ra DE ⊥ AM, mà DE // MN (cmt) ⇒ MN ⊥ AM tại M

Vì vậy MN là tiếp tuyến của đường tròn (A; AM)

Đáp án cần chọn là: B

Câu 9: Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau:

A. DE là cát tuyến của đường tròn đường kính BH

B. DE là tiếp tuyến của đường tròn đường kính BH

C. Tứ giác AEHD là hình chữ nhật

D. DE ⊥ DI (với I là trung điểm BH)

Lời giải:

Gọi I, J lần lượt là trung điểm của BH và CH

Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay >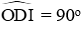

Vì D, E lần lượt thuộc đường tròn đường kính BH và HC nên ta có 

Suy ra tứ giác ADHE là hình chữ nhật

Gọi O là giao điểm của AH và DE, khi đó ta có OD = OH = OE = OA

Ta có ID ⊥ DE, D ∈ (I) nên DE là tiếp tuyến của đường tròn đường kính BH

Từ chứng minh trên, suy ra các phương án B, C, D đúng

Đáp án cần chọn là: A

Câu 11: Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho 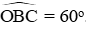. Trên tia OB lấy điểm M sao cho BM = 2cm

Lời giải:

Tam giác OBC cân tại O có 

Nên tam giác OCB là tam giác đều suy ra BC = OB = OC = 2

Xét tam giác OCM có BC = OB = BM = 2 = 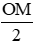 nên ΔOCM vuông tại C

⇒ OC ⊥ CM ⇒ MC là tiếp tuyến của (O; 2cm)

Đáp án cần chọn là: A

Vận dụng

Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho 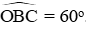. Trên tia OB lấy điểm M sao cho BM = 2cm . Tính độ dài MC

Lời giải:

Tam giác OBC cân tại O có 

Nên tam giác OCB là tam giác đều suy ra BC = OB = OC = 2

Xét tam giác OCM có BC = OB = BM = 2 = 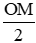  nên ∆OCM vuông tại C

Áp dụng định lý Pytago cho tam giác vuông OCM, ta có M² = OC² + MC²

⇒ MC² = OM² – OC² = 4² – 2² = 12 ⇒ MC = 2√3 cm

Đáp án cần chọn là: C

Câu 12: Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?

A. Hình bình hành

B. Hình thoi

C. Hình thang

D. Hình chữ nhật

Lời giải:

Dễ có AMON là hình bình hành (ON // AM; OM // AN)

Ta chứng minh OM = ON

Đáp án cần chọn là: B

Vận dụng:  Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Điểm A phải cách O một khoảng là bao nhiêu để cho MN là tiếp tuyến của (O)?

Lời giải:

Dễ có AMON là hình bình hành (ON // AM; OM // AN)

Ta chứng minh OM = ON

Vậy OA ⊥ MN mà độ dài OA bằng 2 lần khoảng cách từ O đến MN

Do đó MN là tiếp tuyến của đường tròn (O; R)

⇔ Khoảng cách từ O đến MN bằng R ⇔ OA = 2R

Đáp án cần chọn là: A

Câu 13: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. Chọn khẳng định đúng:

A. BC là cát tuyến của (O)                 

B. BC là tiếp tuyến của (O)

C. BC ⊥ AB                                    

D. BC // AB

Lời giải:

Ta có: OC ⊥ AB ⇒ OC đi qua trung điểm của AB

⇒ OC là đường cao đồng thời là đường trung tuyến của  ∆ABC  ⇒ ∆ABC cân tại C

Đáp án cần chọn là: B

Vận dụng: Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. Cho bán kính của đường tròn bằng 15cm; AB = 24cm. Tính OC

A. OC = 35cm                                  

B. OC = 20cm

C. OC = 25cm                                  

D. OC = 15cm

Lời giải:

Đáp án cần chọn là: C

Câu 14: Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm P. Chọn khẳng định đúng?

Lời giải:

Gọi I là giao điểm của MN và OP

Ta có OP ⊥ MN tại I ⇒ I là trung điểm của MN

⇒ PI là đường cao đồng thời là đường trung tuyến của  MNP

Đáp án cần chọn là: C

Vận dụng: Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm P. Cho bán kính của đường tròn bằng 10cm; MN = 12cm. Tính OP

A. OP = 12,5cm                                

B. OP = 17,5cm

C. OP = 25cm                                   

D. OP = 15cm

Lời giải:

Gọi I là giao điểm của MN và OP

Ta có OP ⊥ MN tại I ⇒ I là trung điểm của MN

Xét tam giác vuông MPO, theo hệ thức lượng trong tam giác vuông ta có:

Vậy OP = 12,5cm

Đáp án cần chọn là: A

Câu 15: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Xác định tâm F của đường tròn đi qua bốn điểm A, D, H, E.

A. F ≡ B                                          

B. F là trung điểm đoạn AD

C. F là trung điểm đoạn AH              

D. F là trung điểm đoạn AE

Lời giải:

Gọi F là trung điểm của AH

Xét hai tam giác vuông AEH và ADH ta có FA = FH = FE = FD = 

Nên bốn đỉnh A, D, H, E cùng thuộc đường tròn tâm F bán kính 

Đáp án cần chọn là: C

Vận dụng: Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm BC. Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến?

A. ME; MD

B. ME        

C. MD        

D. EC

Lời giải:

AH cắt BC tại K ⇒ AK ⊥ BC vì H là trực tâm tam giác ABC

Ta chứng minh ME ⊥ EF tại E

∆FAE cân tại F (vì FA = FE) nên:

∆MEC cân tại M (vì ME = MC = MB = 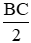) nên 

Từ đó ME là tiếp tuyến của 

Tương tự ta cũng có MD là tiếp tuyến của 

Đáp án cần chọn là: A

Câu 16: Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác góc ABC. BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn đáp án đúng nhất: AHGE là hình gì?

A. Hình bình hành

B. Hình thoi

C. Hình vuông

D. Hình chữ nhật

Lời giải:

Vì D thuộc đường tròn đường kính AB nên BD ⊥ AD ⇒ BD là đường cao của  ΔABG, mà BD là đường phân giác của ABG (gt) nên BD vừa là đường cao vừa là đường phân giác của ΔABG

Do đó ABG cân tại B suy ra BD là trung trực của AG (1)

Vì H đối xứng với E qua D (dt) nên D là trung điểm của HE (2)

Từ (1) và (2) suy ra D là trung điểm của HE và AG

Do đó tứ giác AHGE là hình bình hành (dấu hiệu nhận biết hình bình hành).

Mà HE ⊥ AG nên ΔHGE là hình thoi (dấu hiệu nhận biết hình thoi).

Đáp án cần chọn là: B

Vận dụng: Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác góc ABC. BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn câu đúng:

A. AH là tiếp tuyến của đường tròn đường kính AB

B. HG là tiếp tuyến của đường tròn đường kính AB

C. 

D. Cả A và C đều đúng

Lời giải:

Vì D thuộc đường tròn đường kính AB nên BD ⊥ AD ⇒ BD là đường cao của ΔABG, mà BD là đường phân giác của ABG (gt) nên BD vừa là đường cao vừa là đường phân giác của ΔABG

Do đó ΔABG cân tại B suy ra BD là trung trực của AG (1)

Vì H đối xứng với E qua D (dt) nên D là trung điểm của HE (2)

Từ (1) và (2) suy ra D là trung điểm của HE và AG

Do đó tứ giác AHGE là hình bình hành (dấu hiệu nhận biết hình bình hành).

Mà HE ⊥ AG nên HGE là hình thoi (dấu hiệu nhận biết hình thoi).

Vì tứ giác AHGE là hình thoi nên AH // GE (3) và HE ⊥ AG (tính chất) nên 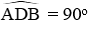 (do đó C đúng)

Xét ΔABG có BD và AC là đường cao, mà BD cắt AC tại E

Suy ra E là trực tâm của ΔABG, do đó GE ⊥ AB (4)

Từ (3) và (4) suy ra AH ⊥ AB

Do đó AH là tiếp tuyến của đường tròn đường kính AB

Đáp án cần chọn là: D

Câu 17: Cho hình vẽ dưới đây. Biết 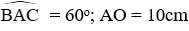. Chọn đáp án đúng.

Độ dài bán kính OB là:

Lời giải:

Từ hình vẽ ta có AB, AC là tiếp tuyến của (O) tại B, C suy ra OC ⊥ AC tại C

Đáp án cần chọn là: B

Thông hiểu: Cho hình vẽ dưới đây. Biết 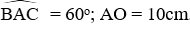. Chọn đáp án đúng.

Độ dài tiếp tuyến AB là:

Lời giải:

Từ hình vẽ ta có AB, AC là tiếp tuyến của (O) tại B, C suy ra OC ⊥ AC tại C

Đáp án cần chọn là: C

Câu 18: Cho hình vẽ dưới đây. Biết AB và AC là hai tiếp tuyến của (O), 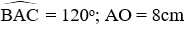. Chọn đáp án đúng.

Độ dài bán kính OB là:

Lời giải:

Vì AB, AC là tiếp tuyến của (O) tại B, C suy ra OB ⊥ AB tại B và OC ⊥ AC tại C

Đáp án cần chọn là: A

Thông hiểu: Cho hình vẽ dưới đây. Biết AB và AC là hai tiếp tuyến của (O), 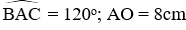. Chọn đáp án đúng.

Độ dài đoạn AB là:

Lời giải:

Vì AB, AC là tiếp tuyến của (O) tại B, C suy ra OB ⊥ AB tại B và OC ⊥ AC tại C

Đáp án cần chọn là: D

Câu 19: Cho nửa đường tròn (O; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho CD = 3R. Chọn câu đúng.

A. AD là tiếp tuyến của đường tròn   

B. 

C. AD cắt đường tròn (O; R) tại hai điểm phân biệt

D. Cả A, B đều đúng

Lời giải:

Vì AB là đường kính của (O; R) nên AB = 2R

Vì D thuộc tia đối của tia CB nên BD = CD + BC = 3R + R = 4R

B. 

Đáp án cần chọn là: D

Câu 20: Cho 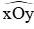, trên Ox lấy P, trên Oy lấy Q sao cho chu vi ΔPOQ bằng 2a không đổi. Chọn câu đúng.

A. PQ luôn tiếp xúc với một đường tròn cố định

B. PQ không tiếp xúc với một đường tròn cố định nào

C. PQ = a

D. PQ = OP

Lời giải:

Gọi I là giao điểm các tia phân giác của 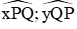 và A, B, C lần lượt là hình chiếu của I lên Ox, PQ và Oy

Vì I thuộc phân giác của góc xPQ nên IA = IB

nên ΔPAI = ΔPBI (cạnh huyền – cạnh góc vuông)

Suy ra PA = PB

Lí luận tương tự, ta có QB = QC.

OA + OC = OP + PA + OQ + QC = OP + PB + OQ + QB = OP + PQ + QO = 2a (do chu vi ΔOPQ bằng 2a)

Vì IA = IB và IB = IC (cmt) nên IA = IC

nên ΔOAI = ΔOCI (cạnh huyền – cạnh góc vuông)  

Vì a không đổi và A, C thuộc tia Ox, Oy cố định nên A và C cố định

Do A và C lần lượt là hình chiếu của I lên Ox, Oy nên hai đường thẳng AI và CI cố định hay I cố định

Do I và A cố định nên độ dài đoạn thẳng AI không đổi

Do IA = IB (cmt) nên IB là bán kính của đường tròn (I; IA) mà IB ⊥ PQ tại B nên PQ tiếp xúc với đường tròn (I; IA) cố định

Đáp án cần chọn là: A

Bài giảng Toán 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến cảu đường tròn