Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 5: Công thức nghiệm thu gọn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 5: Công thức nghiệm thu gọn
Bài 27 trang 55 SBT Toán 9 tập 2: Xác định a, b’, c trong mỗi phương trình, rồi giải phương trình bằng công thức nghiệm thu gọn:
a)
b)
c)
d)
Phương pháp giải:
Phương trình và ,
+ Nếu thì phương trình có hai nghiệm phân biệt:
;
+ Nếu thì phương trình có nghiệm kép .
+ Nếu thì phương trình vô nghiệm.
Lời giải:
a)
Có hệ số
Phương trình có hai nghiệm phân biệt là:
b)
Có hệ số
Phương trình có hai nghiệm phân biệt là:
c)
Có hệ số
Phương trình vô nghiệm.
d)
Có hệ số
Phương trình có nghiệm kép:
Bài 28 trang 55 SBT Toán 9 tập 2: Với những giá trị nào của
thì giá trị của hai biểu thức bằng nhau:
a) và
b) và
c) và
d) và
e) và ?
Phương pháp giải:
Phương trình và ,
+ Nếu thì phương trình có hai nghiệm phân biệt:
;
+ Nếu thì phương trình có nghiệm kép .
+ Nếu thì phương trình vô nghiệm.
Lời giải:
a)
Phương trình có hai nghiệm phân biệt:
Vậy với hoặc thì hai biểu thức đã cho bằng nhau.
b)
Phương trình có hai nghiệm phân biệt:
Vậy hoặc thì hai biểu thức đó bằng nhau.
c)
Phương trình có hai nghiệm phân biệt:
Vậy hoặc thì hai biểu thức bằng nhau.
d)
Phương trình có hai nghiệm phân biệt:
Vậy hoặc thì hai biểu thức bằng nhau.
e)
Phương trình có hai nghiệm phân biệt:
Vậy và thì hai biểu thức bằng nhau.
Bài 29 trang 55 SBT Toán 9 tập 2: Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách
từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức:
Hỏi khoảng cách x bằng bao nhiêu:
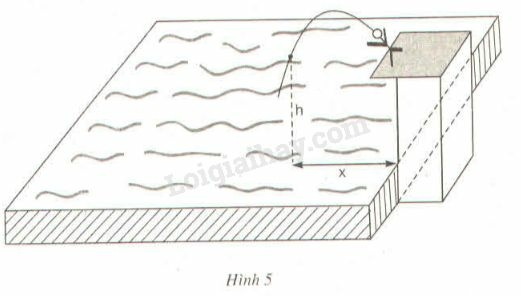
a) Khi vận động viên ở độ cao ?
b) Khi vận động viên chạm mặt nước?
Phương pháp giải:
Thay vào phương trình , từ đó ta tìm .
Khi chạm mặt nước ta có , thay vào phương trình từ đó ta tìm .
* Phương trình và ,
+ Nếu thì phương trình có hai nghiệm phân biệt:
;
+ Nếu thì phương trình có nghiệm kép .
+ Nếu thì phương trình vô nghiệm.
Lời giải:
a)
Khi ta có:
Vậy hoặc .
b)
Khi vận động viên chạm mặt nước ta có .
Vì khoảng cách không âm nên .
Bài 30 trang 56 SBT Toán 9 tập 2: Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai):
a)
b)
c)
d)
Phương pháp giải:
Phương trình và ,
+ Nếu thì phương trình có nghiệm kép .
Lời giải:
a)
Phương trình có nghiệm kép:
b)
Phương trình có hai nghiệm phân biệt:
c)
Phương trình có hai nghiệm phân biệt:
d)
Phương trình có hai nghiệm phân biệt:
Bài 31 trang 56 SBT Toán 9 tập 2: Với giá trị nào của
thì giá trị của hai hàm số bằng nhau:
a) và
b) và ?
Phương pháp giải:
Phương trình và ,
+ Nếu thì phương trình có hai nghiệm phân biệt:
;
+ Nếu thì phương trình có nghiệm kép .
+ Nếu thì phương trình vô nghiệm.
Lời giải:
a)
Phương trình có nghiệm kép:
Vậy thì hàm số và hàm số có giá trị bằng nhau.
b)
Phương trình có hai nghiệm phân biệt:
Vậy hoặc thì giá trị của hai hàm số và bằng nhau.
Bài 32 trang 56 SBT Toán 9 tập 2: Với giá trị nào của
thì:
a) Phương trình có một nghiệm
b) Phương trình có một nghiệm ?
Phương pháp giải:
Thay vào phương trình từ đó giải phương trình bậc hai ẩn .
Lời giải:
a)
Vì là nghiệm của phương trình (1)
Nên thay vào phương trình , ta được:
Vậy hoặc thì phương trình (1) có nghiệm .
b)
Vì là nghiệm của phương trình (2)
Nên thay vào phương trình , ta được:
Vậy hoặc thì phương trình (2) có nghiệm .
Bài 33 trang 56 SBT Toán 9 tập 2: Với giá trị nào của
thì phương trình có hai nghiệm phân biệt:
a)
b)
Phương pháp giải:
Phương trình có hai nghiệm phân biệt khi và chỉ khi và .
Lời giải:
a)
Phương trình có hai nghiệm phân biệt khi và chỉ khi
Vậy thì phương trình đã cho có hai nghiệm phân biệt.
b)
Phương trình có hai nghiệm phân biệt khi và chỉ khi và
Vậy và thì phương trình đã cho có hai nghiệm phân biệt.
Bài 34 trang 56 SBT Toán 9 tập 2: Với giá trị nào của
thì phương trình có nghiệm kép:
a)
b)
Phương pháp giải:
Phương trình có nghiệm kép khi và chỉ khi và .
Lời giải:
a)
Phương trình có nghiệm kép khi và chỉ khi
Giải phương trình:
Ta có:
Vậy hoặc thì phương trình đã cho có nghiệm kép.
b)
Phương trình có nghiệm kép khi và chỉ khi và
Ta có với mọi
Nên phương trình vô nghiệm.
Vậy không có giá trị nào của để phương trình có nghiệm kép.
Bài tập bổ sung (trang 56 SBT Toán 9)
Bài 5.1 trang 56 SBT Toán 9 tập 2: Giả sử
là hai nghiệm của phương trình bậc hai
có
. Điều nào sau đây là đúng?
A)
B)
C)
D)
Phương pháp giải:
Phương trình và ,
+ Nếu thì phương trình có hai nghiệm phân biệt:
;
+ Nếu thì phương trình có nghiệm kép .
+ Nếu thì phương trình vô nghiệm.
Lời giải:
Giả sử là hai nghiệm của phương trình bậc hai có thì
Chọn B.
Bài 5.2 trang 56 SBT Toán 9 tập 2: Tìm mối liên hệ giữa
để phương trình
có nghiệm.
Phương pháp giải:
Tìm điều kiện để phương trình (1) có nghiệm ta xét hai trường hợp sau:
- TH1: từ đó tìm nghiệm của (1).
- TH2: , phương trình (1) có nghiệm khi và chỉ khi .
Lời giải:
- TH1: và .
Khi đó phương trình đã cho có dạng: (*)
Phương trình (*) có nghiệm khi .
Vậy thì phương trình đã cho có vô số nghiệm.
- TH2:
Phương trình có nghiệm khi và chỉ khi
suy ra và không đồng thời bằng
Vì
Vậy thì phương trình đã cho có nghiệm.
Bài 5.3 trang 56 SBT Toán 9 tập 2: Chứng tỏ rằng phương trình
luôn có nghiệm.
Phương pháp giải:
Phương trình và , luôn có nghiệm khi và chỉ khi .
Đối với bài này ta chứng minh phương trình đã cho có .
Lời giải:
Ta có:
Suy ra:
Vậy phương trình luôn có nghiệm.
