Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 1 Bài 2: Tỷ số lượng giác của góc nhọn. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 2: Tỷ số lượng giác của góc nhọn. Mời các bạn đón xem:
Bài tập Toán 9 Chương 1 Bài 2: Tỉ số lượng giác của góc nhọn
A. Bài tập Tỷ số lượng giác của góc nhọn
I. Bài tập trắc nghiệm
Câu 1: Cho tam giác MNP vuông tại M. Khi đó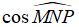 
bằng
Chọn đáp án A
Câu 2: Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.
Cho α là góc nhọn bất kỳ, khi đó sin2α + cos2α = 1
Chọn đáp án B
Câu 3: Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.
Cho α là góc nhọn bất kỳ, khi đó
Chọn đáp án D
Câu 4: Cho α và β là góc nhọn bất kỳ thỏa mãn α + β = 90° . Chọn khẳng định đúng.
A. α + β = 90°
B. tanα = cotβ
C. tanα = cosα
D. tanα = tanβ
Với hai góc α và β mà α + β = 90 °
sinα = cosβ; cosα = sinβ
tanα = cotβ ; cotα = tanβ
Chọn đáp án B
Câu 5: Cho tam giác ABC vuông tại c có BC = 1,2 cm, AC = 0,9 cm . Tính các tỉ số lượng giác sinB; cosB
Chọn đáp án A
Câu 6: Cho tam giác ABC vuông tại A, AB = 30 cm. Biết tan B = 8/15. Tìm khẳng định sai trong các khẳng định sau :
Chọn đáp án A.
Câu 7: Cho tam giác ABC vuông tại A. Tính 
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông ta có:
Chọn đáp án A.
Câu 8: Cho tam giác ABC vuông tại A có đường trung tuyến ứng với cạnh huyền AM = 10 cm; AB = 16 cm . Tính cot B?
Do tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền nên:
Chọn đáp án D.
Áp dụng định lí Pytago vào tam giác ABH vuông tại H ta có:
AH2 + BH2 = AB2
⇔ AH2 = AB2 - BH2 = 132 - 52 = 144
⇔ AH = 12cm
Áp dụng tỉ số lượng giác của nhọn trong tam giác vuông ABH ta có:
Do tam giác BAC là tam giác vuông nên hai góc B và C là 2 góc phụ nhau.
Suy ra:
Chọn đáp án B.
Câu 10: Cho tam giác ABC vuông tại A có AC = 8cm và góc C = 60°. Tính diện tích tam giác ABC .
A. 32 cm2
B. 16√3 cm2
C. 16 cm2
D. 32√3 cm2
Chọn đáp án D.
Câu 11: Cho tam giác ABC vuông tại A có BC = 9cm; AC = 5cm. Tính tỉ số lượng giác tan C (làm tròn đến chữ số thập phân thứ 1)
A. tan C ≈ 0,67
B. tan C ≈ 0,5
C. tan C ≈ 1,4
D. tan C ≈ 1,5
Đáp án cần chọn là: D
Câu 12: Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, BH = 0,5dm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)
A. sin C ≈ 0,35
B. sin C ≈ 0,37
C. sin C ≈ 0,39
D. sin C ≈ 0,38
Đổi 0,5dm = 5cm
Xét tam giác ABC vuông tại A, theo hệ thức lượng trong tam giác vuông ta có:
Đáp án cần chọn là: D
Câu 13: Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có
Mà tam giác ABC vuông tại A nên là hai góc phụ nhau.
Đáp án cần chọn là: B
Câu 14: Cho tam giác ABC vuông tại A, ∠ABC = 60o, cạnh AB = 5cm. Độ dài cạnh AC là:
Đáp án cần chọn là: C
Câu 15: Cho tam giác ABC vuông tại A, đường cao AH có CH = 4cm, BH = 3cm. Tính tỉ số lượng giác cos C (làm tròn đến chữ số thập phân thứ 2)
A. cos C ≈ 0,76
B. cos C ≈ 0,77
C. cos C ≈ 0,75
D. cos C ≈ 0,78
Lời giải:
Xét tam giác ABC vuông tại A có BC = BH + CH = 7cm
Theo hệ thức lượng trong tam giác vuông ta có:
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Biết sinα = 5/13. Tính cosα, tanα và cotα.
Lời giải:
Xét ΔABC vuông tại A.
Câu 2: Biết sinα.cosα = 12/25. Tính sinα, cosα.
Lời giải:
Biết sinα.cosα = 12/25. Để tính sinα,cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα.
Ta có:
III. Bài tập vận dụng
Câu 1: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .
Câu 2: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: 
B. Lý thuyết Tỷ số lượng giác của góc nhọn
1. Khái niệm tỉ số lượng giác của một góc nhọn
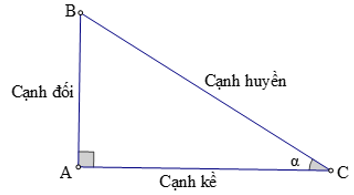
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cos α.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tan α.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cot α.
Ví dụ 1. Cho tam giác ABC có .
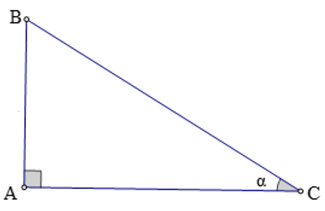
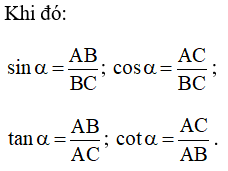
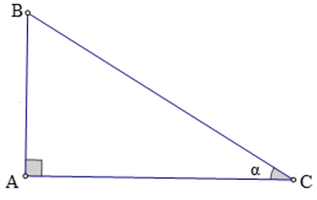
Nhận xét: Nếu α là một góc nhọn thì:
0 < sin α < 1; 0 < cos α < 1; tan α > 0; cot α > 0.
Ví dụ 2. Cho tam giác ABC có
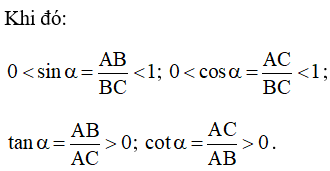
Chú ý: Nếu hai góc nhọn α và β có sin α = sin β (hoặc cos α = cos β, hoặc tan α = tan β, hoặc cot α = cot β) thì α = β vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.
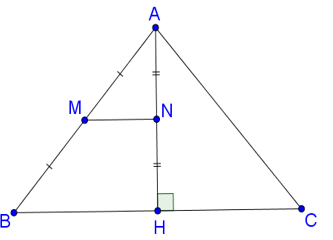
Ví dụ 3. Cho tam giác ABC có AB = AC, đường cao AH. MN là đường trung bình của tam giác ABH. Chứng minh .
Lời giải:
Vì AH là đường cao của ∆ABC nên hay (1)
Mà MN là đường trung bình của ∆AMN nên:
+ AB = 2AM; AH = 2AN.
+ MN // BH (2)
Từ (1) và (2) suy ra (tính chất từ vuông góc đến song song).
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí. Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Ví dụ 4. Cho tam giác ABC vuông tại A có .
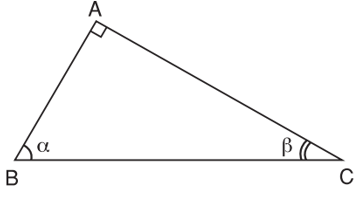
Khi đó, α + β = 90° (trong tam giác vuông hai góc nhọn phụ nhau).
Ta có: sin α = cos β; cos α = sin β; tan α = cot β; cot α = tan β.
Bảng lượng giác của một số góc đặc biệt:
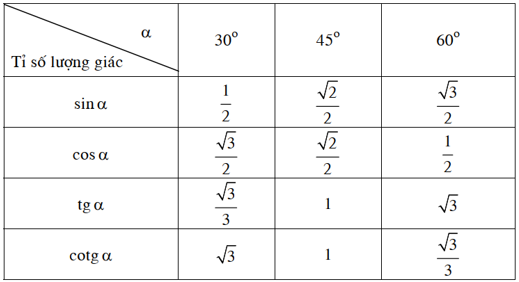
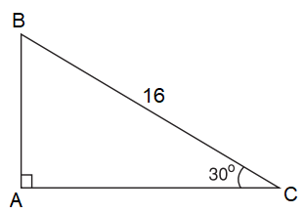
Ví dụ 5. Cho tam giác ABC vuông tại A có BC = 16, . Tính độ dài AB.
Lời giải:
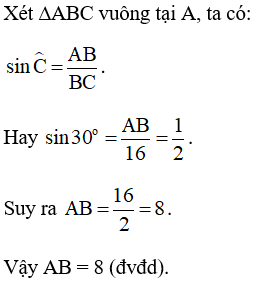
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu " ^ " đi.
Ví dụ 6. Góc A là góc nhọn thì ta viết sin A thay cho .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
