Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9: Ứng dụng thực tế tỉ số lượng giác của góc nhọn chọn lọc, có đáp án. Tài liệu có 18 trang gồm 26 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Ứng dụng thực tế tỉ số lượng giác của góc nhọn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.
Giới thiệu về tài liệu:
- Số trang: 18 trang
- Số câu hỏi trắc nghiệm: 26 câu
- Lời giải & đáp án: có
Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Ứng dụng thực tế tỉ số lượng giác của góc nhọn có đáp án – Toán lớp 9:

Ứng dụng thực tế tỉ số lượng giác của góc nhọn
Câu 1: Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5m. Hãy tính góc 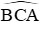
A. 58o45’
B. 59o50’
C. 59o45’
D. 59o4’
Lời giải:
Ta có:
Đáp án cần chọn là: C
Câu 2: Một cột đèn điện AB cao 7m có bóng in trên mặt đất là AC dài 4m. Hãy tính góc 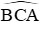
A. 59o45’
B. 62o
C. 61o15’
D. 60o15’
Lời giải:
Đáp án cần chọn là: D
Câu 3: Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
A. 14,3m
B. 15,7m
C. 16,8m
D. 17,2m
Lời giải:
Chiều cao của cây là: h = 1,7 + 20. tan35o ≈ 15,7m
Đáp án cần chọn là: B
Câu 4: Một cây tre cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
A. 6m
B. 5m
C. 4m
D. 3m
Lời giải:
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) ⇔ CB = CD = 9 – x. Vì ∆ACD vuông tại A
Suy ra AC2 + AD2 = CD2
⇔ x2 + 32 = (9 – x)2 ⇔ x = 4 (TM)
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C
Câu 5: Một cây tre cao 8m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3,5m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
A. 3,32m
B. 3,23m
C. 4m
D. 3m
Lời giải:
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x ⇔ CB = CD = 8 – x.
Vậy điểm gãy cách gốc cây 3,23m
Đáp án cần chọn là: B