Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn Toán lớp 9, tài liệu bao gồm 8 trang, tuyển chọn Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Tài liệu Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn gồm các nội dung chính sau:

I. Phương phương giải

- Tóm tắt lý thuyết ngắn gọn.

II. Bài tập

- Gồm 9 bài tập tự luyện có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập sự xác định đường tròn. Tính chất đối xứng của đường tròn.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI TẬP SỰ XÁC ĐỊNH ĐƯỜNG TRÒN.

TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN

I. Phương pháp giải

1. Nhắc lại về đường tròn

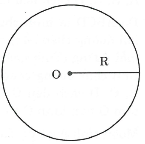
Đường tròn tâm $O$, bán kính $R\left(R>0\right)$ là hình gồm các điểm cách điểm $O$ một khoảng bằng R kí hiệu $\left(O;R\right)$ cũng có thể là $\left(O\right)$ khi không cần chú ý đến bán kính.

- Khi có điểm M nằm trên đường tròn $\left(O\right)$ bán kính R ta viết $OM=R$

- Nếu điểm M nằm bên trong $\left(O;R\right)$ ta viết $OM<R$

- Nếu điểm M nằm bên ngoài $\left(O;R\right)$ ta viết $OM>R$

2. Cách xác định một đường tròn

a) Một điểm O cho trước và một số thực $r>0$ cho trước xác định một đường tròn tâm O bán kính r

b) Một đoạn thẳng AB cho trước xác định một đường tròn đường kính AB

c) Nếu có 3 điểm không thẳng hàng bao giờ cũng xác định được một đường tròn đi qua 3 điểm đó. Đường tròn đi qua 3 điểm $A,B,C$ của $\Delta ABC$ gọi là đường tròn ngoại tiếp $\Delta ABC$. $\Delta ABC$ gọi là tam giác nội tiếp đường tròn.

3. Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.

4. Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào cũng là trục đối xứng của đường tròn.

II. Bài tập   

Bài 1: (1/99/SGK T1)

Cho hình chữ nhật $ABCD$ có $AB=12cm,BC=5cm$. Chứng minh rằng 4 điểm $A,B,C,D$ cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Giải

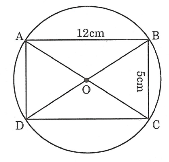
Muốn chứng minh 4 điểm $A,B,C,D$ cùng nằm trên một đường tròn, ta chứng minh $A,B,C,D$ cách đều một điểm O.

Do $ABCD$ là hình chữ nhật (giả thiết) nên $AC=BD$ (Hình chữ nhật có hai đường chéo bằng nhau) mà $AC$ và $BD$ cắt nhau tại trung điểm O của mỗi đường (Tính chất đường chéo của hình bình hành đồng thời cũng là tính chất đường chéo của hình chữ nhật) $\Rightarrow OA=OB=OC=OD\Rightarrow A,B,C,D$ cách đều O. Vậy 4 điểm $A,B,C,D$ cùng nằm trên đường tròn tâm $O$ bán kính OA

Muốn tính được độ dài bán kính đường tròn $\left(O\right)$ đi qua 4 điểm $A,B,C,D$ ta phải tính độ dài của $AC$ là cạnh huyền của $\Delta ABC$ vuông tại B nên:

$A{C}^2=A{B}^2+B{C}^2$ (Định lý Py – ta – go) $={12}^2+5^2=144+25=169\Rightarrow AC=\sqrt{169}=13$

$\Rightarrow OA=OC=\frac{AC}{2}=\frac{13}{2}=6,5$

Vậy bán kính của đường tròn tâm $\left(O\right)$ qua bốn điểm $A,B,C,D$ có độ dài là 6,5 cm.

Bài 2: (2/100/SGK T1)

Hãy nối mỗi ô ở cộ trái với một ô ở cột phải để được một khẳng định đúng.