Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 2 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 2 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn. Mời các bạn đón xem:
Bài tập Toán 9 Chương 2 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
A. Bài tập Sự xác định đường tròn. Tính chất đối xứng của đường tròn
I. Bài tập trắc nghiệm
Câu 1: Số tâm đối xứng của đường tròn là
A. 1
B. 2
C. 3
D. 4
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn
Chọn đáp án A
Câu 2: Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
A. Đường tròn không có trục đối xứng
B. Đường tròn có duy nhất một trục đối xứng là đường kính
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
D. Đường tròn có vô số trục đối xứng là đường kính
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Chọn đáp án D
Câu 3: Tâm của đường tròn ngoại tiếp tam giác là
A. Giao của ba đường phân giác
B. Giao của ba đường trung trực
C. Giao của ba đường cao
D. Giao của ba đường trung tuyến
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó
Chọn đáp án B
Câu 4: Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn
B. Điểm M nằm trên đường tròn
C.Điểm M nằm trong đường tròn
D. Điểm M không thuộc đường tròn
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
Chọn đáp án B
Câu 5: Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a
A. Tâm là giao điểm A và bán kính R = a√2
B. Tâm là giao điểm hai đường chéo và bán kính R = a√2
C. Tâm là giao điểm hai đường chéo và bán kính
D. Tâm là điểm B và bán kính là
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác vuông tại ta có:
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Chọn đáp án C
Câu 6: Cho tam giác ABC vuông tại A. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là?
A. Điểm A
B. Điểm B .
C. Chân đường cao hạ từ A
D. Trung điểm của BC
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Chọn đáp án D.
Câu 7: Cho tứ giác ABCD là hình bình hành và 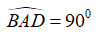
A. Trung điểm AC B . Điểm A
C. Điểm B
D. Điểm D
Vì tứ giác ABCD là hình bình hành và 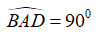
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Chọn đáp án A.
Câu 8: Cho 4 điểm phân biệt A, B, C và D sao cho tam giác ABC vuông tại A và tam giác BCD vuông tại
D. Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Điểm A
B. Điểm B
C. Trung điểm BC
D. Trung điểm AD
Gọi I là trung điểm BC.
Ta có; tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
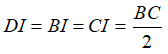
Tam giác ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC nên:
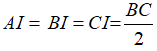
Từ (1) và (2) suy ra:
Do đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.
Chọn đáp án C
Câu 9: Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
A. Điểm A.
B. Giao điểm của AC và BD
C. Không có đường tròn ngoại tiếp tứ giác ABCD.
D. Trung điểm cạnh AB.
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Chọn đáp án B
Câu 10: Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm ........
A. có khoảng cách đến điểm I bằng 4cm
B. Có khoảng cách đến điểm I nhỏ hơn 4 cm.
C. Có khoảng cách đến điểm I lớn hơn 4 cm.
D. có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Chọn đáp án D.
Câu 11: Tâm của đường tròn ngoại tiếp tam giác vuông là:
A. Trung điểm cạnh huyền
B. Trung điểm cạnh góc vuông lớn hơn
C. Giao ba đường cao
D. Giao ba đường trung tuyến
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Đáp án cần chọn là: A
Câu 12: Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông?
A. bằng cạnh nhỏ nhất của tam giác vuông
B. bằng nửa cạnh góc vuông lớn hơn
C. bằng nửa cạnh huyền
D. bằng 4cm
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền
Đáp án cần chọn là: C
Câu 13: Cho tam giác ABC có các đường cao BD, CE. Biết rằng bốn điểm B, E, D, C cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
A. Tâm là trọng tâm tam giác ABC và bán kính 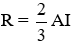
B. Tâm là trunng điểm AB và bán kính
C. Tâm là giao điểm của BD và EC, bán kính
D. Tâm là trung điểm BC và bán kính
Gọi I là trung điểm của BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Đáp án cần chọn là: D
Câu 14: Cho tam giác ABC có các đường cao BD, CE. Chọn khẳng định đúng.
A. Bốn điểm B, E, D, C cùng nằm trên một đường tròn
B. Năm điểm A, B, E, D, C cùng nằm trên một đường tròn
C. Cả A, B, đều sai
D. Cả A, B đều đúng
Gọi I là trung điểm BC.
Xét tam giác BEC vuông tại E có EI = IB = IC = 
Xét tam giác BDC vuông tại D có DI = IB = IC = 
Từ đó ta có ID = IE = IB = IC = 
Ta thấy IA > ID nên điểm A không thuộc đường tròn trên
Đáp án cần chọn là: A
Câu 15: Trên mặt phẳng tọa độ Oxy, xác định vị trí tương đối của điểm A (−1; −1) và đường tròn tâm là gốc tọa độ O, bán kính R = 2
A. Điểm A nằm ngoài đường tròn
B. Điểm A nằm trên đường tròn
C. Điểm A nằm trong đường tròn
D. Không kết luận được
Lời giải:
Ta có 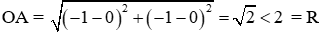
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
Câu 1: Cho tam giác đều ABC có cạnh bằng a. AB, BN, CP là các đường trung tuyến. Chứng minh 4 điểm B, P, N, C cùng thuộc một đường tròn. Tính bán kính đường tròn đó.
Lời giải:
Vì tam giác ABC đều nên các trung tuyến đồng thời cũng là đường cao .
Suy ra AM, BN, CP lần lượt vuông góc với BC, AC, AB.
Từ đó ta có các tam giác BPC, BNC là tam giác vuông với BC là cạnh huyền
Tam giác BPC vuông tại P có đường trung tuyến PM nên PM = BM = MC = 1/2 BC (1)
Tam giác BNC vuông tại N có đường trung tuyến NM nên NM = MB = MC = 1/2 BC (2)
Từ (1) và (2) suy ra: PM = NM = MB = MC = 1/2 BC
Hay: Các điểm B, P, N, C cùng thuộc đường tròn
Đường kính BC = a, tâm đường tròn là trung điểm M của BC
Câu 2: Cho tứ giác ABCD có ∠C + ∠D = 90°. Gọi M, N, P, Q lần lượt là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng thuộc một đường tròn. Tìm tâm đường tròn đó .
Lời giải:
Kéo dài AD, CB cắt nhau tại điểm T thì tam giác TCD vuông tại T.
+ Do MN là đường trung bình của tam giác ABD nên NM // AD
+ MQ là đường trung bình của tam giác ABC nên MQ // BC. Mặt khác AD ⊥ BC ⇒ MN ⊥ MQ.
Chứng minh tương tự ta cũng có: MN ⊥ NP, NP ⊥ PQ. Suy ra MNPQ là hình chữ nhật.
Hay các điểm M, N, P, Q thuộc một đường tròn có tâm là giao điểm O của hai đường chéo NQ, MP
III. Bài tập vận dụng
Câu 1: Chứng minh rằng đường tròn ngoại tiếp tam giác vuông có tâm chính là trung điểm của cạnh huyền
Câu 2: Cho hình chữ nhật ABCD có AB = 10, BC = 8 . Chứng minh rằng A, B, C, D cùng thuộc một đường tròn và tính bán kính của đường tròn đó
B. Lý thuyết Sự xác định đường tròn. Tính chất đối xứng của đường tròn
1. Khái niệm cơ bản
Đường tròn tâm O bán kính R (với R > 0) là hình gồm các điểm cách đều điểm O một khoảng không đổi bằng R.
Đường tròn tâm O bán kính R được kí hiệu là (O;R), hay gọn hơn (O).
Đoạn thẳng nối hai điểm bất kì trên đường tròn gọi là một dây của đường tròn.
Dây đi qua tâm là đường kính của đường tròn (đường kính dài gấp đôi bán kính).
2. Vị trí tương đối của điểm M và đường tròn (O,R)
Cho đường tròn (O;R) và một điểm M. Khi đó
1. M nằm trên (O;R) khi và chỉ khi OM = R
2. M nằm bên trong (O;R) khi và chỉ khi OM < R
3. M nằm bên ngoài (O;R) khi và chỉ khi OM > R
3. Điều kiện để xác định đường tròn
1. Một đường tròn được xác định khi biết tâm và bán kính của nó.
2. Một đường tròn được xác định khi biết một đoạn thẳng là đường kính của đường tròn đó.
3. Qua ba điểm không thẳng hàng cho trước ta vẽ được một và chỉ một đường tròn.
4. Tính chất đối xứng của đường tròn
Tính chất 1. Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
Tính chất 2. Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào cũng là trục đối xứng của đường tròn.