Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Các bài toán khai thác định nghĩa, tính chất và ứng dụng của phép đối xứng trục và đối xứng tâm Toán lớp 11, tài liệu bao gồm 5 trang, tuyển chọn 10 bài toán khai thác định nghĩa, tính chất và ứng dụng của phép đối xứng trục và đối xứng tâm đầy đủ lý thuyết, phương pháp giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Tài liệu Các bài toán khai thác định nghĩa, tính chất và ứng dụng của phép đối xứng trục và đối xứng tâm gồm các nội dung sau:
I. Phương pháp
- Tóm tắt lý thuyết ngắn gọn cần nhớ
II. Ví dụ
- Gồm 10 ví dụ minh họa đa dạng cho Các bài toán khai thác định nghĩa, tính chất và ứng dụng của phép đối xứng trục và đối xứng tâm có lời giải chi tiết
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
DẠNG 3. KHAI THÁC DỊNH NGHĨA, TINH CHẤT VA ỨNG DỤNG CỦA PHÉP ĐỐI XỨNG TRỤC VÀ ĐỐI XỨNG TÂM.
I. Phương pháp :
- Sử dụng định nghĩa hoặc tính chất của phép đối xứng trục, đối xứng tâm.
- Xác định ảnh của một điểm, một hình qua phép đối xứng trục, đối xứng tâm.
- Tìm quỹ tích điểm thông qua phép đối xứng trục, đối xứng tâm.
- Vận dụng đối xứng trục, đối xứng tâm để giải các bài toán hình học khác…
II. VÍ DỤ
Ví dụ 1: Cho đường thẳng a. Qua phép đối xứng trục a, đường thẳng nào biến thành chính nó.
A. Các đường thẳng song song với a.
B. Các đường thẳng vuông góc với a.
C. Các đường thẳng hợp với một góc .
D. Các đường thẳng hợp với một góc .
Đáp án B.
Lời giải:
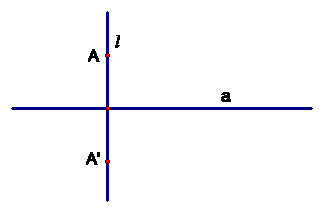
Giả sử là đường thẳng vuông góc với a.
Lấy và và ngược lại vẫn thỏa mãn
Ví dụ 2: Cho hai đường thẳng cắt nhau d và d' . có bao nhiêu phép đối xứng trục biến đường thẳng này thành đường thẳng kia?
A. Không có. B. Một. C. Hai. D. Vô số.
Lời giải:
Đáp án C.
Có 2 phép đối xứng trục với các trục là hai đường phân giác của góc tạo bởi hai đường thẳng cắt nhau d và d'
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
