Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài tập phép dời hình và phép đồng dạng trong mặt phẳng, tài liệu bao gồm 52 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập phép dời hình và phép đồng dạng trong mặt phẳng có lời giải chi tiết

Chủ đề 6. Phép dời hình và phép đồng dạng trong mặt phẳng

Bài 01 : Phép biến hình

Định nghĩa

Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất \({M^\prime }\) của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.

Nếu ký hiệu phép biến hình là F thì ta viết \(F(M) = {M^\prime }\) hay \({M^\prime } = F(M)\) và gọi điểm \({M^\prime }\) là ảnh của điểm M qua phép biến hình F.

Nếu \(\mathcal{H}\) là một hình nào đó trong mặt phẳng thì ta kí hiệu \({\mathcal{H}^\prime } = F(\mathcal{H})\) là tập các điểm \({M^\prime } = F(M)\), với mọi điểm M thuộc \(\mathcal{H}\). Khi đó ta nói F biến hình \(\mathcal{H}\) thành hình \({\mathcal{H}^\prime }\), hay hình \({\mathcal{H}^\prime }\) là ảnh của hình \((\mathcal{H})\) qua phép biến hình F.

Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

Bài 02 Phép tịnh tiến

1. Định nghĩa

Trong mặt phẳng cho vectơ \(\vec v\). Phép biến hình biến mỗi điểm M thành điểm \({M^\prime }\) sao cho \(\overrightarrow {M{M^\prime }}  = \vec v\) được gọi là phép tịnh tiến theo vectơ \(\vec v\).

Phép tịnh tiến theo vectơ \(\vec v\) thường được lí hiệu là \({T_{\vec v}},\vec v\) được gọi là vectơ tịnh tiến.

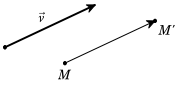
Như vậy

\({T_{\vec v}}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \vec v.\)

Phép tịnh tiến theo vecto – không chính là phép đồng nhất.

2. Tính chất

Tính chất 1. Nếu \({T_ - }(M) = {M^\prime },{T_v}(N) = {N^\prime }\)thì \(\overrightarrow {{M^\prime }{N^\prime }}  = \overrightarrow {MN} \) và tù đó suy ra \({M^\prime }{N^\prime } = MN\).

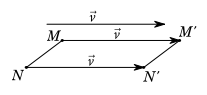
Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.

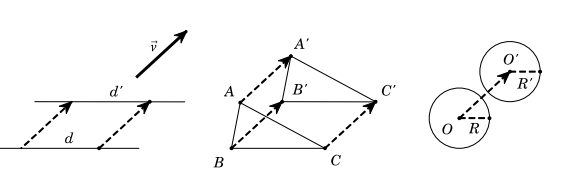
3. Biểu thức tốc độ

Trong mặt phẳng tọa độ Oxy cho vectơ \(\vec v = (a;b)\). Với mỗi điểm M(x;y) ta có \({M^\prime }\left( {{x^\prime };{y^\prime }} \right)\) là ảnh của M qua phép tịnh tiến theo \(\vec v\). Khi đó

\(\overrightarrow {M{M^\prime }}  = \vec v \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } - x = a}\\{{y^\prime } - y = b}\end{array} \to \left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array}.} \right.} \right.\)

Biểu thức trên được gọi là biểu thức tọa độ của phép tịnh tiến \({T_{\vec v}}\).

Câu hỏi và bài tập trắc nghiệm 11

Câu hỏi trắc nghiệm

Câu 1. Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải. Có đúng một phép tịnh tiến. Tịnh tiến theo vectơ-không. Chọn B.

Câu 2. Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải. Có đúng một phép tịnh tiến. Tịnh tiến theo vectơ-không. Chọn B.

Câu 3. Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải. Khi tịnh tiến đường thẳng theo vectơ \(\vec v\) có phương cùng phương với đường thẳng thì đường thẳng biến thành chính nó.

Mà có vô số vectơ \(\vec v\) có phương cùng phương với đường thẳng.

Vậy có vô số phép tịnh tiến biến một đường thẳng thành chính nó. Chọn D.

Câu 4. Cho hai đường thẳng d và \({d^\prime }\) song song với nhau. Có bao nhiêu phép tịnh tiến biến d thành \({d^\prime }\) ?

A. 1 .

B. 2 .

C. 3 .

D. Vô số.

Lời giải. Trên \(d,{d^\prime }\) lần lượt lấy \(A,{A^\prime }\) bất kì.

Khi đó, \({d^\prime }\) là ảnh của d qua phép tịnh tiến vectơ \(\overrightarrow {A{A^\prime }} \).

Vậy có vô số phép tịnh tiến biến d thành \({d^\prime }\) thỏa mãn d song song \({d^\prime }\). Chọn D.

Câu 5. Cho bốn đường thẳng \(a,b,{a^\prime },{b^\prime }\) trong đó \(a//{a^\prime },b//{b^\prime }\) và a cắt b. Có bao nhiêu phép tịnh tiến biến a thành \({a^\prime }\) và \(b\) thành \({b^\prime }\) ?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải.

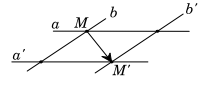
Giả sử a cắt b tại \(M;{a^\prime }\) cắt \({b^\prime }\) tại \({M^\prime }\).

Khi đó vectơ \(\overrightarrow {M{M^\prime }} \) là vectơ tịnh tiến thỏa mãn yêu cầu bài toán. Chọn B.

Câu 6. Cho đường thẳng a cắt hai đường thằng song song b và \({b^\prime }\). Có bao nhiêu phép tịnh tiến biến đường thẳng a thành chính nó và biến đường thẳng b thành đường thẳng \({b^\prime }\) ?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải.

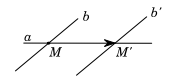
Giả sử a cắt b tại \(M\); cắt \({b^\prime }\) tại \({M^\prime }\).

Khi đó vectơ \(\overrightarrow {M{M^\prime }} \) là một vectơ tịnh tiến thỏa mãn yêu cầu bài toán. Chọn B.

Câu 7. Cho hình bình hành ABCD. Có bao nhiêu phép tịnh tiến biến đường thẳng A B thành đường thẳng CD và biến đường thẳng AD thành đường thẳng BC ?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải.

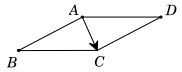
Có một phép tịnh tiến duy nhất theo vectơ tịnh tiến \(\overrightarrow {AC} \). Chọn B.

Câu 8. Có bao nhiêu phép tịnh tiến biến đồ thị của hàm số y = sinx thành chính nó?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Lời giải.

Có vô số phép tịnh tiến theo vectơ \(k2\pi \) với \(k \in \mathbb{Z}\). Chọn D.

Câu 9. Giả sử qua phép tịnh tiến theo vectơ \(\vec v \ne \vec 0\), đường thẳng d biến thành đường thẳng \({d^\prime }\). Mệnh đề nào sau đây sai?

A. d trùng \({d^\prime }\) khi \(\vec v\) là vectơ chỉ phương của d.

B. d song song \({d^\prime }\) khi \(\vec v\) là vectơ chî phương của d.

C. d song song \({d^\prime }\) khi \(\vec v\) không phải là vectơ chỉ phương của d.

D. d không bao giờ cắt \({d^\prime }\).

Lời giải. Chọn B.

Câu 10. Cho hai đường thẳng song song d và \({d^\prime }\). Tất cả những phép tịnh tiến biến d thành \({d^\prime }\) là:

A. Các phép tịnh tiến theo vectơ \(\vec v\), với mọi vectơ \(\vec v \ne 0\) có giá không song song với giá vetơ chỉ phương của d.

B. Các phép tịnh tiến theo vectơ \(\vec v\), với mọi vectơ \(\vec v \ne 0\) vuông góc với vec-tơ chỉ phương của d.

C. Các phép tịnh tiến theo \(\overrightarrow {A{A^\prime }} \), trong đó hai điểm A và \({A^\prime }\) tùy ý lần lượt nằm trên d và \({d^\prime }\).

D. Các phép tịnh tiến theo vectơ \(\vec v\), với mọi vectơ \(\vec v \ne 0\) tùy ý.

Lời giải. Chọn C.

A sai, ví dụ lấy A và \({A^\prime }\) tùy ý lần lượt nằm trên d và \({d^\prime }\). Khi đó, phép tịnh tiến theo vectơ \(2\overrightarrow {A{A^\prime }} \) sẽ không biến d thành \({d^\prime }\).

B thiếu những vectơ có phương không vuông góc và không cùng phương với phương của d.

D sai, vì \(\vec v\) có phương cùng phương với phương của \(d\) thì \(d \equiv {d^\prime }\).

Câu 11. Mệnh đề nào sau đây là sai?

A. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.

C. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.

D. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.

Lời giải. D sai, vì phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho. Chọn D.

Câu 12. Cho phép tịnh tiến theo \(\vec v = \vec 0\), phép tịnh tiến \({T_{\vec 0}}\) biến hai điểm M và N thành hai điểm \({M^\prime }\) và \({N^\prime }\). Mệnh đề nào sau đây là đúng?

A. Điểm M trùng với điểm N.

B. \(\overrightarrow {MN}  = \vec 0\).

C. \(\overrightarrow {M{M^\prime }}  = \overrightarrow {N{N^\prime }}  = \vec 0\).

D. \(\overrightarrow {{M^\prime }{N^\prime }}  = \vec 0\).

Lời giải. Ta có \[\left\{ {\begin{array}{*{20}{l}}{{T_{\vec 0}}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \vec 0}\\{{T_{\vec 0}}(N) = {N^\prime } \Leftrightarrow \overrightarrow {N{N^\prime }}  = \vec 0}\end{array}} \right.\]

\[ \to \overrightarrow {M{M^\prime }}  = \overrightarrow {N{N^\prime }}  = \vec 0\]. Chọn C.

Câu 13. Cho phép tịnh tiến vectơ \(\vec v\) biến A thành \({A^\prime }\) và M thành \({M^\prime }\). Mệnh đề nào sau đây là đúng?

A. \(\overrightarrow {AM}  = \overrightarrow {{A^\prime }{M^\prime }} \). \(\quad \)

B. \(\overrightarrow {AM}  = 2\overrightarrow {{A^\prime }{M^\prime }} \).

C. \(\overrightarrow {AM}  =  - \overrightarrow {{A^\prime }{M^\prime }} \)

D. \(3\overrightarrow {AM}  = 2\overrightarrow {{A^\prime }{M^\prime }} \).

Lời giải.

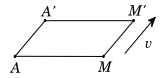
Ta có \(\overrightarrow {A{A^\prime }}  = \vec v\) và \(\overrightarrow {M{M^\prime }}  = \vec v\).

- Nếu \(A \equiv M \Rightarrow {A^\prime } \equiv {M^\prime } \to \overrightarrow {AM}  = \overrightarrow {{A^\prime }{M^\prime }}  = \vec 0\).

- \(A \ne M \to A{A^\prime }{M^\prime }M\) là hình bình hành \( \to \overrightarrow {AM}  = \overrightarrow {{A^\prime }{M^\prime }} \).

Vậy ta luôn có \(\overrightarrow {AM}  = \overrightarrow {{A^\prime }{M^\prime }} \). Chọn A.

Câu 14. Cho hình bình hành A B C D, M là một điểm thay đổi trên cạnh AB. Phép tịnh tiến theo vectơ \(\overrightarrow {BC} \) biến điểm M thành \({M^\prime }\). Mệnh nào sau đây đúng?

A. Điểm \({M^\prime }\) trùng với điểm M.

B. Điểm \({M^\prime }\) nằm trên cạnh BC.

C. Điểm \({M^\prime }\) là trung điểm cạnh CD.

D. Điểm \({M^\prime }\) nằm trên cạnh DC.

Lời giải.

Ta có \({T_{\overrightarrow {BC} }}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \overrightarrow {BC}  \to {M^\prime } \in CD\). Chọn D.

Câu 15. Một phép tịnh tiến biến điểm A thành điểm B và biến điểm C thành điểm D. Khẳng định nào sau đây là sai?

A. A B C D là hình bình hành.

B. \(\overrightarrow {AC}  = \overrightarrow {BD} \).

C. Trung điểm của hai đoạn thẳng AD và BC trùng nhau.

D. \(\overrightarrow {AB}  = \overrightarrow {CD} \).

Lời giải. Chọn A. Phát biểu lại cho đúng là " A B D C là hình bình hành" .

Câu 16. Cho hai đoạn thẳng AB và \({A^\prime }{B^\prime }\). Điều kiện cần và đủ để có thể tịnh tiến biến A thành \({A^\prime }\) và biến B thành \({B^\prime }\) là

A. \(AB = {A^\prime }{B^\prime }\).

B. \(AB//{A^\prime }{B^\prime }\).

C. Tứ giác \(AB{B^\prime }{A^\prime }\) là hình bình hành.

D. \(\overrightarrow {AB}  = \overrightarrow {{A^\prime }{B^\prime }} \).

Lời giải. giả sử có phép tịnh tiến \({T_{\vec v}}\) biến A thành \({A^\prime }\) và biến B thành \({B^\prime }\).

Khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}{{T_{\vec v}}(A) = {A^\prime } \Leftrightarrow \overrightarrow {A{A^\prime }}  = \vec v}\\{{T_{\vec v}}(B) = {B^\prime } \Leftrightarrow \overrightarrow {B{B^\prime }}  = \vec v}\end{array} \Rightarrow \overrightarrow {A{A^\prime }}  = \overrightarrow {B{B^\prime }} } \right.\)

\( \to \overrightarrow {AB}  + \overrightarrow {B{A^\prime }}  = \overrightarrow {B{A^\prime }}  + \overrightarrow {{A^\prime }{B^\prime }}  \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {{A^\prime }{B^\prime }} \). Chọn D.

Chú ý : Rất dễ nhầm lẫn chọn C. Vì đề bài không nói \(A \ne {A^\prime }\) nên chưa chắc \(AB{B^\prime }{A^\prime }\) là hình bình hành. Hoặc 4 điểm \(A,B,{A^\prime },{B^\prime }\) thẳng hàng thì khi đó C sai.

Câu 17. Cho phép tịnh tiến \({T_{\vec u}}\) biến điểm M thành \({M_1}\) và phép tịnh tiến \({T_{\vec v}}\) biến \({M_1}\) thành \({M_2}\). Mệnh đề nào sau đây đúng?

A. Phép tịnh tiến \({T_{\vec u + \vec v}}\) biến \({M_1}\) thành \({M_2}\).

B. Một phép đối xứng trục biến \(M\) thành \({M_2}\).

C. Không khẳng định được có hay không một phép dời hình biến M thành \({M_2}\).

D. Phép tịnh tiến \({T_{\vec u + \vec v}}\) biến M thành \({M_2}\).

Lời giải. Ta có \(\left\{ {\begin{array}{*{20}{l}}{{T_{\vec u}}(M) = {M_1} \Leftrightarrow \overrightarrow {M{M_1}}  = \vec u}\\{{T_{\vec v}}\left( {{M_1}} \right) = {M_2} \Leftrightarrow \overrightarrow {{M_1}{M_2}}  = \vec v}\end{array}} \right.\)

\( \to \vec u + \vec v = \overrightarrow {M{M_1}}  + \overrightarrow {{M_1}{M_2}}  = \overrightarrow {M{M_2}} \)

Đẳng thức \(\overrightarrow {M{M_2}}  = \vec u + \vec v\) chứng tỏ phép tịnh tiến \({T_{\vec u + \vec v}}\) biến M thành \({M_2}\). Chọn D.

Câu 18. Cho hai điểm P, Q cố định. Phép tịnh tiến T biến điểm M bất kỳ thành \({M^\prime }\) sao cho \(\overrightarrow {M{M^\prime }}  = 2\overrightarrow {PQ} \). Khẳng định nào sau đây là đúng?

A. T là phép tịnh tiến theo vectơ \(\overrightarrow {PQ} \).

B. T là phép tịnh tiến theo vectơ \(\overrightarrow {MM} \) '.

C. T là phép tịnh tiến theo vectơ \(2\overrightarrow {PQ} \).

D. T là phép tịnh tiến theo vectơ \(\frac{1}{2}\overrightarrow {PQ} \).

Lời giải. Đẳng thức \(\overrightarrow {M{M^\prime }}  = 2\overrightarrow {PQ} \) chứng tỏ phép tịnh tiến \({T_{2\overrightarrow {PQ} }}\) biến M thành \({M^\prime }\).

Chọn C.

Câu 19. Trong mặt phẳng tọa độ Oxy cho véctơ \(\vec v = (a;b)\). Giả sử phép tịnh tiến theo \(\vec v\) biến điểm M(x;y) thành \({M^\prime }\left( {{x^\prime };{y^\prime }} \right)\). Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ \(\vec v\) là:

A. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x = {x^\prime } + a}\\{y = {y^\prime } + b}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } - b = x - a}\\{{y^\prime } - a = y - b}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } + b = x + a}\\{{y^\prime } + a = y + b}\end{array}} \right.\).

Lời giải. Ta có \(\overrightarrow {M{M^\prime }}  = \left( {{x^\prime } - x;{y^\prime } - y} \right)\).

Theo giả thiết

\[\begin{array}{l}{T_{\vec v}}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \vec v\\ \to \left\{ {\begin{array}{*{20}{l}}{{x^\prime } - x = a}\\{{y^\prime } - y = b}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array}} \right.} \right.\end{array}\]

Chọn A.