Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển tập 171 bài toán xác suất đủ mức độ, tài liệu bao gồm 63 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển tập 171 bài toán xác suất đủ mức độ có đáp án và lời giải chi tiết

Tuyển Tập Xác Suất Đủ Mức Độ.

Câu 1. Lớp 11B có 20 học sinh gồm 12 nữ và 8 nam. Cần chọn ra 2 học sinh của lớp đi lao động. Tính xác suất để chọn được 2 học sinh trong đó có cả nam và nữ.

A. \[\frac{{14}}{{95}}\].

B. \[\frac{{48}}{{95}}\].

C. \[\frac{{33}}{{95}}\].

D. \[\frac{{47}}{{95}}\].

Hướng dẫn giải

Số cách chọn 2 trong số 20 học sinh là \[C_{20}^2\]= 190 ⇒ n(Ω) = 190.

Gọi A là biến cố: “2 học sinh được chọn có cả nam và nữ ”.

Số kết quả thuận lời cho A là \[C_8^1.C_{12}^1\]= 96 ⇒ n(A) = 96.

Vậy, \[P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{48}}{{95}}\].

Chọn đáp án B

Câu 2. Gieo một con súc sắc cân đối và đồng chất. Giả sử súc sắc xuất hiện mặt b chấm. Tính xác suất để phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt.

A. \[\frac{3}{5}\]

B. \[\frac{5}{6}\]

C. \[\frac{1}{3}\]

D. \[\frac{2}{3}\]

Hướng dẫn giải

Phương trình x² + bx + 2 = 0 có hai nghiệm phân biệt khi

 ∆ = b² − 8 > 0 ⇔ \[\left[ {\begin{array}{*{20}{c}}{b > 2\sqrt 2 }\\{b <  - 2\sqrt 2 }\end{array}} \right.\]

Vì số chấm xuất hiện ở mỗi mặt của con súc sắc là một số tự nhiên từ 1 đến 6 nên b ∈ {3, 4, 5, 6}. Vậy xác suất cần tìm là P = \[\frac{4}{6} = \frac{2}{3}\].

Chọn đáp án D

Câu 3. Chọn ngẫu nhiên 2 học sinh từ một tổ có 9 học sinh. Biết rằng xác suất chọn được 2 học sinh nữ bằng \[\frac{5}{{18}}\], hỏi tổ có bao nhiêu học sinh nữ?

A 5.

B 3.

C 4.

D 6.

Hướng dẫn giải Gọi số học sinh nữ là n (2 ≤ n < 9, n ∈ N).

Chọn bất kỳ 2 học sinh ta có \[C_9^2\] = 36 cách.

Để chọn 2 học sinh được 2 học sinh nữ có \[C_n^2 = \frac{{n(n + 1)}}{2}\]cách.

Xác suất để chọn được 2 học sinh nữ là \[\frac{{n(n + 1)}}{{72}} = \frac{5}{{18}} \Leftrightarrow n = 4\].

Chọn đáp án C

Câu 4. Gọi X là tập hợp tất cả các số tự nhiên có 8 chữ số lập từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một số trong tập hợp X. Xác suất để số chọn ra có đúng ba chữ số 1, các chữ số còn lại đôi một khác nhau và hai chữ số chẵn không đứng cạnh nhau bằng

A.\[\frac{{25}}{{2916}}\].

B. \[\frac{{105}}{{4096}}\].

 C. \[\frac{{35}}{{8748}}\].

D. \[\frac{{25}}{{17496}}\].

Hướng dẫn giải Số phần tử của tập X là 6⁸ . Để tạo ra số có đúng ba chữ số 1, các chữ số còn lại đôi một khác nhau và hai chữ số chẵn không đứng cạnh nhau ta làm như sau:

Sắp xếp 5 chữ số lẻ trong đó có 3 chữ số 1 ta có \[\frac{{5!}}{{3!}}\]= 20 cách xếp.

Với mỗi cách sắp xếp như thế sẽ tạo ra 6 chỗ để đưa vào các chữ số chẵn. Chẳng hạn như 11135

Để tạo ra số thỏa yêu cầu bài toán ta xếp các chữ số 2; 4; 6 vào 6 chỗ trên sao cho mỗi ô trống chỉ chứa đúng 1 chữ số. Như vậy có \[A_6^3\] = 120

Vậy xác suất đề bài cần tìm là P = \[\frac{{20.120}}{{{6^8}}} = \frac{{25}}{{17496}}\].

Chọn đáp án D

Câu 5. Có hai thùng đựng rượu Bầu Đá, một loại rượu nổi tiếng của thị xã An Nhơn, tỉnh Bình Định. Thùng thứ nhất đựng 10 chai gồm 6 chai rượu loại một và 4 chai rượu loại hai. Thùng thứ hai đựng 8 chai gồm 5 chai rượu loại một và 3 chai rượu loại hai. Lấy ngẫu nhiên mỗi thùng một chai, tính xác suất để lấy được ít nhất 1 chai rượu loại một. Biết rằng các chai rượu giống nhau về hình thức (rượu loại một và loại hai chỉ khác nhau về nồng độ cồn) và khả năng được chọn là như nhau.

A. \[\frac{7}{9}\].

B. \[\frac{1}{2}\].

C. \[\frac{3}{{20}}\].

D. \[\frac{{17}}{{20}}\].

Hướng dẫn giải

Số phần tử không gian mẫu là n(Ω) = 10 · 8 = 80.

Gọi A là biến cố “Lấy được ít nhất 1 chai rượu loại một”.

Số trường hợp thuận lợi cho A là n(A) = 6 · 5 + 6 · 3 + 5 · 4 = 68.

Vậy xác suất cần tính là P(A) = \[\frac{{n(A)}}{{n(\Omega )}} = \frac{{17}}{{20}}\].

Chọn đáp án D

Câu 6. Người dân Bình Định truyền nhau câu ca dao:

“Muốn ăn bánh ít lá gai

Lấy chồng Bình Định sợ dài đường đi.”

Muốn ăn bánh ít lá gai thì bạn phải tìm về với xứ Tuy Phước - Bình Định. Nơi đây nổi tiếng trứ danh với món bánh nghe cái tên khá lạ lẫm “Bánh ít lá gai” và hương vị làm say đắm lòng người. Trong một lô sản phẩm trưng bày bánh ít lá gai ở hội chợ ẩm thực huyện Tuy Phước gồm 40 chiếc bánh, 25 chiếc bánh có nhiều hạt mè và 15 chiếc bánh có ít hạt mè, một du khách chọn ngẫu nhiên 5 chiếc bánh, tính xác suất để du khách đó chọn được ít nhất 2 chiếc bánh có nhiều hạt mè (các chiếc bánh có khả năng được chọn là như nhau).

A. \[\frac{{1990}}{{2109}}\].

B. \[\frac{{1800}}{{2109}}\].

C. \[\frac{{1184}}{{2109}}\].

D. \[\frac{{1892}}{{2109}}\].

Hướng dẫn giải

Gọi A là biến cố có ít nhất 2 chiếc bánh có nhiều mè.

Suy ra \[\overline A \] là biến cố có 1 chiếc bánh hoặc không có chiếc bánh nào có nhiều mè.

Số cách chọn 4 chiếc ít mè và 1 chiếc bánh nhiều mè là \[C_{15}^4.C_{25}^1\].

Số cách chọn cả 5 chiếc ít mè là \[C_{15}^5\].

\[P(A) = 1 - P(\overline A ) = 1 - \frac{{C_{15}^4.C_{25}^1 + C_{15}^5}}{{C_{40}^5}} = \frac{{1990}}{{2109}}\].

Chọn đáp án A

Câu 7. Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nghiên cùng một lúc ba tấm thẻ. Tính xác suất sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?

A. \[\frac{{17}}{{25}}\].

B. \[\frac{{27}}{{52}}\].

C. \[\frac{{253}}{{325}}\].

D. \[\frac{{1771}}{{2600}}\].

Hướng dẫn giải

Để bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị thì phải rút được ba thẻ sao cho trong đó không có hai thẻ nào là hai số tự nhiên liên tiếp.

Số phần tử của không gian mẫu (số cách rút ba thẻ bất kì) là: \[C_{26}^3\].

Số cách rút ba thẻ có đúng 2 số tự nhiên liên tiếp:

Chọn các bộ hai số tự nhiên liên tiếp: (1; 2),(2, 3), · · ·(25; 26).

Nếu chọn hai thẻ là (1; 2) và (25; 26) thì có 2 cách, thẻ còn lại không được là 3 hoặc 24. Vậy ở trường hợp này có tất cả 2(26 − 3) = 46 cách chọn.

Nếu chọn hai thẻ là (2; 3),(3, 4), · · ·(24; 25) thì có 23 cách, thẻ còn lại chỉ có 26 − 4 = 22 cách. Vậy ở trường hợp này có tất cả 23 · 22 = 506 cách chọn.

Số cách rút ba thẻ trong đó ba ba thẻ đều là ba số tự nhiên liên tiếp là 24 cách.

Suy ra có \[C_{26}^3\]− 46 − 506 − 24 = 2024 cách rút được ba thẻ sao cho trong đó không có hai thẻ nào là hai số tự nhiên liên tiếp.

Vậy xác suất cần tìm là \[P = \frac{{2024}}{{C_{26}^3}} = \frac{{253}}{{325}}.\]

Chọn đáp án C

Câu 8. Một hộp chứa 12 quả cầu gồm 7 quả cầu màu xanh và 5 quả cầu màu đỏ. Chọn ngẫu nhiên đồng thời 3 quả cầu từ hộp đó. Xác suất để 3 quả cầu chọn ra cùng màu trắng bằng

A. \[\frac{7}{{44}}\].

B. \[\frac{{35}}{{22}}\].

C. \[\frac{9}{{44}}\].

D. \[\frac{1}{{22}}\].

Hướng dẫn giải

Số phần tử của không gian mẫu: n_Ω = \[C_{12}^3\]= 220.

Gọi A là biến cố: “Chọn được ba quả cầu cùng màu”.

Ta có n(A) = \[C_7^3 + C_5^3\]= 45.

P(A) = \[\frac{{45}}{{220}} = \frac{9}{{44}}\].

Chọn đáp án C

Câu 9. Gọi A là tập hợp tất cả các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc A. Tính xác suất để số tự nhiên được chọn chia hết cho 25. A. \[\frac{{17}}{{81}}\].

B. \[\frac{{43}}{{324}}\].

C. \[\frac{1}{{27}}\].

D. \[\frac{{11}}{{324}}\].

Hướng dẫn giải

Số các số tự nhiên có 8 chữ số đôi một khác nhau là \[9.A_9^7\].

Trong các số trên, số tự nhiên chia hết cho 25 khi hai chữ số cuối chia hết cho 25. Vậy hai chữ số cuối có dạng 25 hoặc 50 hoặc 75.

2 chữ số cuối là 25, có \[7.A_5^5\]số.

2 chữ số cuối là 50, có \[A_8^6\] số.

2 chữ số cuối là 75, có \[7.A_7^5\] số.

Vậy xác suất cần tìm là \[\frac{{7.A_5^5 + A_8^6 + 7.A_7^5}}{{9.A_9^7}} = \frac{{11}}{{324}}.\]

Chọn đáp án D

Câu 10. Gieo một con súc sắc cân đối và đồng chất. Tính xác suất để xuất hiện mặt có số chấm chia hết cho 3.

A. 1.

B. 3.

C. \[\frac{2}{3}\].

D. \[\frac{1}{3}\].

Hướng dẫn giải

Ta có n (Ω) = 6.

Gọi A: “Mặt có số chấm chia hết cho 3” ⇒ A = {3, 6} ⇒ n(A) = 2.

Xác suất cần tìm P(A) = \[\frac{{n(A)}}{{n(\Omega )}} = \frac{1}{4}\].

Chọn đáp án D

Câu 11. Thầy giáo có 10 câu hỏi trắc nghiệm, trong đó có 6 câu đại số và 4 câu hình học. Thầy gọi bạn Nam lên trả bài bằng cách chọn lấy ngẫu nhiên 3 câu hỏi trong 10 câu hỏi trên đê trả lời. Hỏi xác suất bạn Nam chọn ít nhất có một câu hình học là bằng bao nhiêu?

A. \[\frac{1}{6}\].

B. \[\frac{1}{{30}}\].

C. \[\frac{{29}}{{30}}\].

D. \[\frac{5}{6}\].

Hướng dẫn giải

Không gian mẫu: n(Ω) = \[C_{10}^3\].

Gọi A là biến cố có ít nhất một câu hình. n(A) = \[C_4^1.C_6^2 + C_4^2.C_6^1 + C_4^3\].

P(A) = \[\frac{{n(A)}}{{n(\Omega )}} = \frac{5}{6}\].

Chọn đáp án D

Câu 12. Cho đa giác đều 18 cạnh. Nối tất cả các đỉnh với nhau. Chọn 2 tam giác trong số các tam giác vuông tạo thành từ 3 đỉnh trong 18 đỉnh. Xác suất để chọn được hai tam giác vuông có cùng chu vi là

A. \[\frac{{35}}{{286}}\].

B. \[\frac{{70}}{{143}}\].

C. \[\frac{{35}}{{143}}\].

D. \[\frac{{10}}{{33}}\].

Hướng dẫn giải

Xét hai tam giác vuông ABC và A’BC có chung cạnh huyền và có chu vi bằng nhau. Đặt \[\varphi  = \widehat {ABC};\varphi ' = \widehat {A'BC},{0^0} < \varphi ,\varphi ' < {90^0}\].

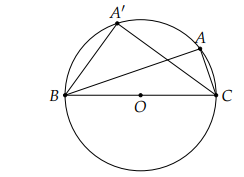
Chu vi hai tam giác bằng nhau khi BC(sin ϕ + cos ϕ) = BC(sin ϕ’ + cos ϕ’)

⇔ sin (ϕ + 45^o) = sin (ϕ’ + 45^o)

\[ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\varphi  = \varphi '}\\{\varphi  = {{90}^0} - \varphi '}\end{array}} \right.\]

Suy ra hai tam giác ABC và A’BC bằng nhau. Gọi S là tập hợp tất cả các tam giác vuông, ta có |S | = \[4C_9^2\] = 144 và S = \[\bigcup\limits_{\varphi  \in \Omega } {{S_\varphi }} \]

Trong đó \[{S_\varphi }\]là tập hợp các tam giác vuông có một góc bằng ϕ, Ω = {10^o ; 20^o ; 30^o ; 40^o}. Dễ thấy |\[{S_{{{10}^0}}}\]| = |\[{S_{{{20}^0}}}\]| = |\[{S_{{{30}^0}}}\]| = |\[{S_{{{40}^0}}}\]| = 4 · 9 = 36.

Xác suất để chọn được hai tam giác có chu vi bằng nhau là\[P = \frac{{4.C_{36}^2}}{{C_{144}^2}} = \frac{{35}}{{143}}\].

Chọn đáp án C

Câu 13. Một người rút ngẫu nhiên ra 6 quân bài từ bộ bài tú lơ khơ gồm 52 quân bài. Xác suất để rút được 6 quân bài trong đó có 1 tứ quý và 2 quân bài còn lại có chất khác nhau là

A. \[\frac{{C_{15}^1.C_{48}^1.C_{36}^1}}{{A_{52}^6}}\].

B. \[\frac{{C_{13}^1.C_4^2C_{12}^1.C_{12}^1}}{{A_{52}^6}}\].

C. \[\frac{{C_{15}^1.C_{12}^1.C_{12}^1}}{{C_{52}^6}}\].

D. \[\frac{{C_{13}^1.C_4^2.C_{12}^1.C_{12}^1}}{{C_{13}^1}}\].

Hướng dẫn giải

Gọi A là biến cố người đó bốc được 1 tứ quý và 2 quân bài còn lại có chất khác nhau. Không gian mẫu |Ω| = \[C_{52}^6\].

Bộ bài gồm có 13 tứ quý, do đó số cách chọn 1 tứ quý để người đó rút trúng là \[C_{13}^1\]. Với 1 tứ quý đã chọn, bộ bài còn lại 48 quân bài chia thành 4 chất, mỗi chất gồm 12 quân bài. Do đó, số cách chọn 2 quân bài còn lại có chất khác nhau để người đó rút trúng là \[C_4^2.C_{12}^1.C_{12}^1\].

Vì vậy |Ω_A| = \[C_{13}^1.C_4^2.C_{12}^1.C_{12}^1\].

 Do đó \[P(A) = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega  \right|}} = \frac{{C_{13}^1.C_4^2.C_{12}^1.C_{12}^1}}{{C_{13}^1}}\].

Chọn đáp án D.