Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Lý thuyết và bài tập trắc nghiệm chuyên đề tổ hợp – xác suất, tài liệu bao gồm 25 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

A. LÝ THUYẾT CƠ BẢN

I. HOÁN VỊ - TỔ HỢP - CHỈNH HỢP

1. Hoán vị

Tổng quát:

Cho tập A gồm n phần tử (n \[ \ge \]1). Khi xếp n phần tử này theo một thứ tự, ta được một hoán vị các phần tử của tập hợp A, (gọi tắt là một hoán vị của A).

Số hoán vị của một tập hợp có n phần tử là: \[{P_n} = n! = n.(n - 1).(n - 2)...3.2.1\]

2. Chỉnh hợp

Tổng quát:

Cho tập hợp A có n phần tử và cho số nguyên k, (1 £ k £ n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A, (gọi tắt là một chỉnh hợp n chập k của A).

Số các chỉnh hợp chập k của một tập hợp có n phần tử là: \[A_n^k = \frac{{n!}}{{(n - k)!}}\]

Một quy ước: 0! = 1, \[A_n^0\]= 1, \[A_n^n\] = n!.

3. Tổ hợp

Tổng quát: 

Cho tập hợp A có n phần tử và cho số nguyên k, (1 £ k £ n). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.

Số các tổ hợp chập k của một tập hợp có n phần tử là \[C_n^k = \frac{{n!}}{{(n - k)!k!}} = \frac{{A_n^k}}{{k!}}\].

Một số quy ước: với quy ước này, ta có \[C_n^0 = 1,A_n^0 = 1\], với quy ước này, ta có \[C_n^k = \frac{{n!}}{{(n - k)!k!}}\] đúng với số nguyên dương k, thỏa: 0 £ k £ n.

Tính chất: \[C_n^k = C_n^{m - k}\](0 £ k £ n) và \[C_{n + 1}^n = C_n^k + C_n^{k - 1}\], 1 £ k £ n: được gọi là hằng đẳng thức Pascal.

II. NHỊ THỨC NEWTON

1. Nhị thức Newton

\[{(a + b)^n} = \sum\limits_{k = 0}^n {C_n^k.{a^{n - k}}.{b^k} = C_n^0.{a^n} + C_n^1{a^{n - 1}}b + } C_n^2{a^{n - 2}}{b^2} + ... + C_n^{n - 1}a{b^n}.\]

2. Nhận xét:

Trong khai triển \[{(a \pm b)^n}\] có n +1 số hạng và các hệ số của các cặp số hạng cách đều số hạng đầu và số hạng cuối thì bằng nhau: \[C_n^k\]= \[C_n^{n - k}\].

Số hạng tổng quát dạng: \[{T_{n + 1}} = C_n^k.{a^{n - k}}.{b^k}\]và số hạng thứ N thì k = N – 1.

Trong khai triển (a – b)ⁿ  thì dấu đan nhau, nghĩa là +, rồi -, rồi +, ….

Số mũ của a giảm dần, số mũ của b tăng dần nhưng tổng số mũ của a và b bằng n.

Nếu trông khai triển nhị thức Newton, ta gán cho a và b những giá trị đặc biệt thì sẽ thu được những công thức đặc biệt. Chẳng hạn như:

\[{(1 + x)^n} = C_n^0{x^n} + C_n^1{x^{n - 1}} + ... + C_n^n\mathop  \to \limits^{x = 1} C_n^0 + C_n^1 + ... + C_n^n = {2^n}\]

\[{(1 - x)^n} = C_n^0{x^n} - C_n^1{x^{n - 1}} + ... + {( - 1)^n}C_n^n\mathop  \to \limits^{x =  - 1} C_n^0 - C_n^1 + ... + {( - 1)^n}C_n^n = 0\]

3. Tam giác Pascal

Các hệ số của khai triển: \[{(a + b)^0},{(a + b)^1},{(a + b)^2},...,{(a + b)^n}\]có thể xếp thành một tam giác gọi là tam giác Pascal.

III. BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ

1. Biến cố

a) Phép thử và không gian mẫu

Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà:

Kết quả của nó không đoán trước được.

Có thể xác định được tập hợp tất cả các kết quả có thể xảy ra của phép thử đó.

Tập hợp mọi kết quả của một phép thử T được gọi là không gian mẫu của T và được kí hiệu là W. Số phần tử của không gian mẫu được kí hiệu là n(W ).

b) Biến cố

Tổng quát:

Biến cố A liên quan đến phép thử T là biến cố mà việc xảy ra hay không xảy ra của A tùy thuộc vào kết quả của T.

Mỗi kết quả của phép thử T làm cho A xảy ra, được gọi là một kết quả thuận lợi cho A.

Tập hợp các kết quả thuận lợi cho A được kí hiệu là W_A

2. Xác suất

Tổng quát: Giả sử phép thử T có không gian mẫu W là một tập hữu hạn và các kết quả của T là đồng khả năng. Nếu A là một biến cố liên quan với phép thử T và W_A là một tập hợp các kết quả thuận lợi cho A thì xác suất của A là một số, kí hiệu là P (A), được xác định bởi công thức: \[P(A) = \frac{{\left| \Omega  \right|}}{{\left| {{\Omega _A}} \right|}} = \frac{{n(A)}}{{n(\Omega )}} = \frac{{So\,\,phan\,\,tu\,\,cua\,A}}{{So\,\,phan\,\,tu\,\,cua\,\,\Omega }}\].

Từ định nghĩa, suy ra: \[0 \le P(A) \le 1,P(\Omega ) = 1,P(\emptyset ) = 0.\]

IV. CÁC QUY TẮC TÍNH XÁC SUẤT

1. Quy tắc cộng xác suất

c) Biến cố hợp

Cho hai biến cố A và B. Biến cố “ A hoặc B xảy ra”, kí hiệu là A È B , được gọi là hợp của hai biến cố A và B. Khi đó: W_A È W_B Ì W

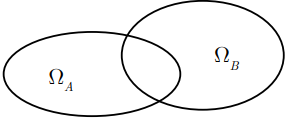
d) Biến cố xung khắc

Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra. Khi đó : W_A Ç W_B = Æ

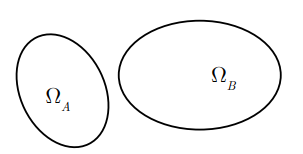
e) Quy tắc cộng xác suất hai biến cố xung khắc

Nếu A và B là biến cố xung khắc thì xác suất biến cố A È B là P(A È B) = P(A) + P (B)

Cho n biến cố A₁, A₂, …, A_n đôi một là các biến cố xung khắc với nhau.

Khi đó: P(A₁ È A₂ È A₃ È… ÈA_n) = P(A₁) + P(A₂) + P(A₃) + …+ P(A_n).

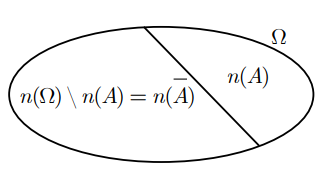
f) Biến cố đối

Cho A là một biến cố. Khi đó biến cố “không A ”, kí hiệu là \[\overline A \], được gọi là biến cố đối của A. Ta nói A và \[\overline A \]là hai biến cố đối của nhau.

Khi đó: \[{\Omega _{\overline A }} = \Omega \backslash {\Omega _A} \Rightarrow P(\overline A ) = 1 - P(A)\]

2. Quy tắc nhân xác suất

a) Biến cố giao

Cho hai biến cố A và B. Biến cố “ A và B cùng xảy ra”, kí hiệu A  Ç B hay (AB), gọi là giao của hai biến cố A và B.

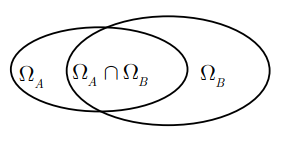
b) Hai biến cố độc lập

Hai biến cố được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng xác suất xảy ra của biến cố kia.

Nếu hai biến cố A và B độc lập với nhau thì A và \[\overline B \], \[\overline A \] và B, \[\overline A \] và \[\overline B \] cũng là độc lập.

c) Quy tắc nhân xác suất hai biến cố độc lập

Nếu A và B là hai biến cố độc lập với nhau thì ta luôn có: P(A) = P(A).P(B).

Cho n biến cố A₁,A₂,A₃,A₄, …., A_n độc lập với nhau từng đôi một. Khi đó:

\[P({A_1}{A_2}{A_3}...{A_n}) = P({A_1}).P({A_2}).P({A_3})...P({A_n})\] hay \[P\left( {\prod\limits_1^n {{A_i}} } \right) = \prod\limits_1^n P ({A_i}).\]

B. BÀI TẬP

Câu 1. Số tự nhiên n thỏa mãn \[A_n^2 - C_{n + 1}^{n - 1} = 5\]là

A. n = 3

B. n = 5

C. n = 4

D. n = 6

Câu 2: Từ các chữ số 1,2,3,4,5,6,7,8,9 , có thể lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau và lớn hơn 50000.

A. 8400

B. 15120

C. 6720

D. 3843

Câu 3: Một hộp có 5 bi đen, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi được chọn đều cùng màu là:

A. \[\frac{1}{4}\]

B. \[\frac{1}{9}\]

C.  \[\frac{4}{9}\]

D. \[\frac{5}{9}\]

Câu 4: Đội văn nghệ của nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ để biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn?

A. 120

B. 102

C. 98

D. 100

Câu 5: Với các chữ số 2,3,4,5,6 , có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau trong đó hai chữ số 2,3 không đứng cạnh nhau?

A. 120

B. 96

C. 48

D. 72

Câu 6: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau và các nam sinh luôn ngồi cạnh nhau?

A. 207360

B. 120096

C. 120960

D. 34560

Câu 7: Số 2389976875 có bao nhiêu ước số nguyên?

A. 240

B. 408

C. 204

D. 48

Câu 8: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là:

A. 24

B. 120

C. 60

D. 16

Câu 9: Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT X theo từng khối như sau: khối 10 có 5 học sinh, khối 11 có 5 học sinh và khối 12 có 5 học sinh. Nhà trường cần chọn một đội tuyển gồm 10 học sinh tham gia IOE cấp tỉnh. Tính số cách lập đội tuyển sao cho có học sinh cả ba khối.

A. 3003

B. 2509

C. 9009

D. 3000

Câu 10: Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?

A. 6

B. 16

C. 12

D. 24

Câu 11: Cho các phát biểu sau:

a) Số phần tử của tập hợp hữu hạn X được ký hiệu là |X| hoặc n(X).

b) Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của tập A Ç B bằng số phần tử của A cộng với số phần tử của B .

c) Chỉ có một quy tắc đếm cơ bản là quy tắc cộng.

d) Quy tắc cộng mở rộng là |AÈ B|= |A| + |B| - |A Ç B|.

Số đáp án đúng là?

A. 0

B. 3

C. 1

D. 2

Câu 12. Giá trị của n \[ \in \mathbb{N}\]thỏa mãn \[{P_n}A_n^2 + 72 = 6\left( {A_n^2 + 2{P_n}} \right)\]là:

A. n = 3 hoặc n = 4

B. n = 5

C. n = 2 hoặc n = 5

D. n = 6

Câu 13. Giá trị của số tự nhiên n thỏa mãn \[C_n^2 + A_n^2 = 9n\] là:

A. 7

B. 6

C. 9

D. 8

Câu 14: Giá trị của n\[ \in \mathbb{N}\]thỏa mãn \[\frac{1}{{C_n^1}} - \frac{1}{{C_{n + 1}^2}} = \frac{7}{{6C_{n + 4}^1}}\] là:

A. n = 3

B. n = 8

C. n = 5 hoặc n = 7

D. n = 3 hoặc n = 8

Câu 15: Giá trị của x\[ \in \mathbb{N}\]thỏa mãn \[C_x^1 + 6C_x^2 + 6C_x^3 = 9{x^2} - 14x\]là:

A. x = 7

B. x = 5

C. x = 11

D. x = 9

Câu 16: Giá trị của n\[ \in \mathbb{N}\]thỏa mãn \[C_{n + 1}^1 + 3C_{n + 2}^2 = C_{n + 1}^3\] là:

A. n = 12

B. n = 9

C. n = 16

D. n = 2

Câu 17: Quy tắc cộng còn có thể được phát biểu dưới dạng:

A. Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của tập A È B bằng số phần tử của A cộng với số phần tử của B .

B. Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của tập A Ç B bằng số phần tử của A cộng với số phần tử của B .

C. Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của tập A Ç B bằng số phần tử của A cộng với số phần tử của B .

D. Nếu A và B là hai tập hợp hữu hạn không hợp nhau thì số phần tử của tập A È B bằng số phần tử của A cộng với số phần tử của B .

Câu 18: Số ước số tự nhiên của số 31752000 bằng:

A. 120

B. 144

C. 256

D. 420

Câu 19: Cho tập A = { 1;2;3;4;5;6} . Từ tập A có thể lập được bao nhiêu số tự nhiên có bốn chữ số và chia hết cho 2 :

A. 648

B. 3003

C. 840

D. 3843

Câu 20: Tìm n\[ \in \mathbb{N}\] biết \[A_n^3 + 5A_n^2 = 2(n + 15)\]

A. n = 4

B. n = 3

C. n = 5

D. n = 6