Với tóm tắt lý thuyết Toán lớp 8 Bài 3: Hằng đẳng thức đáng nhớ sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.
Lý thuyết Toán lớp 8 Bài 3: Hằng đẳng thức đáng nhớ
A. Lý thuyết Hằng đẳng thức đáng nhớ
1. Bình phương của một tổng
Ví dụ:
2. Bình phương của một hiệu
Ví dụ:
3. Hiệu hai bình phương
Ví dụ:
4. Lập phương của một tổng
Ví dụ:
5. Lập phương của một hiệu
Ví dụ:
6. Tổng hai lập phương
Ví dụ:
7. Hiệu hai lập phương
Ví dụ:
Sơ đồ tư duy Hằng đẳng thức đáng nhớ.
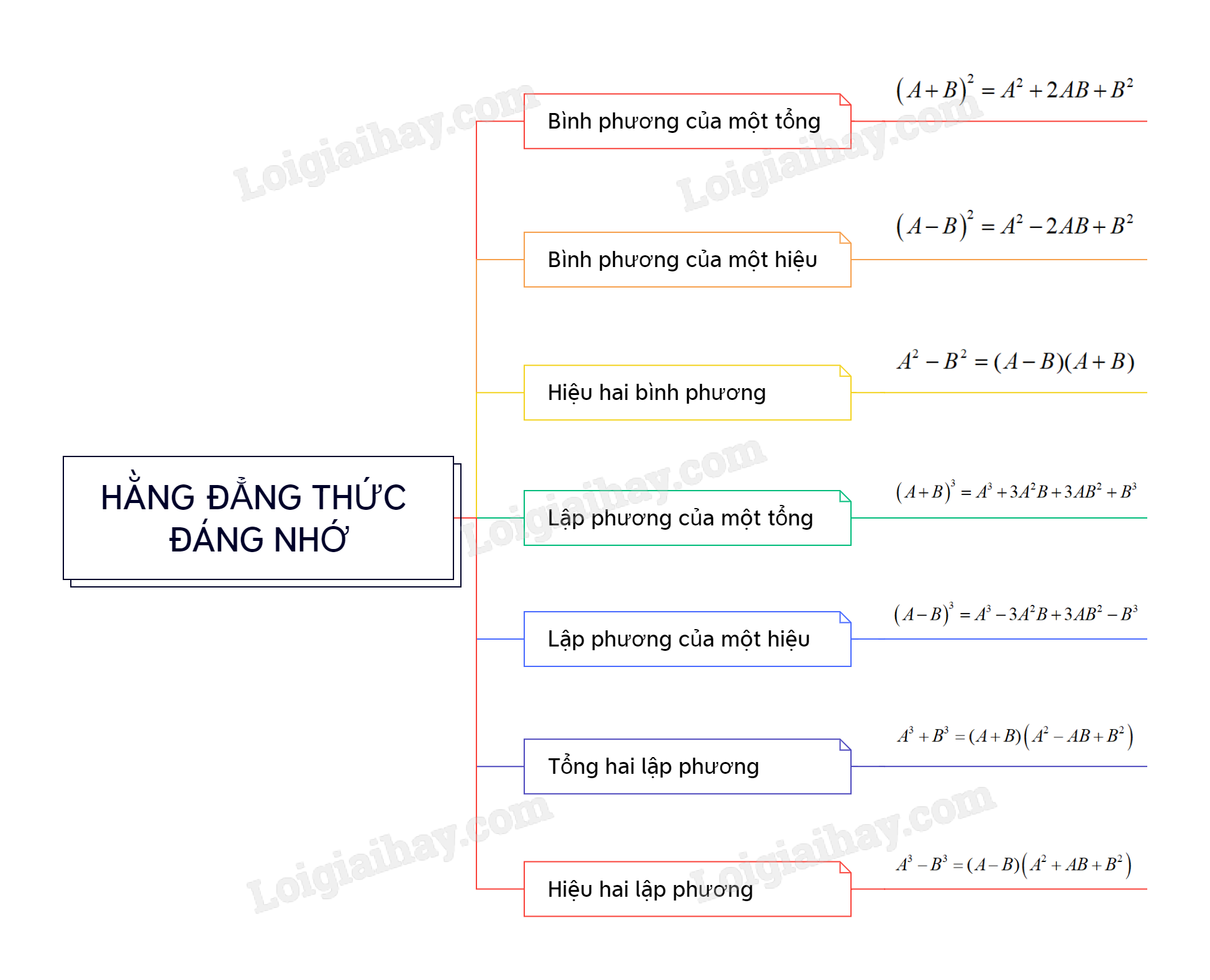
B. Bài tập Hằng đẳng thức đáng nhớ
Bài 1.Viết các biểu thức sau thành đa thức
a) (3x + 7y)2;
b) (x – 5y)2;
c) (x – 3y)(x + 3y);
d) (2a – b)(4a2 + 2ab + b2);
e) (a – 2)(a2 + 4)(a + 2);
f) (a + 5b)(a2 + 5ab + 25b2);
g) (–x + y)3;
h) (–x – xy)3.
Hướng dẫn giải
a) (3x + 7y)2
= (3x)2 + 2 . 3x . 7y + (7y)2
= 9x2 + 42xy + 49y2;
b) (x – 5y)2
= x2 – 2 . x . 5 y + (5y)2
= x2 – 10xy + 25y2;
c) (x – 3y)(x + 3y)
= x2 – (3y)2
= x2 – 9y2.
d) (2a – b)(4a2 + 2ab + b2)
= (2a – b)[(2a)2 + 2a . b + b2]
= (2a – b)3;
e) (a – 2)(a2 + 4)(a + 2)
= [(a – 2)(a + 2)](a2 + 4)
= (a2 – 4)(a2 + 4)
= (a2)2 – 42
= a4 – 16;
f) (a + 5b)(a2 + 5ab + 25b2)
= (a + 5b)[a2 + a . 5b + (5b)2]
= (a + 5b)3.
g) (–x + y)3
= (–x)3 + 3.(–x)2y + 3(–x).y2 + y3
= –x3 + 3x2y – 3xy2 + y3.
h) (–x – xy)3
= (–x)3 – 3.(–x)2xy + 3.(–x).(xy)2 – (xy)3
= –x3 – 3x3y – 3x3y2 – x3y3.
Bài 2.Viết các biểu thức sau thành bình phương hoặc lập phương của một tổng hay một hiệu:
a) 9x2 + 6x + 1;
b)
c) x3 – 3x2 + 3x – 1;
d) x3 + 9x2y + 27xy2 + 27y3.
Hướng dẫn giải
a) 9x2 + 6x + 1
= (3x)2 + 2 . 3x . 1 + 12
= (3x + 1)2;
c) x3 – 3x2 + 3x – 1
= (x – 1)3;
d) x3 + 9x2y + 27xy2 + 27y3
= x3 + 3.x2.3y + 3.x.(3y)2 + (3y)3
= (x + 3y)3.
Bài 3.Tính nhanh:
a) 982;
b) 45 . 55;
c) 672 – 332.
Hướng dẫn giải
a) 982
= (100 – 2)2
= 1002 – 2 . 100 . 2 + 22
= 10 000 – 400 + 4
= 9 604;
b) 45 . 55
= (50 – 5)(50 + 5)
= 502 – 52
= 2 500 – 25
= 2 475;
c) 672 – 332
= (67 – 33)(67 + 33)
= 34 . 100
= 3 400.
Bài 4.Cho x + y = 3, xy = 10. Tính:
a) A = x3 + y3;
b) B = (x – y)2.
Hướng dẫn giải
a) A = x3 + y3
= (x + y)(x2 – xy + y2)
= (x + y)(x2 + 2xy + y2 – 3xy)
= (x + y)[(x + y)2 – 3xy]
Thay x + y = 3, xy = 10 vào biểu thức A ta có
A = 3 . (32 – 3 . 10) = 3 . (9 – 30) = 3 . (–21) = –63.
b) B = (x – y)2
= x2 – 2xy + y2
= x2 + 2xy + y2 – 4xy
= (x + y)2 – 4xy
Thay x + y = 3, xy = 10 vào biểu thức B ta có
B = 32 – 4 . 10 = 9 – 40 = –31.
Bài 5.Cho hình lập phương có cạnh bằng 3 cm. Thể tích hình lập phương sẽ tăng bao nhiêu nếu các cạnh đều tăng a cm?
Hướng dẫn giải
Thể tích hình lập phương là
V = 3 . 3 . 3 = 27 (cm3)
Khi các cạnh đều tăng thêm a cm thì độ dài các cạnh của hình lập phương là3 + a (cm)
Thể tích hình lập phương mới là
V = (3 + a)(3 + a)(3 + a)
= (3 + a)3
= 33 + 3 . 32 . a + 3 . 3 . a2 + a3
= a3 + 9a2 + 27a + 27 (cm3)
Thể tích hình lập phương sẽ tăng thêm là
a3 + 9a2 + 27a + 27 – 27 = a3 + 9a2 + 27a (cm3)
Vậy thể tích hình lập phương sẽ tăng thêm a3 + 9a2 + 27a cm3.
Video bài giảng Toán 8 Bài 3: Hằng đẳng thức đáng nhớ - Chân trời sáng tạo
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 2: Các phép toán với đa thức nhiều biến
Lý thuyết Bài 3: Hằng đẳng thức đáng nhớ
Lý thuyết Bài 4: Phân tích đa thức thành nhân tử
Lý thuyết Bài 5: Phân thức đại số
Lý thuyết Bài 6: Cộng, trừ phân thức
Lý thuyết Bài 7: Nhân, chia phân thức