Với tóm tắt lý thuyết Toán lớp 8 Bài 4: Phân tích đa thức thành nhân tử sách Chân trời sáng tạo hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.

Lý thuyết Toán lớp 8 Bài 4: Phân tích đa thức thành nhân tử

A. Lý thuyết Phân tích đa thức thành nhân tử

1. Phân tích đa thức thành nhân tử là gì?

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

2. Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung như thế nào?

Ví dụ: Phân tích đa thức $x^3+x$ thành nhân tử: $x^3+x=x.x^2+x=x(x^2+1)$

3. Phân tích đa thức thành nhân tử bằng cách đặt nhóm hạng tử như thế nào?

Ví dụ: Phân tích đa thức $xy+3z+xz+3y$ thành nhân tử: 

$$\begin{gathered} xy+3z+xz+3y=(xy+xz)+(3z+3y) \\ =x(y+z)+3(z+y)=(x+3)(y+z) \end{gathered}$$

4. Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức như thế nào?

Ví dụ: Phân tích đa thức $x^2-8x+16$ thành nhân tử: $x^2-8x+16=x^2-2.x.4+4^2=(x-4{)}^2$

Sơ đò tư duy Phân tích đa thức thành nhân tử.

B. Bài tập Phân tích đa thức thành nhân tử

Bài 1.Phân tích các đa thức sau thành nhân tử:

a) xy + 2y².

b) (x – 1)² + 3(1 – x).

c) (y + 6)² – 4.

d) 8x² + 32xy + 32y².

e) x⁵ – x².

g) x³ – 2x² + x – 2.

h) x³ – 3y³ + 3x²y – xy².

Hướng dẫn giải

a) xy + 2y²

= y . x + y . 2y

= y(x + 2y);

b) (x – 1)² + 3(1 – x)

= (x – 1)(x – 1) – 3(x – 1)

= (x – 1)(x – 1 – 3)

= (x – 1)(x – 4).

c) (y + 6)² – 4

= (y + 6)² – 2²

= (y + 6 – 2)(y + 6 + 2)

= (y + 4)(y + 8);

d) 8x² + 32xy + 32y²

= 8(x² + 4xy + 4y²)

= 8[x² + 2 . x . 2y + (2y)²]

= 8(x + 2y)²;

e) x⁵ – x² = x² . x ³ – x²

= x²(x³ – 1)

= x²(x – 1)(x² + x + 1).

g) x³ – 2x² + x – 2

= (x³ + x) – 2(x² + 1)

= x(x² + 1) – 2(x² + 1)

= (x² + 1)(x – 2);

h) x³ – 3y³ + 3x²y – xy²

= (x³ – xy²) + (3x²y – 3y³)

= x(x² – y²) + 3y(x² – y²)

= (x² – y²)(x + 3y)

= (x – y)(x + y)(x + 3y).

Bài 2. Phân tích các đa thức sau thành nhân tử rồi tính các giá trị của nó:

a) A = a(b + 3) – b(3 + b) tại a = 2023 và b = 2017.

b) B = x² – 2x + 1 – 4y² tại x = 51 và y = 25.

c) C = x² – 3y – 3x + xy tại x = 53 và y = 47.

Hướng dẫn giải

a) A = a(b + 3) – b(3 + b)

= (b + 3)(a – b)

Thay a = 2023 và b = 2017 vào biểu thức trên ta được:

A = (2017 + 3)(2023 – 2017)

= 2020 . 6 = 12 120.

b) B = x² – 2x + 1 – 4y²

= (x² – 2x + 1) – 4y²

= (x – 1)² – 4y²

= (x – 1 – 2y)(x – 1 + 2y)

Thay x = 51 và y = 25 vào biểu thức trên ta được:

B = (51 – 1 – 2.25)(51 – 1 + 2.25)

= 0.100 = 0.

c) C = x² – 3y – 3x + xy

= (x² – 3x) + (xy – 3y)

= x(x – 3) + y(x – 3)

= (x – 3)(x + y)

Thay x = 53 và y = 47 vào biểu thức trên ta được:

C = (53 – 3)(53 + 47) = 50 . 100 = 5 000.

Bài 3. Tìm x, biết:

a) (x – 3)² = (3 + x)².

b) 1 – 9x² = (3x + 1)².

c) x²(x + 8) + x² = –8x.

d) x² – 6x + 8 = 0.

Hướng dẫn giải

a) (x – 3)² = (3 + x)²

(x – 3) – (3 + x)² = 0

(x – 3 + 3 + x)(x – 3 – 3 – x) = 0

2x.(–6) = 0

2x = 0

x = 0.

Vậy x = 0.

b) 1 – 9x² = (3x + 1)²

(1 – 3x)(1 + 3x) – (3x + 1)² = 0

(3x + 1)(1 – 3x – 3x – 1) = 0

(3x + 1)(–6x) = 0

Suy ra 3x + 1 = 0 hoặc –6x = 0

3x = –1 hoặc x = 0

$x=-\frac{1}{3}$ hoặc x = 0.

Vậy .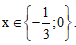

c) x²(x + 8) + x² = –8x

x²(x + 8) + x² + 8x = 0

x²(x + 8) + x(x + 8) = 0

(x + 8)(x² + x) = 0

(x + 8).x.(x + 1) = 0

Suy ra x + 8 = 0 hoặc x = 0 hoặc x + 1 = 0

x = – 8 hoặc x = 0 hoặc x = –1.

Vậy x ∈ {–8; 0; –1}.

d) x² – 6x + 8 = 0.

x² – 2x – 4x + 8 = 0

x(x – 2) – 4(x – 2) = 0

(x – 2)(x – 4) = 0

Suy ra x – 2 = 0 hoặc x – 4 = 0

x = 2 hoặc x = 4.

Vậy x ∈ {2; 4}.

Bài 4.Cho x > 0. Tìm độ dài cạnh hình vuông có diện tích bằng 36x² + 60x + 25.

Hướng dẫn giải

Gọi cạnh hình vuông là a (a > 0)

Khi đó diện tích hình vuông là a²

Tức là 36x² + 60x + 25= a².

Ta sẽ phân tích đa thức 36x² + 60x + 25thành nhân tử có dạng a².

Ta có:

36x² + 60x + 25 = (6x)² + 2 . 6x . 5 + 5² = (6x + 5)²

Suy ra a² = (6x + 5)²

Do đó a = 6x + 5

Vậy độ dài cạnh hình vuông có diện tích bằng 36x² + 60x + 25 là 6x + 5.

Video bài giảng Toán 8 Bài 4: Phân tích đa thức thành nhân tử - Chân trời sáng tạo

Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3: Hằng đẳng thức đáng nhớ

Lý thuyết Bài 4: Phân tích đa thức thành nhân tử

Lý thuyết Bài 5: Phân thức đại số

Lý thuyết Bài 6: Cộng, trừ phân thức

Lý thuyết Bài 7: Nhân, chia phân thức

Lý thuyết Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều