Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 5: Phép chiếu song song chi tiết sách Toán 11 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 5: Phép chiếu song song
Lời giải:
Bóng của biển này có dạng hình bình hành.
+) Ta có: mp(AA’D’D) // mp(BB’C’C)
Mặt đất cắt các mp(AA’D’D) và mp(BB’C’C) lần lượt tại các giao tuyến A’D’ và B’C’. Do đó A’D’ // B’C’ (1).
+) Ta lại có: mp(ABB’A’) // mp(DD’C’C)
Mặt đất cắt các mp(ABB’A’) và mp(DD’C’C) lần lượt tại các giao tuyến A’B’ và D’C’. Do đó A’B’ // D’C’ (2).
Từ (1) và (2) ta có A’B’C’D’ là hình bình hành.
1. Khái niệm phép chiếu song song
Hoạt động khám phá 1 trang 121 Toán 11 Tập 1: Trong hoạt động khởi động:
a) Các tia sáng AA’, BB’, DD’ có song song với nhau hay không?
b) Nêu cách xác định bóng C’ của điểm C trên mặt đường.
Lời giải:
a) Các tia sáng AA’, BB’ và DD’ song song với nhau.
b) Cách xác định bóng C’ của điểm C trên mặt đường như sau:
Từ A kẻ tia sáng song song theo phương l cắt mặt đất tại điểm A’.
Từ B kẻ tia sáng song song theo phương l cắt mặt đất tại điểm B’.
Từ C kẻ tia sáng song song theo phương l cắt mặt đất tại điểm C’.
Từ D kẻ tia sáng song song theo phương l cắt mặt đất tại điểm D’.
Vậy ta có bóng của biển báo là hình bình hành A’B’C’D’.
Lời giải:
Quan sát hình vẽ trên, ta được:
+) Phương chiếu là đường thẳng a;
+) Mặt phẳng chiếu là mặt phẳng (Q).
Lời giải:
Ảnh của hình hộp ABEF.DCGH qua phép chiếu có phương chiếu l là hình hộp C’D’H’G’.B’A’F’E’.
2. Các tính chất cơ bản của phép chiếu song song
a) Khi điểm M thay đổi trên đường thẳng a thì ảnh M’ của nó thay đổi ở đâu?
b) Từ đó hãy chỉ ra ảnh của đường thẳng a qua phép chiếu theo phương l lên mặt phẳng (P).
Lời giải:
a) Khi điểm M thay đổi trên đường thẳng a thì ảnh M’ của nó thay đổi ở trên đường thẳng a’.
b) Ảnh của đường thẳng a qua phép chiếu theo phương l lên mặt phẳng (P) là đường thẳng a’.
Lời giải:
Hình 5a): Trong trường hợp (Q) // (R) thì hình chiếu a’ // b’.
Hình 5b): Trong trường hợp (Q) ≡ (R) thì hình chiếu a’ ≡ b’.
Lời giải:
Hình chiếu song song của hình thang ABCD là tứ giác A’B’C’D’. Vì AB // CD và nên theo tính chất phép chiếu song song thì A’B’ // C’D’ và hay A’B’ = 2C’D’.
Lời giải:
+) Ta có:
Hình chiếu của B là B’
Hình chiếu của C là C’
Hình chiếu của M là M’
Suy ra:
B, M, C thẳng hàng nên B’, M’, C’ thẳng hàng
hay B’M’ = C’M’
Vì vậy M’ là trung điểm của B’C’.
+) Ta lại có:
Hình chiếu của A là A’
Hình chiếu của M là M’
Hình chiếu của G là G’
Suy ra:
A, G, M thẳng hàng nên A’, G’, M’ thẳng hàng
A’M’ là đường trung tuyến của tam giác A’B’C’ nên G’ là trọng tâm tam giác A’B’C’.
3. Hình biểu diễn của một hình không gian
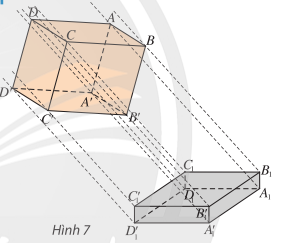
Lời giải:
Dựa vào quan sát Hình 7, ta thấy hình chiếu của hình hộp chữ nhật trên nền nhà là một hình hộp chữ nhật khác đồng dạng với hình hộp chữ nhật ban đầu.
Lời giải:
Hình 10a) là hình biểu diễn của hình hộp chữ nhật.
Hình 10b) là hình biểu diễn của hình lăng trụ đứng tam giác.
Hình 10c) là hình biểu diễn của hình chóp tứ giác.
Lời giải:
Bài tập
Bài 1 trang 126 Toán 11 Tập 1: Trong các mệnh đề sau, mệnh đề nào đúng?
a) Một đường thẳng có thể song song với hình chiếu của nó;
b) Một đường thẳng có thể trùng với hình chiếu của nó;
c) Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau;
d) Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.
Lời giải:
a) Mệnh đề này đúng
b) Mệnh đề này đúng
c) Mệnh đề này đúng
d) Mệnh đề này đúng
Bài 2 trang 126 Toán 11 Tập 1: Vẽ hình biểu diễn của một lục giác đều.
Lời giải:
Bài 3 trang 126 Toán 11 Tập 1: Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn.
Lời giải:
Vẽ tam giác ABC là hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn. Qua O ta kẻ hai dây ME và NF của elip lần lượt song song với AC và AB. Khi đó tứ giác MNEF là hình biểu diễn của một hình vuông nội tiếp trong một đường tròn.
a) A’B’ = AB;
b) A’B’ = 2AB.
Lời giải:
Phép chiếu theo đường thẳng d tới mp(α) biến:
Điểm A thành điểm A’;
Điểm B thành điểm B’;
Điểm O thành chính điểm O.
Mà ba điểm A, B, O thằng hàng nên A’, B’, O thẳng hàng.
a) Để A’B’ = AB thì đường thẳng d phải vuông góc với (α).
b) Để A’B’ = 2AB thì
Bài 5 trang 126 Toán 11 Tập 1: Vẽ hình biểu diễn của:
a) Hình lăng trụ có đáy là tam giác đều;
b) Hình lăng trụ có đáy là lục giác đều;
c) Hình hộp.
Lời giải:
a)
+) Hình biểu diễn của mặt đáy là tam giác, hình biểu diễn của mặt bên là các hình bình hành.
b)
Hình biểu diễn của mặt đáy là lục giác có các cặp cạnh đối song song và bằng nhau, đồng thời song song với đường chéo nối hai đỉnh còn lại. Hình biểu diễn của mặt bên là các hình bình hành.
c)
Hình biểu diễn của các mặt là hình bình hành.
Xem thêm các bài giải SGK Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm
Lý thuyết Phép chiếu song song
1. Khái niệm phép chiếu song song
- Trong không gian, cho mặt phẳng và đường thẳng cắt . Phép đặt tương ứng mỗi điểm M trong không gian với điểm M’ của mặt phẳng sao cho MM’ song song hoặc trùng với được gọi là phép chiếu song song lên mặt phẳng theo phương .
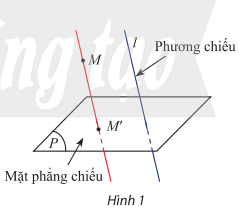
- Mặt phẳng gọi là mặt phẳng chiếu, đường thẳng gọi là phương chiếu, điểm M’ gọi là hình chiếu song song (hoặc ảnh) của điểm M qua phép chiếu theo phương .
- Cho hình , tập hợp các ảnh M’ của tất cả những điểm M thuộc qua phép chiếu song song được gọi là hình chiếu song song của lên mặt phẳng (P).
2. Các tính chất cơ bản của phép chiếu song song
- Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng, biến tia thành tia.
- Phép chiếu song song biến 2 đường thẳng song song thành 2 đường thẳng song song hoặc trùng nhau.
- Phép chiếu song song biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không làm thay đổi thứ tự 3 điểm đó.
- Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng cùng nằm trên hai đường thẳng song song hoặc trùng nhau.
3. Hình biểu diễn của một hình không gian
Hình biểu diễn của một hình không gian là hình chiếu song song của hình đó trên một mặt phẳng theo phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Quy tắc vẽ hình biểu diễn:
- Nếu trên hình có 2 đoạn thẳng nằm trên 2 đường thẳng song song (trùng nhau) thì chúng được biểu diễn bằng 2 đoạn thẳng nằm trên 2 đường thẳng song song (trùng nhau) và tỉ số độ dài của 2 đoạn thẳng không đổi.
- Nếu hình phẳng nằm trong mặt phẳng không song song với phương chiếu thì:
+ Hình biểu diễn của một đường tròn là một elip.
+ Hình biểu diễn của một tam giác (vuông, cân, đều) là một tam giác.
+ Hình biểu diễn của hình vuông, hình chữ nhật, hình thoi, hình bình hành là hình bình hành.