Với giải Luyện tập 1 trang 110 Toán lớp 8 Tập 1 Cánh diều chi tiết trong Bài 5: Hình chữ nhật giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Giải bài tập Toán lớp 8 Bài 5: Hình chữ nhật
Luyện tập 1 trang 110 Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC. Chứng minh .
Lời giải:
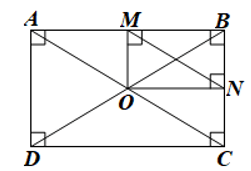
Do M, N lần lượt là hình chiếu của O trên AB, BC nên OM ⊥ AB và ON ⊥ BC.
Xét tứ giác OMBN có .
Do đó tứ giác OMBN là hình chữ nhật.
Suy ra OB = MN.
Do ABCD là hình chữ nhật nên OB = OD =
Khi đó .
Vậy .
Lý thuyết Tính chất
Trong một hình chữ nhật:
- Hai cạnh đối song song và bằng nhau;
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Ví dụ: Cho hình chữ nhật ABCD và hình bình hành ABEC.
Chứng minh BD = BE.
Hướng dẫn giải
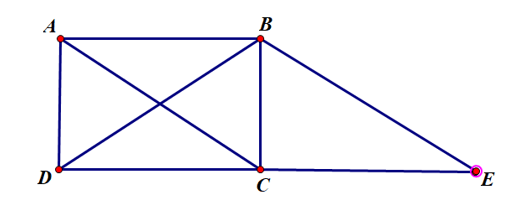
Ta có: ABCD là hình chữ nhật nên AC = BD;
ABEC là hình bình hành nên BE = AC.
Suy ra BD = BE (vì cùng bằng AC).
Vậy BD = BE.
Xem thêm các lời giải bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Khởi động trang 109 Toán 8 Tập 1:....
Hoạt động 1 trang 109 Toán 8 Tập 1: Cho biết số đo mỗi góc của tứ giác ABCD ở Hình 47....
Hoạt động 2 trang 109 Toán 8 Tập 1: a) Mỗi hình chữ nhật có là một hình thang cân hay không?...
Xem thêm các bài giải SGK Toán lớp 8 Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
