Với tóm tắt lý thuyết Toán lớp 11 Bài 17: Hàm số liên tục sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 11.

Lý thuyết Toán lớp 11 Bài 17: Hàm số liên tục

A. Lý thuyết Hàm số liên tục

1. Hàm số liên tục tại 1 điểm

 Cho hàm $y=f(x)$ xác định trên khoảng $\left(a;b\right)$chứa điểm $x_0$. Hàm số $f(x)$ được gọi là liên tục tại điểm $x_0$ nếu $\underset{x\to x_0}{lim}f(x)=f(x_0)$.

 Hàm số không liên tục tại $x_0$ được gọi là gián đoạn tại điểm đó.

2. Hàm số liên tục trên một khoảng

- Hàm số $y=f(x)$ được gọi là liên tục trên khoảng $\left(a;b\right)$ nếu nó liên tục tại mọi điểm thuộc khoảng này.

- Hàm số $y=f(x)$ được gọi là liên tục trên đoạn $\left[a;b\right]$nếu nó liên tục trên khoảng $\left(a;b\right)$ và $\underset{x\to a^{+}}{lim}f(x)=f(a),\underset{x\to b^{-}}{lim}f(x)=f(b)$.

*Nhận xét:

- Hàm số đa thức và hàm số $y=\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x},y=c\mathrm{o}\mathrm{s}\mathrm{x}$ liên tục trên $\mathbb{R}$.

- Các hàm số $y=\tan \mathrm{x},y=c\mathrm{o}\mathrm{t}\mathrm{x},y=\sqrt{x}$ và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.

3. Một số tính chất cơ bản

Giả sử hai hàm số $y=f(x)$ và $y=g(x)$ liên tục tại điểm $x_0$. Khi đó:

a, Các hàm số $y=f(x)\pm g(x)$ và $y=f(x).g(x)$ liên tục tại điểm $x_0$.

b, Hàm số $y=\frac{f(x)}{g(x)}$ liên tục tại điểm $x_0$nếu $g(x_0)\ne 0$.

Sơ đồ tư duy Hàm số liên tục.

B. Bài tập Hàm số liên tục

Bài 1: Cho hàm số f(x) = 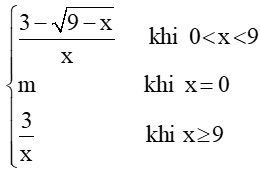. Tìm giá trị của m để f(x) liên tục trên [0; +∞).

Hướng dẫn giải

+) Với x ∈ (0; 9): f(x) = $\frac{3-\sqrt{9-x}}{x}$ liên tục trên (0; 9).

+) Với x ∈ [9; +∞) thì f(x) = $\frac{3}{x}$ liên tục trên [9; +∞).

+) Tại x = 0 ta có f(0) = m

Vậy để hàm số liên tục trên [0; +∞) khi nó phải liên tục tại x = 0.

Suy ra: $\underset{x\to 0^{+}}{\lim }$f(x) = m$\Rightarrow$m = $\frac{1}{6}$.

Vậy m = $\frac{1}{6}$ thì f(x) liên tục trên [0; +∞).

Bài 2: Cho hàm số f(x) = 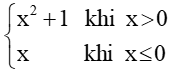. Xét tính liên tục của hàm số tại x = 0.

Hướng dẫn giải

Ta có: f(0) = 0

$\underset{x\to 0^{+}}{\lim }$f(x) = $\underset{x\to 0^{+}}{\lim }$(x²+1) = 1

$\underset{x\to 0^{-}}{\lim }$f(x) = $\underset{x\to 0^{-}}{\lim }$x = 0

Vậy f(x) gián đoạn tại x = 0.

Bài 3: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 3 và $\underset{x\to 1}{\lim }$[2f(x)-g(x)] = 4. Tính g(1).

Hướng dẫn giải

Vì hàm số f(x) liên tục tại x = 1 nên hàm số 2f(x) cũng liên tục tại x = 1.

Mà hàm số g(x) liên tục tại x = 1. Do đó, hàm số y = 2f(x) – g(x) liên tục tại x = 1.

Suy ra: $\underset{x\to 1}{\lim }$[2f(x)-g(x)] = 2f(1) – g(1) = 4

Mà f(1) = 3 nên ta có: 2 . 3 – g(1) = 4, suy ra g(1) = 2.

Vậy g(1) = 2.

Video bài giảng Toán 11 Bài 17: Hàm số liên tục - Kết nối tri thức

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 16: Giới hạn của hàm số

Lý thuyết Bài 17: Hàm số liên tục

Xem thêm các bài tóm tắt lý thuyết chương Toán lớp 11 Kết nối tri thức hay, chi tiết khác

Lý thuyết Chương 1: Hàm số lượng giác và phương trình lượng giác

Lý thuyết Chương 2: Dãy số. Cấp số cộng và cấp số nhân

Lý thuyết Chương 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu ghép nhóm

Lý thuyết Chương 4: Quan hệ song song trong không gian

Lý thuyết Chương 5: Giới hạn. Hàm số liên tục