Với Giải toán lớp 6 trang 15 Tập 2 Chân trời sáng tạo tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6. Mời các bạn đón xem:
Giải Toán 6 trang 15 Tập 2 Chân trời sáng tạo
Bài 1 trang 15 Toán lớp 6 Tập 2: So sánh hai phân số.
a) 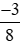 và
và 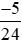 ;
;
b) 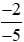 và
và 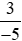 ;
;
c) 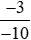 và
và 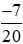 ;
;
d) 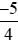 và
và 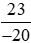 .
.
Lời giải:
a) 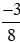 và
và 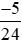 .
.
Mẫu số chung: 24.
Ta thực hiện: 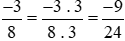 và giữ nguyên phân số
và giữ nguyên phân số 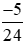 .
.
Vì −9 < −5 nên 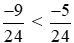 .
.
Do đó 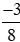 <
< 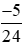 .
.
Vậy 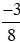 <
< 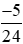 .
.
b) 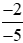 và
và 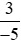
Cách 1: (Đưa hai phân số về cùng mẫu dương rồi so sánh tử số của hai phân số đó).
Đưa hai phân số về cùng mẫu dương, ta được:
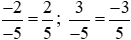
Vì −2 > −3 nên 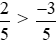
Vậy 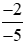 >
> 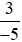 .
.
Cách 2: (So sánh hai phân số đó với 0 và áp dụng tính chất bắc cầu).
Ta có: 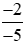 > 0 (phân số có tử số và mẫu số cùng dấu)
> 0 (phân số có tử số và mẫu số cùng dấu)
Và 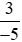 < 0 (phân số có tử số và mẫu số trái dấu).
< 0 (phân số có tử số và mẫu số trái dấu).
Áp dụng tính chất bắc cầu, ta suy ra: 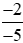 >
>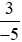 .
.
Vậy 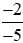 >
> 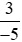 .
.
c) 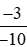 và
và 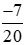
Cách 1: (Đưa hai phân số về cùng mẫu dương rồi so sánh tử số của hai phân số đó).
Ta có: 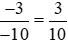 .
.
Mẫu số chung của hai phân số 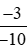 và
và 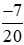 là 20.
là 20.
Ta thực hiện: 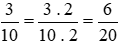 và
và 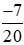 .
.
Vì 6 > −7 nên 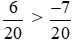 hay
hay 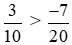 .
.
Vậy 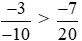 .
.
Cách 2: (So sánh hai phân số đó với 0 và áp dụng tính chất bắc cầu).
Ta có: 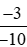 > 0 (phân số có tử số và mẫu số cùng dấu)
> 0 (phân số có tử số và mẫu số cùng dấu)
Và 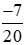 < 0 (phân số có tử số và mẫu số trái dấu).
< 0 (phân số có tử số và mẫu số trái dấu).
Áp dụng tính chất bắc cầu, ta suy ra: 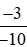 >
> 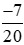 .
.
Vậy 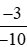 >
> 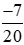 .
.
d) 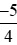 và
và 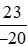
Ta có: 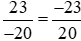
Mẫu số chung của hai phân số 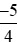 và
và 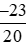 là 20.
là 20.
Ta thực hiện: 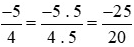 và giữ nguyên phân số
và giữ nguyên phân số 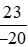 .
.
Vì −25 < −23 nên 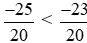 hay
hay 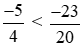 .
.
Vậy 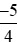 <
< 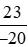 .
.
Bài 2 trang 15 Toán lớp 6 Tập 2: Tổ 1 gồm 8 bạn có tổng chiều cao là 115 dm. Tổ 2 gồm 10 bạn có tổng chiều cao là 138 dm. Hỏi chiều cao trung bình của các bạn ở tổ nào lớn hơn?
Lời giải:
Trung bình chiều cao của mỗi bạn ở tổ 1 là:
115 : 8 = 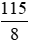 (dm)
(dm)
Trung bình chiều cao của mỗi bạn ở tổ 2 là:
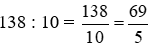 (dm)
(dm)
Ta có: 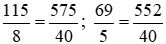 .
.
Vì 575 > 552 nên 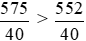 hay
hay 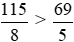 .
.
Vậy chiều cao trung bình của các bạn tổ 1 lớn hơn.
Bài 3 trang 15 Toán lớp 6 Tập 2: a) So sánh 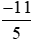 với
với 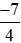 với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
với –2 bằng cách viết –2 ở dạng phân số có mẫu số thích hợp.
Từ đó suy ra kết quả so sánh 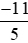 với
với 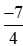 .
.
b) So sánh 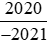 với
với 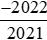 .
.
Lời giải:
a) Ta có: −2 = 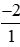 .
.
Mẫu số thích hợp để so sánh 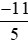 với
với 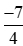 với –2 là mẫu số chung của ba phân số
với –2 là mẫu số chung của ba phân số 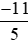 ;
; 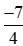 và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
và −2 (ta nên tìm mẫu chung nhỏ nhất để phân số sau khi quy đồng đơn giản nhất có thể).
Mẫu số chung là 20.
Ta thực hiện:
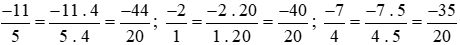
Vì −44 < −40 nên 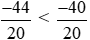 hay
hay 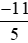 < −2.
< −2.
Vì −40 < −35 nên 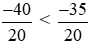 hay −2 <
hay −2 <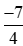 .
.
Áp dụng tính chất bắc cầu, ta suy ra: < .
Vậy 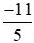 <
<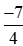 .
.
b) So sánh 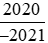 với
với 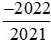 .
.
Nhận thấy: 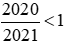 và
và 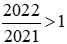 .
.
Do đó để so sánh hai phân 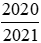 và
và 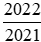 , ta có thể so sánh chúng với 1.
, ta có thể so sánh chúng với 1.
Suy ra ta có thể so sánh hai phân số 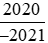 với
với 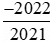 với −1.
với −1.
Cách 1: So sánh hai phân số trên với −1 và áp dunng tính chất bắc cầu.
Ta có: 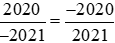
Vì 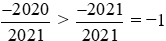
Và 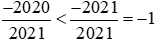
Do đó áp dụng tính chất bắc cầu, ta suy ra: 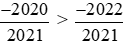 .
.
Vậy 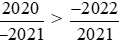 .
.
Cách 2: Đưa hai phân số về cùng mẫu dương rồi so sánh:
Ta có: 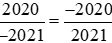 .
.
Vì −2020 > −2022 nên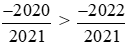 .
.
Vậy 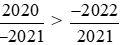 .
.
Bài 4 trang 15 Toán lớp 6 Tập 2: Sắp xếp các số 2; 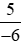 ;
; 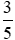 ; −1;
; −1; 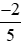 ; 0 theo thứ tự tăng dần.
; 0 theo thứ tự tăng dần.
Lời giải:
Để sắp xếp các phân số theo thứ tự tăng dần hoặc giảm dần, ta làm như sau:
Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.
+ Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.
+ Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.
Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).
Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần hoặc giảm dần (phân số âm luôn bé hơn phân số dương).
a) Ta có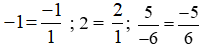 .
.
+ Nhóm các phân số dương: 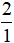 ;
; .
.
+ Nhóm các phân số âm: 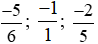
Ta so sánh các phân số trong cùng nhóm với nhau:
+ + Nhóm các phân số dương:  và
và 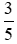
Mẫu số chung: 5.
Ta thực hiện: 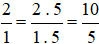 và giữ nguyên phân số
và giữ nguyên phân số 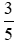 .
.
Vì 5 > 10 nên 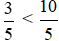 hay
hay 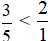 .
.
+ So sánh 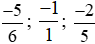 .
.
Mẫu số chung: 30.
Ta thực hiện: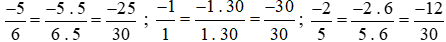
Vì −30 < −25 < −12 nên 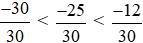 hay
hay 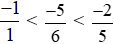 .
.
Từ đó, suy ra 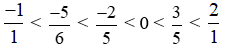
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: −1; 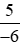 ;
; 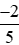 ; 0;
; 0; 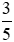 ; 2.
; 2.
Xem thêm các bài giải Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác: