Với giải sách bài tập Toán 6 Bài 3: So sánh phân số sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 3: So sánh phân số
Bài 1 trang 16 sách bài tập Toán lớp 6 Tập 2: So sánh hai phân số:
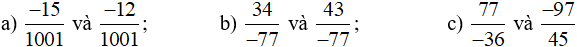
Lời giải:
Để So sánh hai phân số bằng cách đưa về cùng mẫu số thì ta thực hiện theo hai bước sau:
Bước 1: Viết hai phân số về dạng hai phân số có cùng một mẫu số dương.
Bước 2: So sánh tử số, phân số nào có tử nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
a) Hai phân số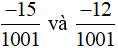 
có cùng một mẫu số dương nên ta so sánh tử số của hai phân số đó.
Vì −15 < −12 nên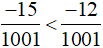 
.
Vậy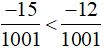 
.
b) Đưa hai phân số về cùng một mẫu số dương: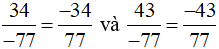 
Vì −34 > −43 nên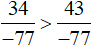 
.
Vậy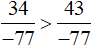 
.
c) Đưa hai phân số về cùng một mẫu số dương bằng cách quy đồng mẫu số hai phân số:
Mẫu số chung: 180.
Ta thực hiện:
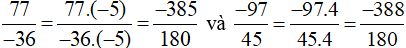
Vì −385 > −388 nên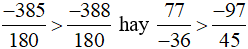 
Vậy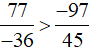 
Bài 2 trang 16 sách bài tập Toán lớp 6 Tập 2: So sánh:
Lời giải:
Để So sánh: một số nguyên và một phân số, ta có thể làm theo hai cách sau:
Cách 1: Đưa số nguyên về dạng phân số có cùng mẫu dương với phân số và phân số có mẫu số dương, rồi So sánh:tử số của hai phân số.
Cách 2: Đưa số nguyên về dạng phân số có mẫu số là 1, tử số là số nguyên đó, sau đó tiến hành quy đồng mẫu số hai phân số (đưa hai phân số về cùng một mẫu số dương).
a) Cách 1: Ta có: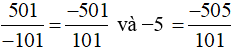 
Vì −501 > −505 nên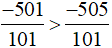 
.
Vậy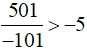 
.
Cách 2: Ta có: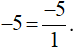 
Quy đồng mẫu số hai phân số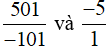 
, ta được:
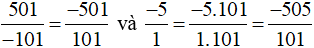
Vì −501 > −505 nên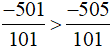 
.
Vậy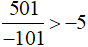 
.
b) −12 và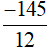 
Cách 1: Ta có: −12 =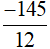 
.
Vì −144 > −145 nên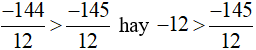 
.
Vậy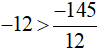 
.
Cách 2: Ta có: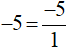 
.
Quy đồng mẫu số hai phân số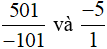 
, ta được:
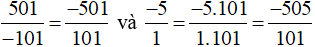
Vì −501 > −505 nên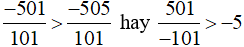 
Vậy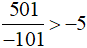 
.
Bài 3 trang 16 sách bài tập Toán lớp 6 Tập 2: Sắp xếp các số theo thứ tự
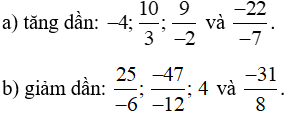
Lời giải:
Để sắp xếp các phân số theo thứ tự tăng dần hoặc giảm dần, ta làm như sau:
Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.
+ Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.
+ Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.
Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).
Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần hoặc giảm dần (phân số âm luôn bé hơn phân số dương).
a) Ta có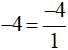 
.
+ Các phân số dương: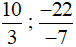 
+ Các phân số âm: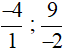 
.
Ta so sánh các phân số dương với nhau, các phân số âm với nhau:
+ So sánh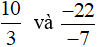 
Mẫu số chung: 21.
Ta thực hiện: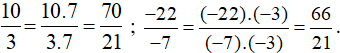 
Vì 70 > 66 nên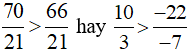 
+ So sánh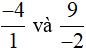 
Mẫu số chung: 2.
Ta thực hiện: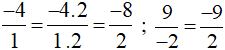 
Vì −8 > −9 nên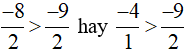 
Từ đó, suy ra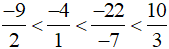 
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: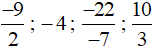 
b) Ta có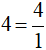 
.
+ Các phân số dương: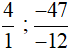 
+ Các phân số âm: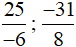 
Ta so sánh các phân số dương với nhau, các phân số âm với nhau:
+ So sánh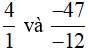 
Mẫu số chung: 12.
Ta thực hiện: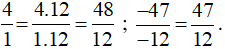 
Vì 48 > 47 nên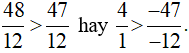 
+ So sánh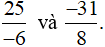 
Mẫu số chung: 24.
Ta thực hiện: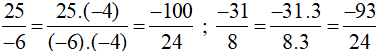 
Vì −100 < −93 nên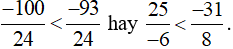 
Từ đó, suy ra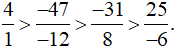 
Vậy ta sắp xếp được theo thứ tự giảm dần như sau: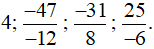 
Bài 4 trang 16 sách bài tập Toán lớp 6 Tập 2: Khẳng định sau đúng hay sai? Vì sao?
Lời giải:
Đưa hai phân số về cùng mẫu dương rồi so sánh tử số, sau đó kiểm tra khẳng định đó đúng hay sai.
a) Mẫu số chung: 30.
Ta thực hiện: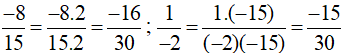 
Vì −16 < −15 nên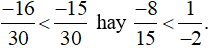 
Vậy khẳng định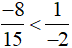 
đúng.
b) Mẫu số chung: 12.
Ta thực hiện: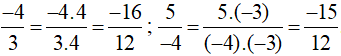 
Vì −16 < −15 nên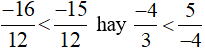 
Vậy khẳng định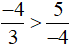 
sai.
Bài 5 trang 16 sách bài tập Toán lớp 6 Tập 2: Tìm số nguyên x thỏa mãn:
Lời giải:
Đưa các phân số về cùng mẫu dương để so sánh tử số, sau đó tìm các số nguyên x thỏa mãn.
a) Ba phân số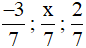 
có cùng mẫu dương nên:
Để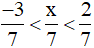 
thì −3 < x < 2.
Các số nguyên x thoả mãn lớn hơn −3 nhỏ hơn 2 là: −2; −1; 0; 1.
Vậy số nguyên x thỏa mãn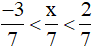 
là −2; −1; 0; 1.
b)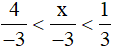 
Ta có: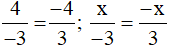 
Viết lại như sau: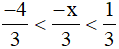 
.
Phân số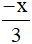 
có cùng mẫu số dương với hai phân số 
.
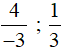Do đó để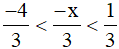 
thì −4 < −x < 1 suy ra 4 > x > −1.
Các số nguyên x thỏa mãn – 1 < x < 4 là: 0; 1; 2; 3.
Vậy số nguyên x thỏa mãn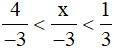 
là 0; 1; 2; 3.
Lời giải:
Bài toán đưa về sắp xếp các phân số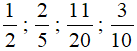 
theo thứ tự tăng dần hoặc giảm dần. Sau đó tìm môn thi đấu được học sinh đăng kí nhiều nhất và ít nhất.
Quy đồng mẫu số các phân số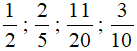 
, ta được:
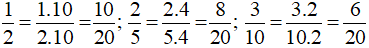; giữ nguyên phân số 
.
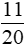Vì 6 < 8 < 10 < 11 nên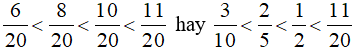 
Vậy môn thể thao được kí nhiều nhất tương ứng với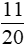 
số học sinh đăng kí thi đấu là kéo co; môn thể thao được kí ít nhất tương ứng với 
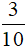số học sinh đăng kí thi đấu là cầu lông.
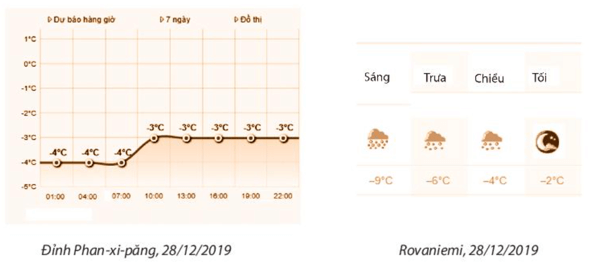
a) Số đo nhiệt độ trung bình trong ngày 28/12/2019 ở đỉnh Phan-xi-păng và ở Rovaniemi là hai phân số nào?
b) So sánh hai phân số ở câu a) và cho biết ý nghĩa thực tiễn của kết quả so sánh.
Lời giải:
a) Từ thông tin có trong hình, ta thấy nhiệt độ trung bình trong ngày 28/12/2019 ở đỉnh Phan-xi-păng là trung bình cộng của nhiệt độ tại 8 thời điểm, còn nhiệt độ trung bình tại Rovaniemi là trung bình cộng tại 4 thời điểm.
Trung bình cộng của nhiệt độ tại 8 thời điểm ở Phan-xi-păng là:
[(−4) + (−4) + (−4) + (−3) +(−3) + (−3) + (−3) + (−3)] : 8
= [(−4) . 3 + (−3) . 5] : 8 =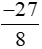 
(oC).
Trung bình cộng nhiệt độ tại 4 thời điểm ở Rovaniemi là:
[(−9) + (−6) + (−4) + (−2)] : 4 =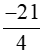 
(oC).
Vậy phân số biểu thị nhiệt độ trung bình ở đỉnh Phan-xi-păng và Rovaniemi lần lượt l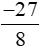à 
và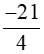 
.
b) Ta có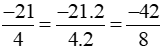 
.
Vì -42 < -27 nên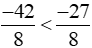 
nên nhiệt độ trung bình ngày 28/12/2019 tại Rovaniemi thấp hơn ở đỉnh Phan-xi-păng.
Ý nghĩa thực tiễn: Ngày 28/12/2019, ở Rovaniemi lạnh hơn ở đỉnh Phan-xi-păng.
b) Số nguyên m có điều kiện gì thì phân số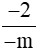 
là phân số âm?
Lời giải:
Phân số dương là phân số lớn hơn 0 (hay phân số có tử số và mẫu số cùng dấu).
Phân số âm là phân số nhỏ hơn 0 (hay phân số có tử số và mẫu số trái dấu).
a) Cách 1: Ta có: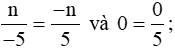 
Để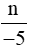 
là phân số dương thì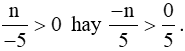 
Khi đó −n > 0 suy ra n < 0.
Vậy n là số nguyên âm thì phân số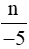 
là phân số dương.
Cách 2: Để phân số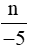 
là phân số dương thì n và −5 là hai số nguyên cùng dấu.
Mà số −5 mang dấu trừ (−) nên n mang trừ (−).
Vậy n là số nguyên âm thì phân số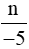 
là phân số dương.
b) Cách 1: Ta có: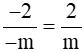 
Để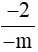 
là phân số âm thì 
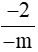< 0 hay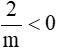 
Vì 2 > 0 nên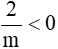 
khi m < 0.
Vậy m là số nguyên âm thì phân số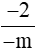 
là phân số âm.
Cách 2: Để phân số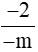 
là phân số âm thì −2 và −m là hai số nguyên trái dấu.
Mà số −2 mang dấu trừ (−) nên −m mang cộng (+) hay m mang dấu trừ (−).
Vậy m là số nguyên âm thì phân số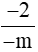 
là phân số âm.
Lý thuyết So sánh phân số
1. So sánh hai phân số có cùng mẫu
Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 1. So sánh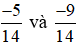 
.
Lời giải:
Ta có −5 > −9 và 14 > 0 nên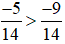 
.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ 2. So sánh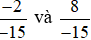 
.
Lời giải:
Đưa hai phân số về cùng mẫu dương, ta được:
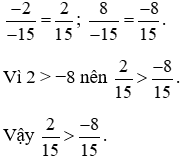
2. So sánh hai phân số khác mẫu
Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.
Ví dụ 3. So sánh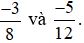 
.
Lời giải:
Mẫu số chung = BCNN (8; 12) = 24.
Ta thực hiện
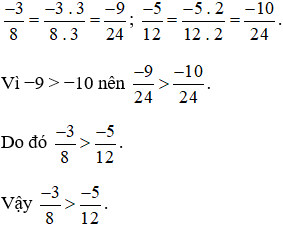
3. Áp dụng quy tắc so sánh phân số
Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.
Ví dụ 4. Viết số nguyên dưới dạng phân số rồi so sánh hai số sau: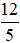 
và 3.
Lời giải:
a) Ta có: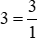 
.
Mẫu số chung là: 5.
Ta thực hiện: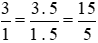 
và giữ nguyên phân số .
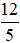Vì 15 > 12 nên
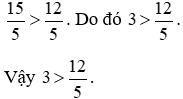
Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là:
Nếu có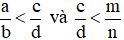 
thì ta có 
.
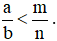Ví dụ 5. So sánh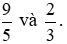 
.
Lời giải:
Phân số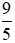 
có tử số là 9 lớn hơn mẫu số là 5 nên 
.
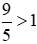Phân số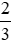 
có tử số là 2 nhỏ hơn mẫu số là 3 nên 
.
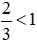Do đó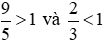 
.
Theo tính chất bắc cầu, ta suy ra:
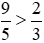
Nhận xét:
- Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.
- Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.
Ví dụ 6. So sánh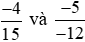 
.
Lời giải:
Ta có: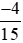 
là phân số âm vì phân số có tử số và mẫu số trái dấu nên 
.
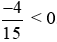Và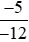 
là phân số dương vì phân số có tử số và mẫu số cùng dấu nên 
.
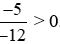Áp dụng tính chất bắc cầu, ta suy ra: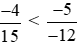 
.
Vậy .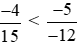
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
