1. Khái niệm hình bình hành
Hình bình hành là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nó là một dạng đặc biệt của hình thang.
Trong không gian 3 chiều, khối tương đương với hình bình hành là hình khối lục diện.
2. Tính chất hình bình hành
Trong hình bình hành:
– Các cạnh đối song song với nhau và bằng nhau.
– Các góc đối bằng nhau.
– Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết hình bình hành
1/ Tứ giác có các cạnh đối song song là hình bình hành.
Tứ giác ABCD có AB//CD và AD//CB thì ABCD là hình bình hành.
2/ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
Tứ giác ABCD có AB = CD, AD =BC thì ABCD là hình bình hành.
3/ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Tứ giác ABCD có AB//CD và AB = CD hoặc AD//BC và AD = BC thì ABCD là hình bình hành.
4/ Tứ giác có các góc đối bằng nhau là hình bình hành.
Tứ giác ABCD có thì ABCD là hình bình hành.
5/ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Tứ giác ABCD có AC cắt BD tại O. Nếu OA = OC, OB = OD thì ABCD là hình bình hành.
4. Diện tích hình bình hành
Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình bình hành.
Diện tích hình bình hành được tính theo công thức bằng tích của cạnh đáy nhân với chiều cao.
SABCD = a.h
Trong đó:
+ S là diện tích hình bình hành
+ a là cạnh đáy của hình bình hành
+ h là chiều cao nối tử đỉnh tới đáy của một hình bình hành.
5. Chu vi hình bình hành
Chu vi hình bình hành được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích, bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ. Nói cách khác, chu vi hình bình hành là tổng độ dài của 4 cạnh.
Công thức cụ thể như sau:
C = 2 x (a+b)
Trong đó:
+ C là chu vi hình bình hành.
+ a và b là cặp cạnh kề nhau của hình bình hành.
6. Ví dụ về hình bình hành
Ví dụ 1: Cho hình bình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB và CD
a. Chứng minh: AF // CE
b. Gọi M, N theo thứ tự là giao điểm của BD với AF, CE. Chứng minh: DM = MN = NB
Hướng dẫn:
%20-%20Google%20Chrome%2019_10_2022%209_06_16%20SA%20(2).png)
a. Vì ABCD là hình bình hành:
⇒ AB = CD (tính chất)
mà E thuộc AB và F thuộc DC ⇒ AE // FC
Vì E, F là trung điểm của AB và CD
⇒ AE = EB = DF = FC
Xét tứ giác AECF có:
AE = FC và AE // FC
⇒ AECF là hình bình hành (DHNB) ⇒ AF // EC (tính chất)
b. Gọi AC giao BD tại O
Xét tam giác ADC có:
DO, AF là trung tuyến (AO = OC, DF = FC)
AF giao DO tại M
⇒ M là trọng tâm của tam giác ADC
⇒ DM = 2/3 DO = 2/3 BO (1)
và OM = 1/3 DO = 1/3 BO (2) (do DO = BO)
Xét tam giác ABC có:
BO, CE là trung tuyến
BO giao CE tại N
⇒ N là trọng tâm của tam giác ABC
⇒ BN = 2/3 BO (3)
và ON = 1/3 BO (4)
Từ (2), (4) ⇒ MN = OM + ON = 1/3 BO + 1/3 BO = 2/3 BO (5)
Từ (1), (3) và (5) ⇒ DM = BN = MN
Ví dụ 2: Hình bình hành ABCD, O là giao điểm của hai đường chéo, E và F theo thứ tự là trung điểm của OD và OB.
a. Chứng minh: AE // CF
b. Gọi AE giao CD tại K. Chứng minh: DK = 1/2 KC
Hướng dẫn:
%20-%20Google%20Chrome%2019_10_2022%209_21_32%20SA%20(2).png)
a. AC giao BD tại O ⇒ OD = BO
Vì E, F là trung điểm của DO và BO ⇒ DE = EO = OF = FB
Xét tứ giác AFCE có:
AC giao EF tại O
OA = OC
OE = OF
⇒ AFCE là hình bình hành (DHNB)
⇒ AE // CF (tính chất)
b. Từ O kẻ OM // EK
Xét tam giác DOM có:
OM // EK
và E là trung điểm của DO
⇒ K là tung điểm của DM ⇒ DK = KM (1)
Xét tam giác CDK có:
OM // AK
và O là trung điểm của AC
⇒ M là trung điểm của KC ⇒ CM = KM (2)
Từ (1) và (2) ⇒ DK = KM = CM
mà KM + CM = KC
⇒ DK = 1/2 KC
Ví dụ 3:
Cho hình bình hành có cạnh đáy bằng 12cm, cạnh bên bằng 7cm, chiều cao bằng 5cm. Hãy tính chu vi và diện tích của hình bình hành đó?
Hướng dẫn:
Chu vi của hình bình hành là:
P = 2( 12 + 7) = 38 (cm)
Diện tích hình bình hành là:
S = a.h = 12.5 = 60 (cm2)
Ví dụ 4: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và ABEˆ = CDFˆ .
Hướng dẫn:
Xét tứ giác BEDF có
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên BADˆ = BCDˆ ( 1 )
BEDF là hình bình hành nên BEDˆ = DFBˆ ( 2 )
Mà
Từ ( 2 ) và ( 3 ) ⇒ AEBˆ = DFCˆ ( 4 )
Xét Δ ABE có BAEˆ + AEBˆ + ABEˆ = 1800 (5)
Xét Δ DFC có DFCˆ + FCDˆ + FDCˆ = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ ABEˆ = CDFˆ (đpcm)
Ví dụ 5: Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.
a) Chứng minh AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Hướng dẫn:
a) Từ giả thiết ta có: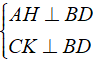
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
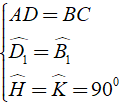
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Ví dụ 6: Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK//CI
b) DM = MN = NB
Hướng dẫn:
a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
b) Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có:
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
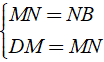
Ví dụ 7: Tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD.
a. Chứng minh: EFGH là hình bình hành
b. Cho AD = a, BC = b. Tính chu vi hình hình hành EFGH
Hướng dẫn:
%20-%20Google%20Chrome%2019_10_2022%209_59_04%20SA%20(2).png)
a. Xét tam giác ABD có:
F và E lần lượt là trung điểm của AB, BD ⇒ EF là đường trung bình của tam giác ABD
⇒ EF // AD (1)
và EF = 1/2 AD (2)
Tương tự, ta có GH là đường trung bình của tam giác ACD
⇒ GH // AD (3)
và GH = 1/2 AD (4)
Từ (1) và (3) ⇒ EF // GH
(2) và (4) ⇒ EF = GH
⇒ tứ giác GHEF là hình bình hành
b. Ta có: GH = EF = 1/2 AD = 1/2 a
FG = HE = 1/2 BC = 1/2 b
Chu vi hình binh hành GFEH là:
C = (1/2 a + 1/2 b) .2 = a + b
Ví dụ 8: Cho tam giác ABH, trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. Chứng minh:
a. BDCH là hình bình hành
b. góc BAC + góc BDC = 180°
c. H, M, D thẳng hàng (M là trung điểm BC)
Hướng dẫn:
%20-%20Google%20Chrome%2019_10_2022%2010_21_41%20SA%20(2).png)
a. Ta có: CH vuông góc AB
và BD vuông góc AB
⇒ CH // DB (1)
Lại có: BH vuông góc AC
và CD vuông góc AC
⇒ BH // CD (2)
Từ (1) và (2) ⇒ BHCD là hình bình hành (DHNB)
b. Tứ giác ABCD có:
góc BAC + góc ABD + góc BDC + góc ACD = 360°
⇒ góc BAC + 90° + góc BDC + 90° = 360°
⇒ góc BAC + góc BDC = 180°
c. Vì BHCD là hình bình hành nên BC cắt HD tại trung điểm của mỗi đường
Ta có: M là tung điểm của BC
⇒ M là trung điểm của HD
⇒ H, M, D thẳng hàng
Ví dụ 9: Hình bình hành ABCD. Lấy N thuộc AB, M thuộc CD sao cho AN = CM. Chứng minh:
a. AM // CN
b. DN = BM
c. AC, BD, MN đồng quy
Hướng dẫn:
%20-%20Google%20Chrome%2019_10_2022%2010_31_32%20SA%20(2).png)
a. Xét tứ giác ABCD có:
AN = CM
AN // CM (do AB//CD)
⇒ ANCM là hình bình hành
⇒ AM // CN
b. Ta có: BN = AB - AN
DM = DC - CM
mà AB = DC, AN = CM
⇒ BN = DM
mà BN // DM (do AB // CD)
⇒ BNDM là hình bình hành (DHNB)
⇒ DN = BM (tính chất)
c. Gọi AC giao BD tại O (1)
⇒ O là trung điểm của AC và BD
Ta có: ANCM là hình bình hành và O là trung điểm cua đường chéo Ac
⇒ O là trung điểm của MN
⇒ O thuộc MN (2)
Từ (1) và (2) ⇒ AC, BD, MN đồng quy
Ví dụ 10: Một mảnh đất hình bình hành có cạnh đáy là 47m, mở rộng mảnh dất bằng cách tăng cạnh đáy của hình bình hanh thêm 7m, thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là 189 m2. Tính diện tích mảnh đất ban đầu?
Hướng dẫn:
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy 7m và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: 189 ; 7 = 27m
Diện tích mảnh đất hình bình hành ban đầu là: S = 27 . 47 = 1269 m2