Với giải Bài 6.22 trang 27 SGK Toán 10 Kết nối tri thức chi tiết trong Bài 18: Phương trình quy về phương trình bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 18: Phương trình quy về phương trình bậc hai
Bài 6.22 trang 27 Toán 10 Tập 2: Cho tứ giác ABCD có AB ⊥ CD; AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21). Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
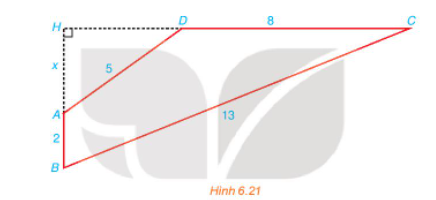
Lời giải:
Đặt AH = x, x > 0.
Khi đó theo định lí Pythagore trong tam giác AHD vuông tại H, ta có:
AD2= AH2 + HD2 ⇔ HD2 = AD2 – AH2 = 52 – x2 = 25 – x2.
Suy ra HD = .
Ta lại có HC = HD + DC = .
HB = AH + AB = x + 2
Theo định lí Pythagore trong tam giác HBC vuông tại H, ta có: BC2 = HB2 + HC2
⇔ 132 = (x + 2)2 +
⇔ x2 + 4x + 4 + 25 – x2 + 16+ 64 – 169 = 0
⇔ 16 = – 4x + 76
⇔ 4 = 19 – x
Để tính x, ta cần giải phương trình: 4 = 19 – x (*).
Bình phương hai vế của phương trình (*) ta được:
16.(25 – x2) = x2 – 38x + 361
⇔ 17x2 – 38x – 39 = 0
⇔ x = 3 hoặc x = .
Thay lần lượt các giá trị trên vào phương trình (*), ta thấy hai giá trị x = 3 và x = đều thỏa mãn.
Vì điều kiện của x là x > 0 nên ta chọn x = 3.
Vậy ta tính được AH = 3.
Suy ra HD = ; HC = 4 + 8 = 12; HB = 3 + 2 = 5
Diện tích tam giác HAD là SHAD = HA . HD = . 3 . 4 = 6.
Diện tích tam giác HBC là SHBC = HB . HC = . 5 . 12 = 30.
Vậy diện tích tứ giác ABCD là S = SHBC – SHAD = 30 – 6 = 24 (đvdt).
Xem thêm lời giải sách giáo khoa Toán 10 Kết nối tri thức hay, chi tiết khác:
Hoạt động 1 trang 25 Toán 10 Tập 2: Cho phương trình...
Luyện tập 1 trang 25 Toán 10 Tập 2: Giải các phương trình sau:...
Hoạt động 2 trang 25 Toán 10 Tập 2: Cho phương trình...
Luyện tập 2 trang 26 Toán 10 Tập 2: Giải các phương trình sau:...
Bài 6.20 trang 27 Toán 10 Tập 2: Giải các phương trình sau:...
Bài 6.21 trang 27 Toán 10 Tập 2: Giải các phương trình sau:...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 17: Dấu của tam thức bậc hai
Bài 18: Phương trình quy về phương trình bậc hai
Bài 19: Phương trình đường thẳng
Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
