Với Giải toán lớp 7 trang 79 Tập 2 Cánh diều tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 79 Tập 2 Cánh diều

Hoạt động 2 trang 79 Toán 7 Tập 2: Quan sát hai tam giác ABC và A'B'C' trên một tờ giấy kẻ ô vuông (Hình 30).

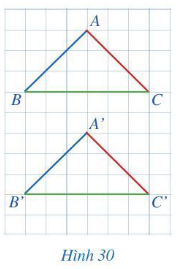
a) So sánh:

– Các cặp cạnh: AB và A'B'; BC và B'C'; CA và C'A'.

– Các cặp góc: $\widehat{A}$ và $\widehat{A^{\text{'}}}$; $\widehat{B}$ và $\widehat{B^{\text{'}}}$, $\widehat{C}$ và $\widehat{C^{\text{'}}}.$  

b) Hai tam giác ABC và A'B'C' có bằng nhau hay không?

c) Cắt mảnh giấy hình tam giác ABC và mảnh giấy hình tam giác A'B'C', hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?

Lời giải:

Ta coi cạnh của hình ô vuông nhỏ là 1 đơn vị.

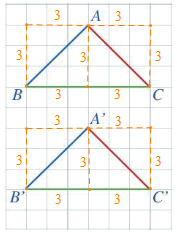
Khi đó cạnh AB là đường chéo của hình vuông có cạnh bằng 3 đơn vị;

Tương tự:

+ Cạnh A'B' là đường chéo của hình vuông có cạnh bằng 3 đơn vị;

+ Cạnh AC là đường chéo của hình vuông có cạnh bằng 3 đơn vị;

+ Cạnh A'C' là đường chéo của hình vuông có cạnh bằng 3 đơn vị;

+ Cạnh BC có độ dài bằng 6 đơn vị;

+ Cạnh B'C' có độ dài bànge 6 đơn vị.

a) Do đó ta có: AB = A'B'; BC = B'C'; CA = C'A';

Sử dụng thước đo góc ta đo được $\widehat{A}=\widehat{A^{\text{'}}}=90°;$ $\widehat{B}=\widehat{B^{\text{'}}}=45°;$ $\widehat{C}=\widehat{C^{\text{'}}}=45°.$  

b) Xét tam giác ABC và tam giác A'B'C' ta có:

+) AB = A'B'; BC = B'C'; CA = C'A';

+) $\widehat{A}=\widehat{A^{\text{'}}};$ $\widehat{B}=\widehat{B^{\text{'}}};$ $\widehat{C}=\widehat{C^{\text{'}}}.$  

Do đó ∆ABC = ∆A'B'C'.

c) Ta có thể đặt mảnh giấy hình tam giác ABC chồng khít lên mảnh giấy hình tam giác A'B'C'.

Luyện tập trang 79 Toán 7 Tập 2: Cho biết ∆ABC = ∆MNP, AC = 4 cm, $\widehat{MPN}=45°.$ Tính độ dài cạnh MP và số đo góc ACB.

Lời giải:

Vì ∆ABC = ∆MNP (giả thiết) nên ta có:

+) AC = MP (hai cạnh tương ứng) mà AC = 4 cm nên MP = 4 cm;

 +) $\widehat{ABC}=\widehat{MPN}$ (hai góc tương ứng) mà $\widehat{MPN}=45°$ nên $\widehat{ABC}=45°.$

Vậy MP = 4 cm và $\widehat{ABC}=45°.$

B. Bài tập

Bài 1 trang 79 Toán 7 Tập 2: Cho biết ∆ABC = ∆DEG, AB = 3 cm, BC = 4 cm, CA = 6 cm. Tìm độ dài các cạnh của tam giác DEG.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

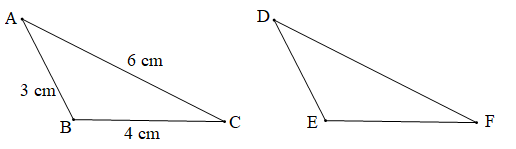
Vì ∆ABC = ∆DEG (giả thiết) nên ta có:

AB = DE; BC = EG; CA = GD (các cặp cạnh tương ứng)

Mà AB = 3 cm, BC = 4 cm, CA = 6 cm

Nên DE = 3 cm, EG = 4 cm, GD = 6 cm.

Vậy độ dài ba cạnh của tam giác DEG là: DE = 3 cm, EG = 4 cm, GD = 6 cm.

Bài 2 trang 79 Toán 7 Tập 2: Cho biết ∆PQR = ∆IHK, $\widehat{P}=71°,\widehat{Q}=49°.$ Tính số đo góc K của tam giác IHK.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

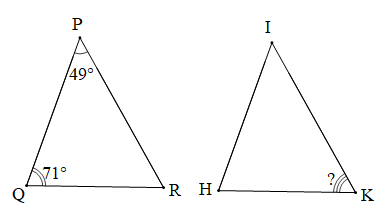
Xét tam giác PQR có: $\widehat{P}+\widehat{Q}+\widehat{R}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{R}=180°-\widehat{P}-\widehat{Q}$ 

Mà $\widehat{P}=71°,\widehat{Q}=49°$(giả thiết)

Do đó $\widehat{R}=180°-71°-49°=60°.$

Vì ∆PQR = ∆IHK (giả thiết) nên ta có: $\widehat{R}=\widehat{K}$ (hai góc tương ứng)

Mà $\widehat{R}=60°.$

Do đó $\widehat{K}=60°.$

Vậy số đo góc K của tam giác IHK bằng 60°.

Bài 3 trang 79 Toán 7 Tập 2: Cho ∆ABC = ∆MNP và $\widehat{A}+\widehat{N}=125°.$ Tính số đo góc P.

Lời giải:

Chứng minh (Hình vẽ dưới đây)

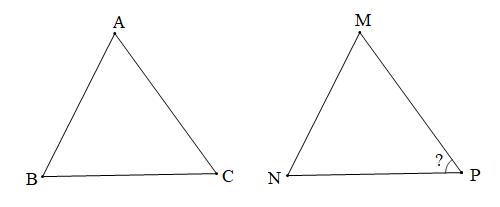
Vì ∆ABC = ∆MNP (giả thiết) nên ta có: $\widehat{A}=\widehat{M},\widehat{B}=\widehat{P},\widehat{C}=\widehat{N}$ (các cặp góc tương ứng)

Mà $\widehat{A}+\widehat{N}=125°$ (giả thiết)

Suy ra $\widehat{M}+\widehat{N}=125°.$

Xét tam giác MNP có: $\widehat{M}+\widehat{N}+\widehat{P}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{P}=180°-\left(\widehat{M}+\widehat{N}\right)$

Hay $\widehat{P}=180°-125°=55°$

Vậy số đo góc P của tam giác MNP bằng 55°.

Bài 4 trang 79 Toán 7 Tập 2: Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 32).

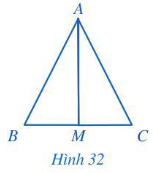
Chứng minh rằng:

a) M là trung điểm của đoạn thẳng BC;

b) Tia AM là tia phân giác của góc BAC và $AM\perp BC.$  

Lời giải:

Chứng minh (Hình 32):

a) Vì ∆AMB = ∆AMC (giả thiết) nên ta có: MB = MC (hai cạnh tương ứng)

Suy ra M là trung điểm của BC.

b) Vì ∆AMB = ∆AMC (giả thiết) nên ta có:

+) $\widehat{BAM}=\widehat{CAM}$ (hai góc tương ứng) do đó tia AM là tia phân giác của góc BAC;

+) $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng)

Lại có $\widehat{AMB}$ và $\widehat{AMC}$ là hai góc kề bù nên: $\widehat{AMB}+\widehat{AMC}=180°$ (tính chất hai góc kề bù)

Suy ra $\widehat{AMB}+\widehat{AMB}=180°$

Hay $2.\widehat{AMB}=180°$

Do đó $\widehat{AMB}=180°:2=90°$

Suy ra $AM\perp BC.$ 

Vậy tia AM là tia phân giác của góc BAC và $AM\perp BC.$

Xem thêm các bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Giải Toán 7 trang 78 Tập 2