Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Hệ hai phương trình bậc nhất hai ẩn
a)
b)
c)
d)
Phương pháp giải:
Sử dụng:
Ta thay giá trị và vào từng phương trình của hệ. Nếu cặp số thỏa mãn cả hai phương trình của hệ thì cặp số đó là một nghiệm của hệ phương trình đã cho.
Lời giải:
a)
Thay vào từng phương trình của hệ:
+) (luôn đúng)
+) (luôn đúng)
Vậy cặp là nghiệm của hệ phương trình
b)
Thay vào từng phương trình của hệ:
+)(luôn đúng)
+) (luôn đúng)
Vậy cặp là nghiệm của hệ phương trình
c)
Thay vào từng phương trình của hệ:
+) (luôn đúng)
+)(luôn đúng)
Vậy cặp là nghiệm của hệ phương trình
Thay vào từng phương trình của hệ:
(luôn đúng)
(luôn đúng)
Vậy cặp là nghiệm của hệ phương trình
d)
Thay vào phương trình thứ nhất của hệ:
(vô lí)
Vậy cặp không phải là nghiệm của hệ phương trình
a)
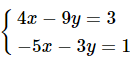
b)
c)
d)
Phương pháp giải:
Sử dụng:
- Ta biến đổi các hệ phương trình đã cho về dạng
- Với hai đường thẳng và trong đó và khác . Ta so sánh các hệ số ; .
+) Nếu thì cắt hệ đã cho có một nghiệm duy nhất.
+) Nếu thì song song với hệ đã cho vô nghiệm.
+) Nếu thì trùng với hệ đã cho có vô số nghiệm.
Lời giải:
a)
Ta có , nên .
Do đó , cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
b)
Đường thẳng cắt hai trục tọa độ, đường thẳng song song với trục hoành nên hai đường thẳng trên cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
c)
Đường thẳng song song với trục tung, đường thẳng cắt hai trục tọa độ nên hai đường thẳng đó cắt nhau.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
d)
Ta có và nên .
Do đó , song song với nhau.
Vậy hệ phương trình đã cho vô nghiệm.
a) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất
b) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ vô nghiệm
c) Hãy cho thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm
Phương pháp giải:
Sử dụng:
- Với hai đường thẳng và trong đó và khác . Ta so sánh các hệ số ; .
+) Nếu thì cắt hệ đã cho có một nghiệm duy nhất.
+) Nếu thì song song với hệ đã cho vô nghiệm.
+) Nếu thì trùng với hệ đã cho có vô số nghiệm.
Lời giải:
a)
Ta có
Ta cần thêm một phương trình bậc nhất hai ẩn để được một hệ có nghiệm duy nhất. Do đó ta phải thêm đường thẳng có hệ số góc khác .
Chẳng hạn ta thêm đường thẳng
Khi đó ta có hệ phương trình
và hệ này có nghiệm duy nhất.
b)
Ta cần thêm một phương trình bậc nhất hai ẩn để được môt hệ vô nghiệm. Do đó ta phải thêm đường thẳng có hệ số góc bằng và tung độ gốc khác .
Chẳng hạn ta thêm đường thẳng
Khi đó ta có hệ phương trình
và hệ này vô nghiệm.
c)
Ta cần thêm một phương trình bậc nhất hai ẩn để được một hệ có vô số nghiệm. Do đó ta phải thêm đường thẳng có hệ số góc bằng và tung độ gốc bằng
Chẳng hạn ta thêm đường thẳng
Khi đó ta có hệ phương trình
và hệ này có vô số nghiệm.
Có nghiệm duy nhất
Vô nghiệm
Có vô số nghiệm
Áp dụng:
Hãy lập một hệ hai phương trình bậc nhất hai ẩn có nghiệm duy nhất
Hãy lập một hệ hai phương trình bậc nhất hai ẩn vô nghiệm
Hãy lập một hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm
Phương pháp giải:
Sử dụng:
- Với hai đường thẳng và trong đó và khác . Ta so sánh các hệ số ; .
+) Nếu thì cắt hệ đã cho có một nghiệm duy nhất.
+) Nếu thì song song với hệ đã cho vô nghiệm.
+) Nếu thì trùng với hệ đã cho có vô số nghiệm.
Lời giải:
Ta chia ra các trường hợp:
Trường hợp đều khác
Hệ phương trình đã cho có nghiệm duy nhất khi hai đường thẳng và cắt nhau tức là hai đường thẳng này có hệ số góc khác nhau. Do đó hay
Hệ phương trình đã cho vô nghiệm khi hai đường thẳng và song song. Tức là hai đường thẳng này có hệ số góc bằng nhau và tung độ gốc khác nhau. Do đó:
hay (nếu ) hoặc (nếu )
Hệ phương trình đã cho có vô số nghiệm khi hai đường thẳng và trùng nhau tức là hai đường thẳng này có cùng hệ số góc và tung độ gốc. Do đó
hay (nếu ) hoặc (nếu )
Trường hợp và
Hoặc
Vì đường thẳng song song hoặc trùng với trục , còn đường thẳng và đường thẳng luôn luôn cắt trục hoành nên đường thẳng luôn luôn cắt hai đường thẳng và . Do đó hệ phương trình đã cho có nghiệm duy nhất.
Tương tự trường hợp và , hệ phương trình đã cho cũng có nghiệm duy nhất.
Trường hợp
Hệ đã cho vô nghiệm khi
Hệ đã cho có vô số nghiệm khi
Trường hợp
Vì đường thẳng song song hoặc trùng với trục , còn đường thẳng luôn cắt trục nên hai đường thẳng này luôn luôn cắt nhau. Do đó hệ đã cho có nghiệm duy nhất.
Tương tự trường hợp và , hệ phương trình đã cho cũng có nghiệm duy nhất.
Trường hợp
Hệ vô nghiệm khi hai đường thẳng đó song song:
Hệ có vô số nghiệm khi hai đường thẳng đó trùng nhau:
Áp dụng
Hệ phương trình có một nghiệm duy nhất vì
Hệ phương trình
vô nghiệm vì
Hệ phương trình có vô số nghiệm vì
a)
b)
c)
d)
Phương pháp giải:
Sử dụng:
- Ta biến đổi hệ phương trình đã cho về dạng
+) Vẽ hai đường thẳng và trong cùng một hệ trục tọa độ.
+) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ.
+) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
Lời giải:
a)
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm
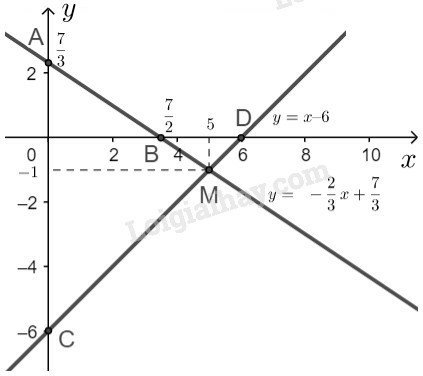
- Quan sát hình vẽ, ta thấy hai đường thẳng và cắt nhau tại điểm
Thay vào hệ phương trình đã cho ta được:
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
b)
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm
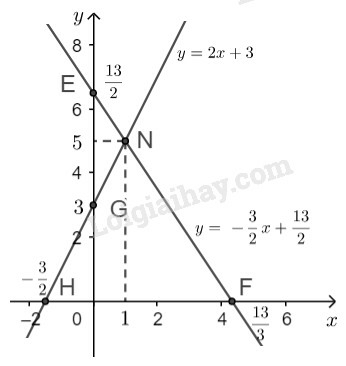
- Quan sát hình vẽ, ta thấy hai đường thẳng và cắt nhau tại điểm
Thay vào hệ phương trình đã cho ta được:
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
c)
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Vẽ đường thẳng :
Đường thẳng đi qua điểm và song song với trục tung.
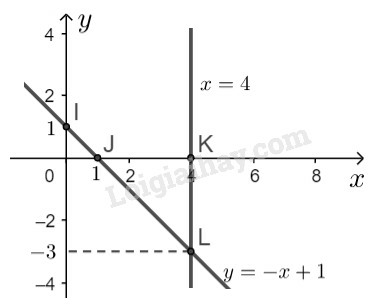
- Quan sát hình vẽ, ta thấy hai đường thẳng và cắt nhau tại điểm
Thay vào hệ phương trình đã cho ta được:
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
d)
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Vẽ đường thẳng :
Đường thẳng đi qua điểm và song song với trục hoành.
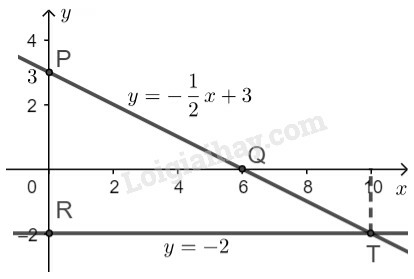
- Quan sát hình vẽ, ta thấy hai đường thẳng và cắt nhau tại điểm
Thay vào hệ phương trình đã cho ta được:
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
a) Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
b) Nghiệm của hệ này có phải là nghiệm của phương trình hay không?
Phương pháp giải:
Sử dụng:
- Ta biến đổi hệ phương trình đã cho về dạng
+) Vẽ hai đường thẳng và trong cùng một hệ trục tọa độ.
+) Xác định giao điểm của hai đường thẳng đã cho dựa vào hình vẽ.
+) Thử lại tọa độ giao điểm đó vào hệ phương trình ban đầu. Nếu thỏa mãn thì là nghiệm của hệ.
- Một cặp số là một nghiệm của phương trình ( hoặc ) khi và chỉ khi
Lời giải:
a)
- Vẽ đường thẳng :
Đường thẳng là đường thẳng đi qua điểm và song song với trục tung.
- Vẽ đường thẳng :
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm
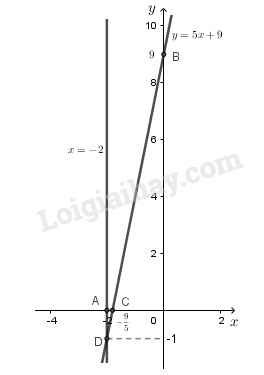
- Quan sát hình vẽ, ta thấy hai đường thẳng và cắt nhau tại điểm
Thay vào hệ phương trình đã cho ta được:
Vậy hệ phương trình đã cho có nghiệm duy nhất là .
b)
Thay vào phương trình ta có:
(luôn đúng)
Vậy cặp là nghiệm của phương trình
Hỏi đường thẳng có đi qua giao điểm của và hay không?
Phương pháp giải:
Sử dụng:
- Vẽ đường thẳng có phương trình :
Ta có .
+) Cho ta được
+) Cho ta được
Đường thẳng đã cho là đường thẳng đi qua hai điểm .
- Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình: .
Giải phương trình trên ta tìm được . Thay giá trị của vào phương trình hoặc , ta tìm được tung độ giao điểm.
- Đường thẳng đi qua điểm .
Lời giải:
- Vẽ đường thẳng
Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Vẽ đường thẳng
Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
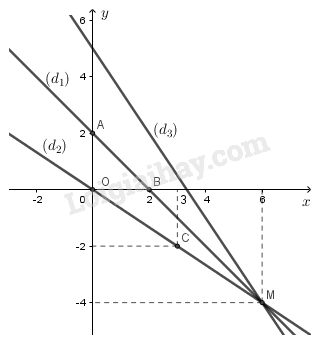
- Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình:
Suy ra tung độ giao điểm là
Vậy tọa độ giao điểm của hai đường thẳng và là
Thay vào phương trình đường thẳng ta được:
Vậy đường thẳng đi qua giao điểm của và .
Phương pháp giải:
Sử dụng:
- Tìm giao điểm của hai đường thẳng bất kì:
Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình: .
Giải phương trình trên ta tìm được . Thay giá trị của vào phương trình hoặc , ta tìm được tung độ giao điểm.
- Nếu hai đường thẳng còn lại cùng đi qua điểm thì 4 đường thẳng đã cho đồng quy tại điểm .
- Đường thẳng đi qua điểm .
Lời giải:
- Ta có
Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình:
Suy ra tung độ giao điểm là
Vậy tọa độ giao điểm của hai đường thẳng và là
- Nếu cùng đi qua điểm thì bốn đường thẳng đã cho đồng quy.
Thay vào phương trình đường thẳng ta được:
(luôn đúng)
Do đó đi qua .
Thay vào phương trình đường thẳng ta được:
(luôn đúng)
Do đó đi qua .)
Vậy bốn đường thẳng đã cho đồng quy tại
Bài tập bổ sung (trang 8 SBT Toán 9)
Phương pháp giải:
Sử dụng:
- Cho hệ hai phương trình bậc nhất hai ẩn:
+ Nếu cắt thì hệ có một nghiệm duy nhất.
+ Nếu song song với thì hệ vô nghiệm.
+ Nếu trùng với thì hệ có vô số nghiệm.
Lời giải:
Đường thẳng song song với trục tung, đường thẳng cắt trục tung nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
Đường thẳng song song với trục hoành, đường thẳng cắt trục hoành nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
Đường thẳng song song với trục tung, đường thẳng cắt trục tung nên hai đường thẳng trên cắt nhau. Vậy hệ phương trình đã cho có nghiệm duy nhất.
Phương pháp giải:
Sử dụng:
- Cho hệ hai phương trình bậc nhất hai ẩn:
+ Nếu cắt thì hệ có một nghiệm duy nhất.
+ Nếu song song với thì hệ vô nghiệm.
+ Nếu trùng với thì hệ có vô số nghiệm.
Lời giải:
Đường thẳng song song với trục tung, đường thẳng cũng song song với trục tung nên chúng song song với nhau (vì
Vậy hệ phương trình đã cho vô nghiệm.
Ta có ;
Do đó đường thẳng và đường thẳng trùng nhau.
Vậy hệ phương trình đã cho có vô số nghiệm.
Ta có ;
Do đó đường thẳng và đường thẳng trùng nhau. Vậy hệ phương trình đã cho có vô số nghiệm.
Đường thẳng và đường thẳng đều song song với trục hoành nên chúng song song với nhau. Vậy hệ phương trình đã cho vô nghiệm.