Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 2: Hệ hai phương trình bậc nhất hai ẩn . Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 2: Hệ hai phương trình bậc nhất hai ẩn . Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 2: Hệ hai phương trình bậc nhất hai ẩn
A. Bài tập Hệ hai phương trình bậc nhất hai ẩn
I. Bài tập trắc nghiệm
Câu 1: Hệ phương trình 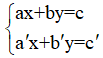
Chọn đáp án A
Câu 2: Hệ hai phương trình bậc nhất hai ẩn 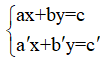
Chọn đáp án B
Câu 3: Hệ hai phương trình 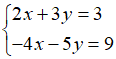
A. (-21; 15)
B. (21; -15)
C. (1; 1)
D. (1; -1)
Thay lần lượt các cặp số (21; -15); (1; 1); (1; -1); (-21; 15) vào hệ phương trình ta được
Chọn đáp án A
Câu 4: Cặp số (-2; -3) là nghiệm của hệ phương trình nào sau đây ?
Chọn đáp án C
Câu 5: Không giải hệ phương trình, dự đoán số nghiệm của hệ
A. 0
B. Vô số
C. 1
D. 2
Tập nghiệm phương trình -2x + y = -3 được biểu diễn bởi đường thẳng -2x + y = -3
Tập nghiệm phương trình 3x – 2y = 7 được biểu diễn bởi đường thẳng 3x – 2y = 7
Ta có 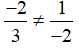
Chọn đáp án C
Câu 6: Không cần vẽ hình, cho biết mỗi hệ phương trình sau có bao nhiêu nghiệm?
A. 1
B. Vô số
C. 0
D. 2
+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d1:y = 2x + 10.
+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d2: y = x + 100.
Lại có: hệ số góc của hai đường thẳng d1; d2 khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.
Suy ra, hệ phương trình đã cho có nghiệm duy nhất.
Chọn đáp án A.
Câu 7: Không vẽ hình, hãy cho biết hệ phương trình sau có bao nhiêu nghiệm?
A. 1
B. Vô số
C. 0
D. 2
Lời giải:
Ta có:
Nên tập nghiệm của phương trình x – 2y + 10 = 0 được biểu diễn bởi đường thẳng (d1):
Nên tập nghiệm của phương trình -3x +6y – 30= 0 được biểu diễn bởi đường thẳng (d2):
Do đó, nên hệ phương trình đã cho có vô số nghiệm.
Chọn đáp án B.
Câu 8: Không vẽ hình, hỏi hệ phương trình sau có bao nhiêu nghiệm:
A. Vô số nghiệm
B. 0
C.1
D. 2
Ta có:
Nên tập nghiệm của phương trình – 2x + 5y = 10 được biểu diễn bởi đường thẳng (d1):
Nên tập nghiệm của phương trình 16x – 40y = 20 được biểu diễn bởi đường thẳng (d2):
Hai đường thẳng d1; d2 có cùng hệ số góc và có tung độ góc khác nhau nên d1// d2.
Suy ra, hệ phương trình đã cho vô nghiệm.
Chọn đáp án B.
Câu 9: Cho hệ phương trình 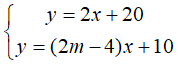
A. m = 3
B. m = 1
C. m = -2
D. m = -1
Nghiệm phương trình y = 2x + 20 được biểu diễn bởi đường thẳng (d1): y =2x +20.
Nghiệm phương trình y = (2m - 4)x + 10 được biểu diễn bởi đường thẳng (d2): y = (2m – 4)x + 10.
Để hệ phương trình đã cho vô nghiệm khi 2 đường thẳng d1 // d2
Chọn đáp án A.
Câu 10: Cho hệ phương trình 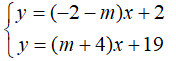
A. m = 3
B. m = -3
C. m ≠ -3
D. m ≠ 3
Nghiệm phương trình y = (-2 - m)x + 2 được biểu diễn bởi đường thẳng (d1): y =(-2 - m)x + 2
Nghiệm phương trình y = (m + 4)x + 19 được biểu diễn bởi đường thẳng (d2): y = (m +4)x +19
Để hệ phương trình đã cho có nghiệm duy nhất khi và chỉ khi hai đường thẳng cắt nhau nên:
-2 - m ≠ m + 4 ⇔ -2m ≠ 6 ⇔ m ≠ -3
Chọn đáp án D.
Câu 11: Xác định giá trị của tham số m để hệ phương trình 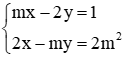
A. m ≠ 2
B. m ≠ −2
C. m = 2
D. m ≠ ± 2
Để hệ phương trình 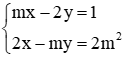
Đáp án cần chọn là: D
Câu 12: Xác định giá trị của tham số m để hệ phương trình 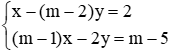
A. m ≠ 0
B. m ≠ 2
C. m ≠ {0;3}
D. m = 0; m = 3
Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng 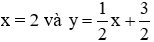
Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng:
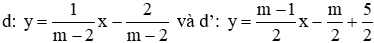
Suy ra m ≠ {0; 2; 3}
Kết hợp cả TH1 và TH2 ta có m ≠ {0; 3}
Vậy hệ phương trình đã cho có nghiệm duy nhất khi m ≠ {0; 3}
Đáp án cần chọn là: C
Câu 13: Hệ phương trình 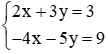
A. (−21; 15)
B. (21; −15)
C. (1; 1)
D. (1; −1)
Thay lần lượt các cặp số (−21; 15); (21; −15); (1; 1) và (1; −1) vào hệ phương trình ta được:
+) Với cặp số (21; −15) thì ta có 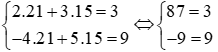
+) Với cặp số (1; 1) thì ta có 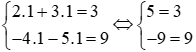
+) Với cặp số (1; −1) thì ta có 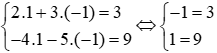
+) Với cặp số (−21; 15) thì ta có 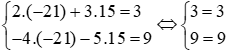
Đáp án cần chọn là: A
Câu 14: Hệ phương trình 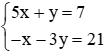
A. (1; 2)
B. (8; −3)
C. (3; −8)
D. (3; 8)
+) Với cặp số (1; 2) thì ta có 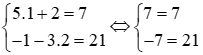
+) Với cặp số (8; −3) thì ta có 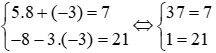
+) Với cặp số (3; 8) thì ta có 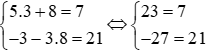
+) Với cặp số (3; −8) thì ta có 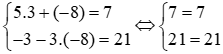
Đáp án cần chọn là: C
Câu 15: Cho hệ phương trình 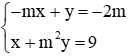
A. m = 0
B. m = −1
C. m = −2
D. m = 3
Để hệ phương trình 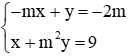
Vậy m = −2
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
Câu 1: Cho hai hệ phương trình 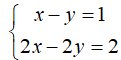
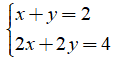
Lời giải:
Xét hệ 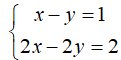
Nhưng với cặp nghiệm (1; 0) lại không phải là nghiệm của hệ 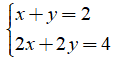
Khi đó hai hệ này không tương đương với nhau (dù cả hai hệ đều có vô số nghiệm)
III. Bài tập vận dụng
Câu 1: Tìm giá trị a để hai hệ phương trình sau tương đương 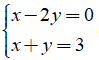
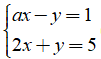
Câu 2: Bằng phương pháp thế hãy giải các hệ phương trình sau:
a)
b)
c)
d)
Câu 3: Bằng phương pháp cộng đại số giải các hệ phương trình sau.
a)
b)
c)
d)
Câu 4: Giải các hệ phương trình sau:
a)
b)
c)
d)
e)
f)
g)
B. Lý thuyết Hệ hai phương trình bậc nhất hai ẩn
1. Khái niệm về hệ hai phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b'y = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
Ví dụ 1:
; là các hệ hai phương trình bậc nhất hai ẩn.
+ Nếu hai phương trình có nghiệm chung là (x0; y0) thì (x0; y0) được gọi là một nghiệm của hệ phương trình (I).
+ Nếu hai phương trình không có nghiệm chung thì hệ phương trình (I) vô nghiệm.
+ Giải hệ phương trình là tìm tất cả các nghiệm của nó.
2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
Cho hai phương trình bậc nhất hai ẩn là ax + by = c và a'x + b'y = c'. Khi đó ta có hệ phương trình bậc nhất hai ẩn là:
Gọi (d) và (d') là đồ thị hàm số của 2 hàm số rút ra từ 2 phương trình bậc nhất hai ẩn của (I).
Đối với hệ phương trình (I), ta có:
Nếu (d) cắt (d') thì hệ (I) có một nghiệm duy nhất.
Nếu (d) song song với (d') thì hệ (I) vô nghiệm.
Nếu (d) trùng với (d') thì hệ (I) có vô số nghiệm.
Ví dụ 2: Xét hệ phương trình
Ta có: x – y = 0 (d)
x + y = 0 (d’)
Vẽ hai đường thẳng (d) và (d’) lên hệ trục tọa độ ta được:
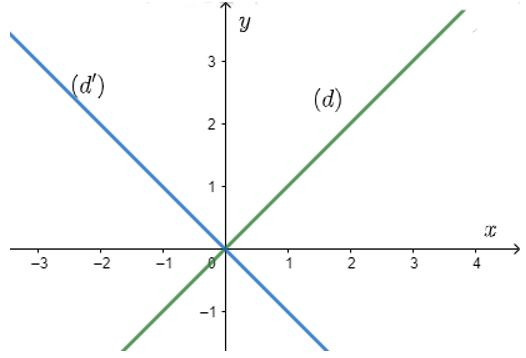
Ta thấy (d) và (d’) cắt nhau tại O(0; 0) nên (0; 0) là nghiệm của hệ phương trình.
Chú ý: Với trường hợp
Hệ phương trình có nghiệm duy nhất ;
Hệ phương trình vô nghiệm ;
Hệ phương trình vô số nghiệm .
3. Hệ phương trình tương đương
Định nghĩa: Hệ hai phương trình được gọi là tương đương với nhau nếu chúng có cùng một tập nghiệm.
Ta cũng dùng kí hiệu “” để chỉ sự tương đương của hai phương trình.






