Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 1: Phương trình bậc nhất hai ẩn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 1: Phương trình bậc nhất hai ẩn
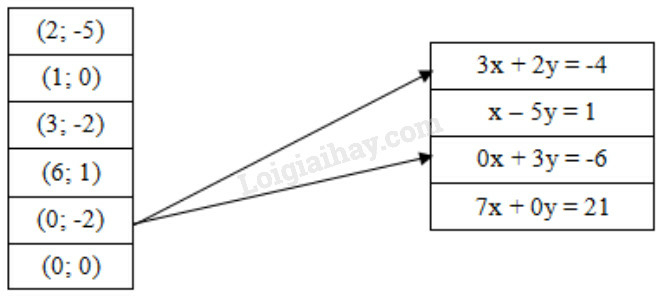
Phương pháp giải:
Sử dụng:
- Một nghiệm của phương trình ( hoặc ) là một cặp số sao
cho
Lời giải:
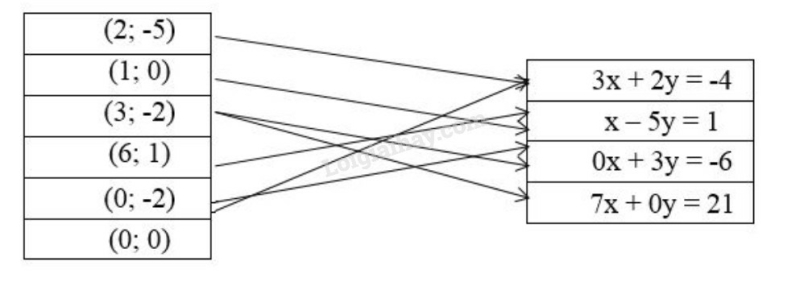
Xét cặp số
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được: (vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
Xét cặp số
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
Xét cặp số
- Thay vào phương trình ta được: (vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
Xét cặp số
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
Xét cặp số
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(luôn đúng)
Do đó cặp số là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
Xét cặp số
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
- Thay vào phương trình ta được:
(vô lí)
Do đó cặp số không phải là nghiệm của phương trình .
Phương pháp giải:
Sử dụng:
Tìm nghiệm tổng quát của phương trình
+) Nếu và thì phương trình có nghiệm tổng quát là:
hoặc
+) Nếu thì phương trình có nghiệm tổng quát là:
+) Nếu thì phương trình có nghiệm tổng quát là:
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng . Cách vẽ đường thẳng có phương trình:
+) Nếu thì vẽ đường thẳng
+) Nếu thì vẽ đường thẳng song song hoặc trùng với trục tung.
+) Nếu thì vẽ đường thẳng song song hoặc trùng với trục hoành.
Lời giải:
Ta có
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Cho ta được .
Cho ta được .
Biểu diễn điểm và trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm .
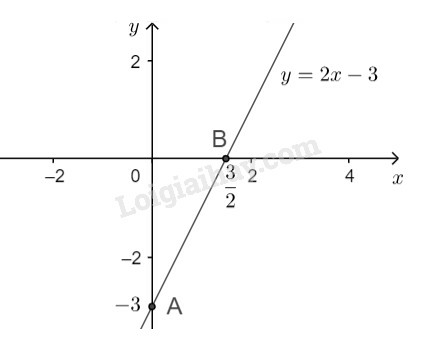
Ta có
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Cho ta được .
Cho ta được .
Biểu diễn điểm và trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm .
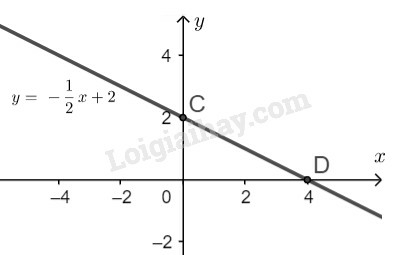
Ta có
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Cho ta được .
Cho ta được .
Biểu diễn điểm và trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm .
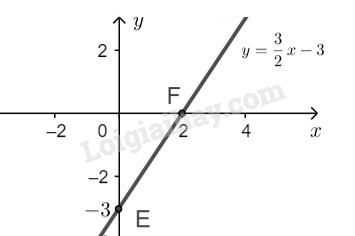
Ta có
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Cho ta được .
Cho ta được .
Biểu diễn điểm và trên hệ trục tọa độ. Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua hai điểm .
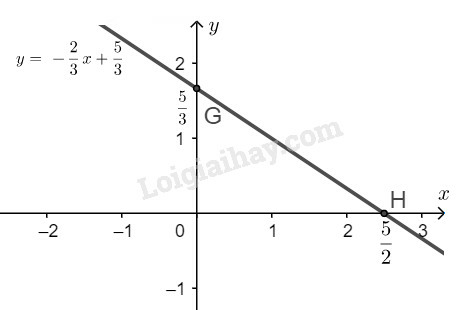
Ta có
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua điểm và song song với trục hoành
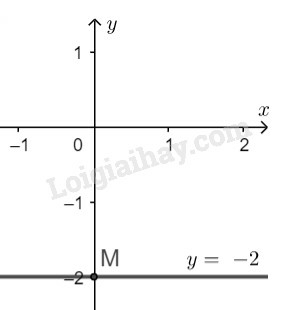
Nghiệm tổng quát của phương trình đã cho là:
* Vẽ đường thẳng biểu diễn tập nghiệm của phương trình :
Tập nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng đi qua điểm và song song với trục tung.
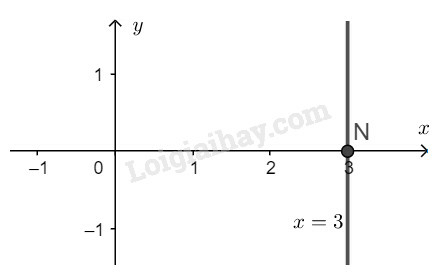
a) Điểm thuộc đường thẳng
b) Điểm thuộc đường thẳng
c) Điểm thuộc đường thẳng
d) Điểm thuộc đường thẳng .
e) Điểm thuộc đường thẳng
f) Điểm thuộc đường thẳng
g) Điểm thuộc đường thẳng
Phương pháp giải:
Sử dụng:
- Điểm thuộc đường thẳng
Lời giải:
a)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm
b)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua
c)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm
d)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm
e)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm
f)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm
g)
Điểm thuộc đường thẳng nên ta có:
Vậy với thì đường thẳng đi qua điểm .
a)
b)
c)
d)
Phương pháp giải:
Sử dụng:
- Biến đổi phương trình đã cho về dạng . Sau đó xác định .
Lời giải:
a)
.
Phương trình trên xác định một hàm số dạng với ;
b)
.
Phương trình trên xác định một hàm số dạng với
c)
.
Phương trình trên xác định một hàm số dạng với
d)
.
Phương trình trên không xác định hàm số dạng
Sử dụng:
- Biến đổi phương trình về dạng một hàm số bậc nhất của biến từ đó suy ra điều kiện của .
Lời giải:
Ta có:
Để phương trình xác định một hàm số bậc nhất của biến có dạng: thì và .
a) và
b) và
c) và
d) và
Phương pháp giải:
Sử dụng:
1) Vẽ đường thẳng có phương trình :
Ta có .
Xác định hai điểm thuộc đồ thị hàm số .
Đường thẳng đã cho là đường thẳng đi qua hai điểm .
2) Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình: .
Giải phương trình trên ta tìm được . Thay giá trị của vào phương trình hoặc , ta tìm được tung độ giao điểm.
Lời giải:
a)
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
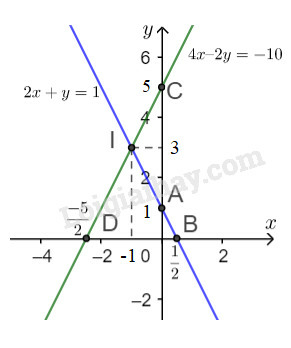
- Tìm tọa độ giao điểm:
Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình:
Suy ra tung độ giao điểm là
Vậy tọa độ giao điểm của hai đường thẳng đã cho là
b)
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
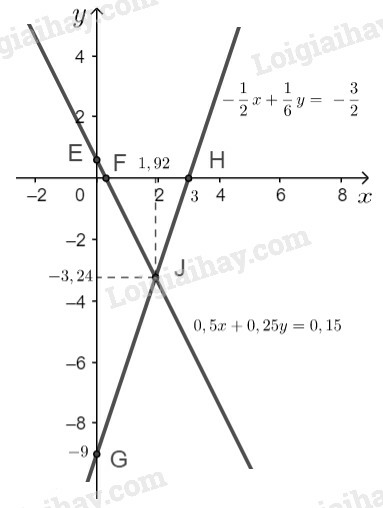
- Tìm tọa độ giao điểm:
Hoành độ giao điểm của hai đường thẳng và là nghiệm của phương trình:
Suy ra tung độ giao điểm là
Vậy tọa độ giao điểm của hai đường thẳng đã cho là
c)
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Ta có
- Từ và suy ra hai đường thẳng đã cho trùng nhau. Do đó hai đường thẳng này có vô số điểm chung.
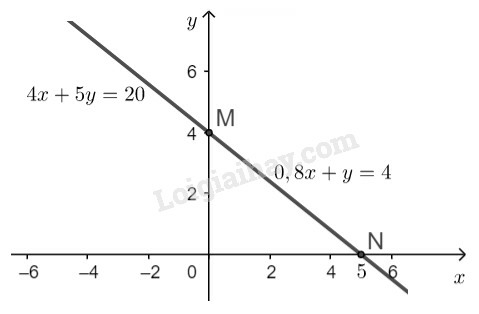
d)
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
- Ta có
Cho ta được
Cho ta được
Đường thẳng là đường thẳng đi qua hai điểm .
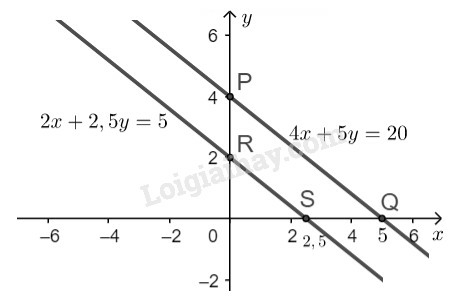
- Hai đường thẳng đã cho có hệ số góc bằng nhau, tung độ gốc khác nhau nên chúng song song với nhau. Do đó hai đường thẳng đã cho không có tọa độ giao điểm.
Sử dụng:
- Điểm thuộc đường thẳng .
Lời giải:
Điểm là giao điểm của hai đường thẳng và nên thuộc cả hai đường thẳng trên.
Vì điểm thuộc đường thẳng nên tọa độ của nó thỏa mãn phương trình đường thẳng này, ta có:
Vì thuộc đường thẳng nên tọa độ của nó thỏa mãn phương trình đường thẳng này, ta có:
Vậy là nghiệm chung của hai phương trình và .
Bài tập bổ sung (trang 6 SBT Toán 9)
Bài 1.1 trang 6 SBT Toán 9 tập 2: Điểm nào sau đây thuộc đường thẳng
Phương pháp giải:
Sử dụng:
- Điểm thuộc đường thẳng
Lời giải:
- Thay vào phương trình ta được:
(vô lí)
Do đó điểm không thuộc đường thẳng
- Thay vào phương trình ta được:
(vô lí)
Do đó điểm không thuộc đường thẳng
- Thay vào phương trình ta được:
(luôn đúng)
Do đó điểm thuộc đường thẳng
- Thay vào phương trình ta được:
(vô lí)
Do đó điểm không thuộc đường thẳng
Vậy điểm thuộc đường thẳng
Phương pháp giải:
Sử dụng:
- Đường thẳng đi qua điểm
Lời giải:
Vì đường thẳng đi qua điểm nên
Vì đường thẳng đi qua điểm nên
Do đó đường thẳng phải tìm là . Vì đường thẳng được xác định nên không đồng thời bằng , do đó .
Khi đó:
Vậy phương trình đường thẳng là:
Vì đường thẳng đi qua điểm nên
Vì đường thẳng đi qua điểm nên
Do đó đường thẳng phải tìm là: . Vì đường thẳng được xác định nên không đồng thời bằng , do đó .
Khi đó:
Vậy phương trình đường thẳng là: