Với Giải toán 10 trang 77 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải toán 10 trang 77 Tập 1 Chân trời sáng tạo
Vận dụng 2 trang 77 Toán lớp 10: Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.
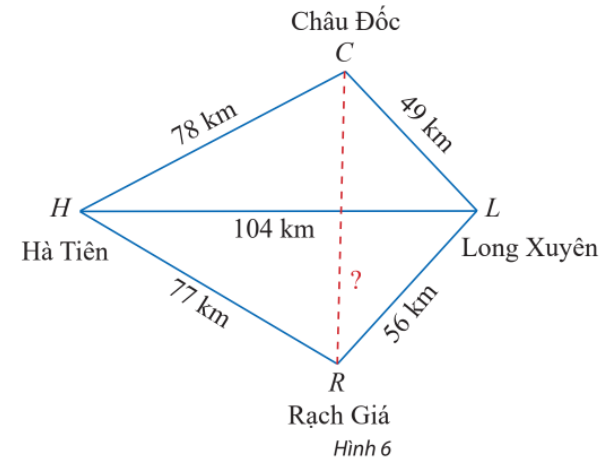
Phương pháp giải:
Bước 1: Áp dụng hệ quả của định lí cosin để tính các góc
Bước 2: Áp dụng định lí cosin
Lời giải:
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:
Bước 2: Áp dụng định lí cosin
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.
Bài 1 trang 77 Toán lớp 10: Giải tam giác ABC trong các trường hợp sau:
a)
b)
c)
d)
Lời giải:
a)
Ta cần tính cạnh BC và hai góc
Áp dụng định lí cosin, ta có:
Áp dụng định lí sin, ta có:
b)
Ta cần tính góc A và hai cạnh AB, AC.
Ta có:
Áp dụng định lí sin, ta có:
c)
Ta cần tính góc A và hai cạnh AB, BC.
Ta có:
Áp dụng định lí sin, ta có:
d)
Ta cần tính số đo ba góc
Áp dụng hệ quả của định lí cosin, ta có:
Bài 2 trang 77 Toán lớp 10: Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
Phương pháp giải:
Bước 1: Tính cạnh AB: Áp dụng định lí cosin:
Bước 2: Tính chiều dài tăng thêm, bằng
Lời giải:
Áp dụng định lí cosin, ta có:
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
Bài 3 trang 77 Toán lớp 10: Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5° (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.
Phương pháp giải:
Kí hiệu các điểm A, B, C như hình dưới.
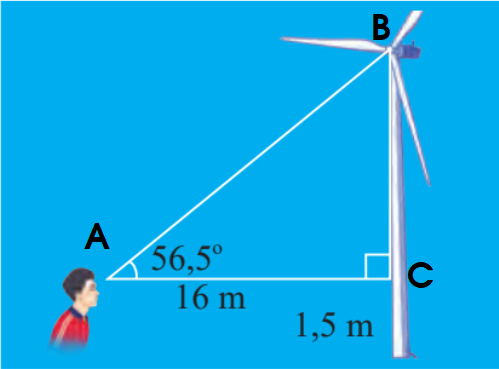
Cách 1:
Tính góc B rồi áp dụng định lí sin để tính BC:
Cách 2:
Lời giải:
Kí hiệu các điểm A, B, C như hình dưới.

Cách 1:
Ta có:
Áp dụng định lí sin, ta có:
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
Cách 2:
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Giải toán lớp 10 trang 74 Tập 1
Giải toán lớp 10 trang 75 Tập 1
Giải toán lớp 10 trang 76 Tập 1
Giải toán lớp 10 trang 78 Tập 1