Giải toán 10 trang 65 Tập 1 Chân trời sáng tạo

Lữ Ngọc My My Ngày: 17-02-2023 Lớp 10

316

Với Giải toán 10 trang 65 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 65 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 65 Toán lớp 10: a) Tính $\cos 80 ° 43' 51''$ ; $\tan 147 ° 12' 25''$ ; $c o t 99 ° 9' 19''$

b) Tìm $α (0 ° \leq α \leq 180 °)$ , biết $\cos α = - 0, 723$

Phương pháp giải:

a) Sử dụng máy tính cầm tay, bấm liên tiếp các phím:

Để tính $\cot 99^{o} 9^{'} 19^{″}$ ta tính $1 : \tan 99^{o} 9^{'} 19^{″}$ .

b) Sử dụng máy tính cầm tay, bấm liên tiếp các phím:

Lời giải:

$\begin{array}{l} \cos 80^{o} 43^{'} 51^{″} = 0, 161; \\ \tan 147^{o} 12^{'} 25^{″} = - 0, 644; \\ \cot 99^{o} 9^{'} 19^{″} = - 0, 161 \end{array}$

b) $α = 136^{o} 18^{'} 9, 81^{″} .$

Bài 1 trang 65 Toán lớp 10: Cho biết sin 30° = $\frac{1}{2}$ ; sin60° = $\frac{\sqrt{3}}{2}$ ; tan45° = 1. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của E = 2cos30° + sin150° + tan135°.

Phương pháp giải:

$\begin{array}{l} \cos 30^{o} = \sin (90^{o} - 30^{o}) = \sin 60^{o} \\ \sin 150^{o} = \sin (180^{o} - 150^{o}) = \sin 30^{o} \\ \tan 135^{o} = - \tan (180^{o} - 135^{o}) = - \tan 45^{o} \end{array}$

Lời giải:

Ta có:

$\begin{array}{l} \cos 30^{o} = \sin (90^{o} - 30^{o}) = \sin 60^{o} = \frac{\sqrt{3}}{2}; \\ \sin 150^{o} = \sin (180^{o} - 150^{o}) = \sin 30^{o} = \frac{1}{2}; \\ \tan 135^{o} = - \tan (180^{o} - 135^{o}) = - \tan 45^{o} = - 1 \end{array}$

$\Rightarrow E = 2. \frac{\sqrt{3}}{2} + \frac{1}{2} - 1 = \sqrt{3} - \frac{1}{2} .$

Bài 2 trang 65 Toán lớp 10: Chứng minh rằng:

a) sin20° = sin160°;

b) cos50° = – cos130°.

Phương pháp giải:

$\begin{array}{l} \sin (180^{o} - α) = \sin α \\ \cos (180^{o} - α) = - \cos α \end{array}$ $(0^{o} \leq α \leq 180^{o})$

Lời giải:

a) $\sin 20^{o} = \sin (180^{o} - 160^{o}) = \sin 160^{o}$

b) $\cos 50^{o} = \cos (180^{o} - 130^{o}) = - \cos 130^{o}$

Bài 3 trang 65 Toán lớp 10: Tìm α (0° ≤ α ≤ 180°) trong mỗi trường hợp sau:

a) cosα = $\frac{- \sqrt{2}}{2}$ ;

b) sinα = 0;

c) tanα = 1;

d) cotα không xác định.

Phương pháp giải:

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt để tìm góc.

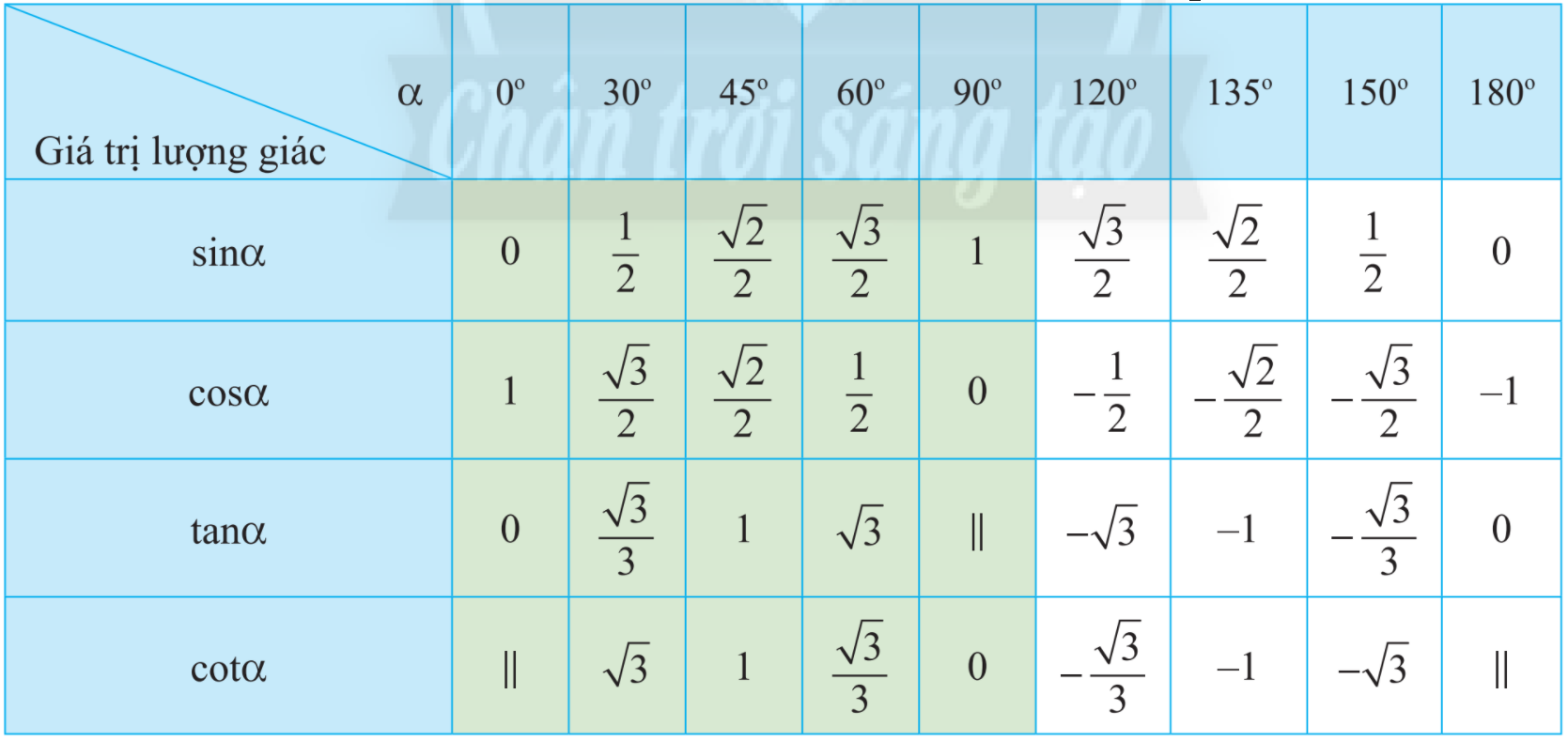
Lời giải:

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos α$ ta có:

$\cos α = \frac{- \sqrt{2}}{2}$ với $α = 135^{o}$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin α$ ta có:

$\sin α = 0$ với $α = 0^{o}$ và $α = 180^{o}$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan α$ ta có:

$\tan α = 1$ với $α = 45^{o}$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot α$ ta có:

$\cot α$ không xác định với $α = 0^{o}$

Bài 4 trang 65 Toán lớp 10: Cho tam giác ABC. Chứng minh rằng:

a) sinA = sin(B + C);

b) cosA = – cos(B + C).

Phương pháp giải:

$\begin{array}{l} \sin (180^{o} - A) = \sin A \\ \cos (180^{o} - A) = - \cos A \end{array}$ $(0^{o} \leq \hat{A} \leq 180^{o})$

Lời giải:

$\sin (B + C) = \sin (180^{o} - A) = \sin A$

Vậy $\sin A = \sin (B + C)$

$\cos (B + C) = \cos (180^{o} - A) = - \cos A$

Vậy $\cos A = - \cos (B + C)$

Bài 5 trang 65 Toán lớp 10: Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:

a) cos2α + sin2α = 1;

b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).

c) 1 + tan2α = $\frac{1}{\cos^{2} α}$ (α ≠ 90°);

d) 1 + cot2 α = $\frac{1}{\sin^{2} α}$ (0° < α < 180°).

Lời giải:

a) $\cos^{2} α + \sin^{2} α = 1$

Trên nửa đường tròn đơn vị, lấy điểm M sao cho $\hat{x O M} = α$

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

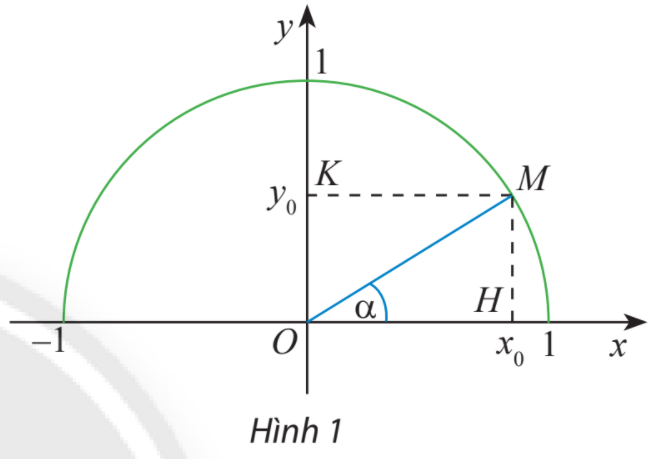
Ta có: tam giác vuông OHM vuông tại H và $α = \hat{x O M}$

Do đó: $\sin α = \frac{M H}{O M} = M H; \cos α = \frac{O H}{O M} = O H .$

$\Rightarrow \cos^{2} α + \sin^{2} α = O H^{2} + M H^{2} = O M^{2} = 1$

b) $\tan α . \cot α = 1 (0^{o} < α < 180^{o}, α \neq 90^{o})$

Ta có:

$\begin{array}{l} \tan α = \frac{\sin α}{\cos α}; \cot α = \frac{\cos α}{\sin α} . \\ \Rightarrow \tan α . \cot α = \frac{\sin α}{\cos α} . \frac{\cos α}{\sin α} = 1 \end{array}$

c) $1 + \tan^{2} α = \frac{1}{\cos^{2} α} (α \neq 90^{o})$

Với $α \neq 90^{o}$ ta có:

$\begin{array}{l} \tan α = \frac{\sin α}{\cos α}; \\ \Rightarrow 1 + \tan^{2} α = 1 + \frac{\sin^{2} α}{\cos^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\cos^{2} α} = \frac{1}{\cos^{2} α} \end{array}$

d) $1 + \cot^{2} α = \frac{1}{\sin^{2} α} (0^{o} < α < 180^{o})$

Ta có:

$\begin{array}{l} \cot α = \frac{\cos α}{\sin α}; \\ \Rightarrow 1 + \cot^{2} α = 1 + \frac{\cos^{2} α}{\sin^{2} α} = \frac{\sin^{2} α + \cos^{2} α}{\sin^{2} α} = \frac{1}{\sin^{2} α} \end{array}$

Bài 6 trang 65 Toán lớp 10: Cho góc α với cosα = $- \frac{\sqrt{2}}{2}$ . Tính giá trị của biểu thức A = 2sin2α + 5cos2α .

Phương pháp giải:

Sử dụng đẳng thức $\cos^{2} α + \sin^{2} α = 1$

Lời giải:

Ta có: $A = 2 \sin^{2} α + 5 \cos^{2} α = 2 (\sin^{2} α + \cos^{2} α) + 3 \cos^{2} α$

Mà $\cos^{2} α + \sin^{2} α = 1; \cos α = - \frac{\sqrt{2}}{2} .$

$\Rightarrow A = 2 + 3. {(- \frac{\sqrt{2}}{2})}^{2} = 2 + 3. \frac{1}{2} = \frac{7}{2} .$

Bài 7 trang 65 Toán lớp 10: Dùng máy tính cầm tay, hãy thực hiện các yêu cầu dưới đây:

a) Tính: sin168°45'33"; cos17°22'35"; tan156°26'39"; cot 56°36'42".

b) Tìm α (0° ≤ α ≤ 180°) trong các trường hợp sau:

i) sinα = 0,862;

ii) cosα = – 0,567;

iii) tanα = 0,334.

Phương pháp giải:

a) Để tính $\sin 168^{o} 45^{'} 33^{″}$ , bấm liên tiếp các phím:

Để tính $\cot 56^{o} 36^{'} 42^{″}$ ta tính $1 : \tan 56^{o} 36^{'} 42^{″}$ .

b) Để tìm $α$ biết $\sin α = 0, 862$ , bấm liên tiếp các phím:

Lời giải:

$\begin{array}{l} \sin 168^{o} 45^{'} 33^{″} = 0, 195; \\ \cos 17^{o} 22^{'} 35^{″} = 0, 954; \\ \tan 156^{o} 26^{'} 39^{″} = - 0, 436; \\ \cot 56^{o} 36^{'} 42^{″} = 0, 659 \end{array}$