Giải toán 10 trang 56 Tập 1 Chân trời sáng tạo

Lữ Ngọc My My Ngày: 17-02-2023 Lớp 10

456

Với Giải toán 10 trang 56 Tập 1 Chân trời sáng tạo chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải toán 10 trang 56 Tập 1 Chân trời sáng tạo

Bài 1 trang 56 Toán lớp 10: Hàm số nào sau đây là hàm số bậc hai?

a) $y = 9 x^{2} + 5 x + 4$

b) $y = 3 x^{3} + 2 x + 1$

c) $y = - 4 {(x + 2)}^{3} + 2 (2 x^{3} + 1) + 5$

d) $y = 5 x^{2} + \sqrt{x} + 2$

Phương pháp giải:

Hai số bậc hai (biến x) có dạng $y = f (x) = a x^{2} + b x + c$ với $a, b, c \in R$ và $a \neq 0$

Lời giải:

Hàm số ở câu a) $y = 9 x^{2} + 5 x + 4$ là hàm số bậc hai với $a = 9, b = 5, c = 4$

Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa $x^{3}$

Hàm số ở câu d) $y = 5 x^{2} + \sqrt{x} + 2$ không phải là hàm số bậc hai vì chứa $\sqrt{x}$

Bài 2 trang 56 Toán lớp 10: Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai.

a) $y = m x^{4} + (m + 1) x^{2} + x + 3$

b) $y = (m - 2) x^{3} + (m - 1) x^{2} + 5$

Phương pháp giải:

Hai số bậc hai (biến x) có dạng $y = f (x) = a x^{2} + b x + c$ với $a, b, c \in R$ và $a \neq 0$

Điều kiện: Bậc hai, hệ số a khác 0.

Lời giải:

a) Để hàm số $y = m x^{4} + (m + 1) x^{2} + x + 3$ là hàm số bậc hai thì:

${\begin{cases} m = 0 \\ m + 1 \neq 0 \end{cases}$ tức là $m = 0.$

Khi đó $y = x^{2} + x + 3$

Vây $m = 0$ thì hàm số đã cho là hàm số bậc hai $y = x^{2} + x + 3$

b) Để hàm số $y = (m - 2) x^{3} + (m - 1) x^{2} + 5$ là hàm số bậc hai thì:

${\begin{cases} m - 2 = 0 \\ m - 1 \neq 0 \end{cases}$ tức là $m = 2.$

Khi đó $y = (2 - 1) x^{2} + 5 = x^{2} + 5$

Vây $m = 2$ thì hàm số đã cho là hàm số bậc hai $y = x^{2} + 5$

Bài 3 trang 56 Toán lớp 10: Lập bảng biến thiên của hàm số $y = x^{2} + 2 x + 3.$ Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

Phương pháp giải:

Với $a = 1 > 0$ , hàm số có bảng biến thiên dạng:

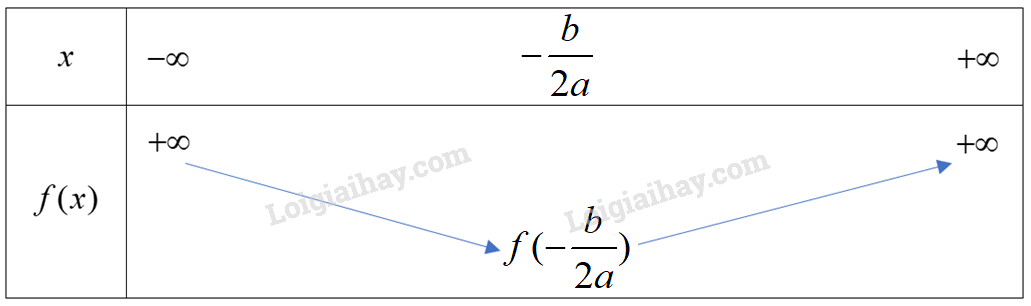
Hàm số đạt giá trị nhỏ nhất bằng $f (- \frac{b}{2 a})$ tại $x = - \frac{b}{2 a} .$

Lời giải:

Đỉnh S có tọa độ: $x_{S} = \frac{- b}{2 a} = \frac{- 2}{2.1} = - 1; y_{S} = {(- 1)}^{2} + 2. (- 1) + 3 = 2.$

Hay $S (- 1; 2) .$

Vì hàm số bậc hai có $a = 1 > 0$ nên ta có bảng biến thiên sau:

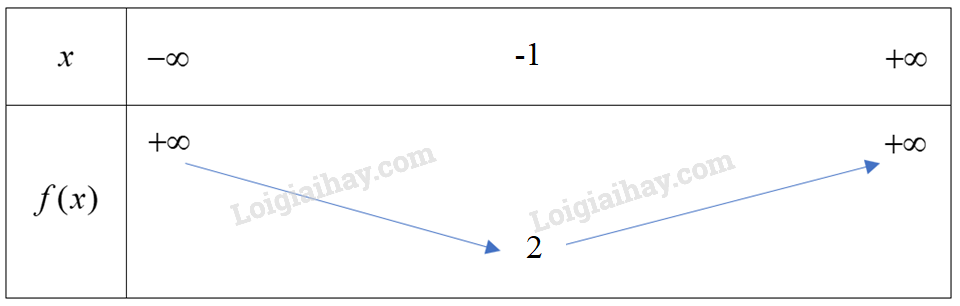
Hàm số đạt giá trị nhỏ nhất bằng $2$ .

Bài 4 trang 56 Toán lớp 10: Cho hàm số bậc hai $y = f (x) = a x^{2} + b x + c$ có $f (0) = 1, f (1) = 2, f (2) = 5.$

a) Hãy xác định giá trị của các hệ số $a, b$ và $c .$

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Phương pháp giải:

a) $f (0) = a {.0}^{2} + b .0 + c = 1$ , từ đó suy ra c.

Tương tự, sử dụng giả thiết $f (1) = 2, f (2) = 5,$ lập hệ phương trình 2 ẩn a, b.

b) Tập giá trị $T = {f (x) | x \in D}$ với D là tập xác định của hàm số $f (x) .$

Với $a = 1 > 0$ :
Hàm số nghịch biến trên khoảng $(- \infty; - \frac{b}{2 a})$ và đồng biến trên khoảng $(- \frac{b}{2 a}; + \infty)$

Lời giải:

a) Ta có: $f (0) = a {.0}^{2} + b .0 + c = 1 \Rightarrow c = 1.$

Lại có:

$f (1) = a {.1}^{2} + b .1 + c = 2 \Rightarrow a + b + 1 = 2$

$f (2) = a {.2}^{2} + b .2 + c = 5 \Rightarrow 4 a + 2 b + 1 = 5$

Từ đó ta có hệ phương trình ${\begin{cases} a + b + 1 = 2 \\ 4 a + 2 b + 1 = 5 \end{cases}$

$\Leftrightarrow {\begin{cases} a + b = 1 \\ 4 a + 2 b = 4 \end{cases} \Leftrightarrow {\begin{cases} a = 1 \\ b = 0 \end{cases}$ (thỏa mãn điều kiện $a \neq 0$ )

Vậy hàm số bậc hai đó là $y = f (x) = x^{2} + 1$

b) Tập giá trị $T = {x^{2} + 1 | x \in R}$

Vì $x^{2} + 1 \geq 1 \forall x \in R$ nên $T = [1; + \infty)$

Đỉnh S có tọa độ: $x_{S} = \frac{- b}{2 a} = \frac{- 0}{2.1} = 0; y_{S} = f (0) = 1$

Hay $S (0; 1) .$

Vì hàm số bậc hai có $a = 1 > 0$ nên ta có bảng biến thiên sau:

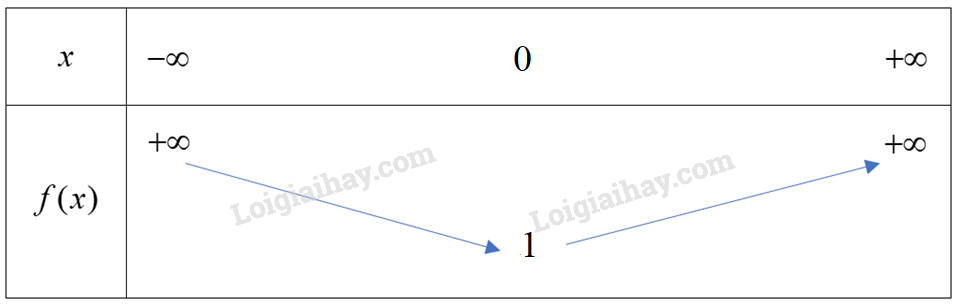
Hàm số nghịch biến trên khoảng $(- \infty; 0)$ và đồng biến trên khoảng $(0; + \infty)$

Bài 5 trang 56 Toán lớp 10: Cho hàm số $y = 2 x^{2} + x + m$ . Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.

Phương pháp giải:

Đỉnh S có tọa độ: $x_{S} = \frac{- b}{2 a}; y_{S} = f (\frac{- b}{2 a})$

$a = 2 > 0$ nên ta có bảng biến thiên sau:

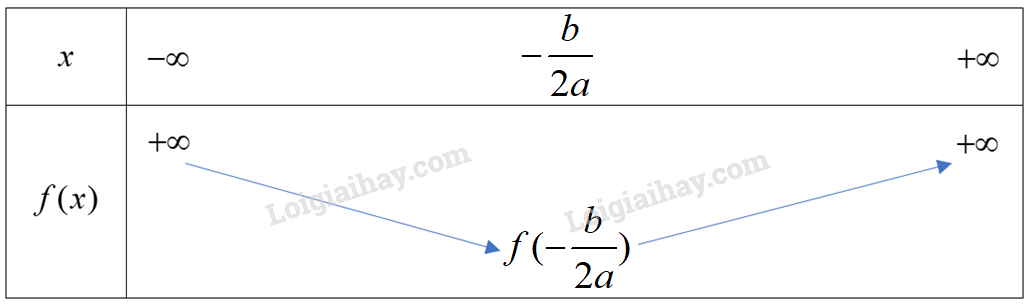
Hàm số đạt giá trị nhỏ nhất bằng $f (- \frac{b}{2 a})$ tại $x = - \frac{b}{2 a} .$

=> Tìm m để $f (- \frac{b}{2 a}) = 5$

Lời giải:

Đỉnh S có tọa độ: $x_{S} = \frac{- b}{2 a} = \frac{- 1}{2.2} = - \frac{1}{4}; y_{S} = f (- \frac{1}{4}) = 2 {(- \frac{1}{4})}^{2} + (- \frac{1}{4}) + m = m - \frac{1}{8}$

Ta có: $a = 2 > 0$ , hàm số có bảng biến thiên dạng:

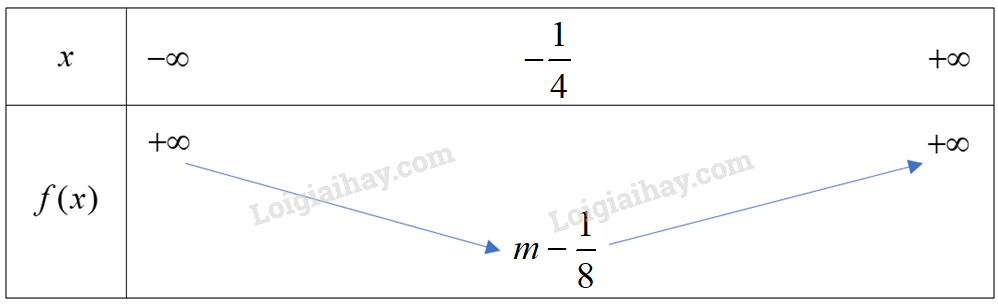
Hàm số đạt giá trị nhỏ nhất bằng $m - \frac{1}{8} = 5 \Leftrightarrow m = \frac{41}{8} .$

Vậy $m = \frac{41}{8}$ thì hàm số đạt giá trị nhỏ nhất bằng 5.

Bài 6 trang 56 Toán lớp 10: Vẽ đồ thị các hàm số sau:

a) $y = 2 x^{2} + 4 x - 1$

b) $y = - x^{2} + 2 x + 3$

c) $y = - 3 x^{2} + 6 x$

d) $y = 2 x^{2} - 5$

Lời giải:

a) $y = 2 x^{2} + 4 x - 1$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = 2 x^{2} + 4 x - 1$ là một parabol (P):

+ Có đỉnh S với hoành độ: $x_{S} = \frac{- b}{2 a} = \frac{- 4}{2.2} = - 1; y_{S} = 2. (- 1)^{2} + 4. (- 1) - 1 = - 3.$

+ Có trục đối xứng là đường thẳng $x = - 1$ (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì $a = 2 > 0$

+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).

Ta vẽ được đồ thị như hình dưới.

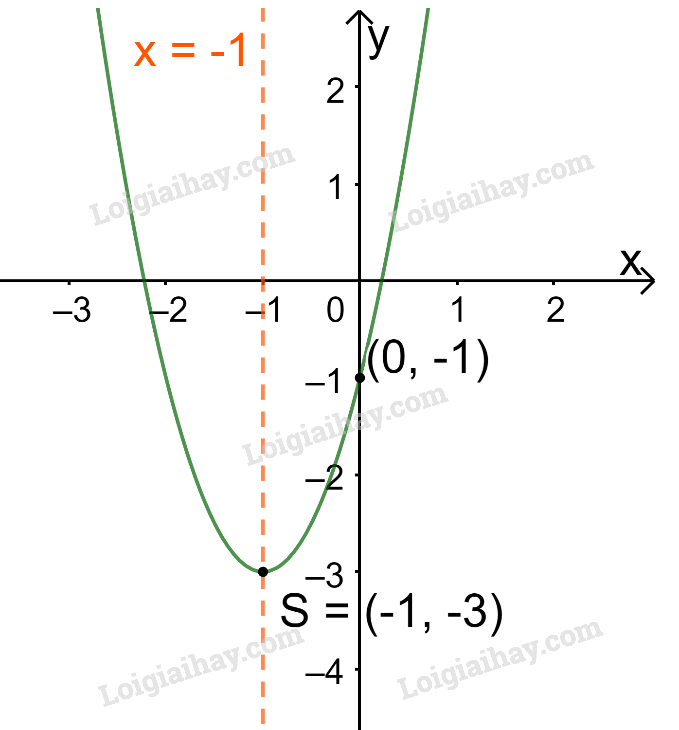
b) $y = - x^{2} + 2 x + 3$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = - x^{2} + 2 x + 3$ là một parabol (P):

+ Có đỉnh S với hoành độ: $x_{S} = \frac{- b}{2 a} = \frac{- 2}{2. (- 1)} = 1; y_{S} = - 1^{2} + 2.1 + 3 = 4.$

+ Có trục đối xứng là đường thẳng $x = 1$ (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì $a = - 1 < 0$

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

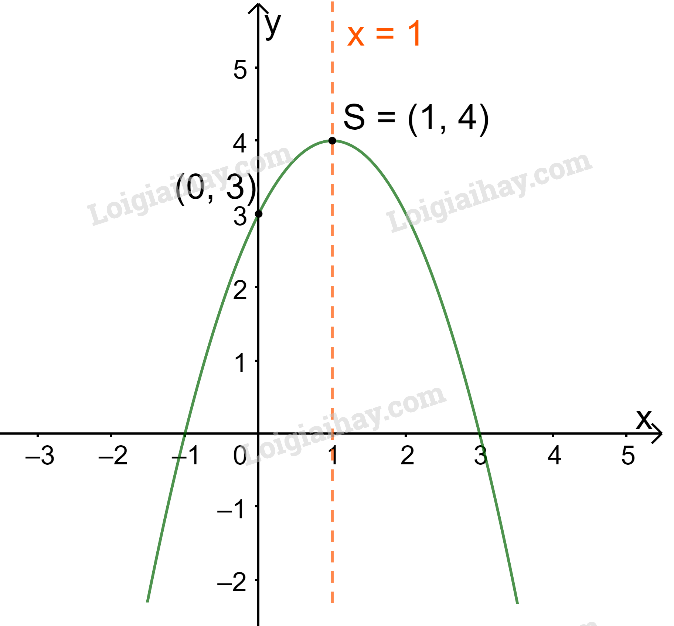
c) $y = - 3 x^{2} + 6 x$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = - 3 x^{2} + 6 x$ là một parabol (P):

+ Có đỉnh S với hoành độ: $x_{S} = \frac{- b}{2 a} = \frac{- 6}{2. (- 3)} = 1; y_{S} = - {3.1}^{2} + 6.1 = 3$

+ Có trục đối xứng là đường thẳng $x = 1$ (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay xuống dưới vì $a = - 3 < 0$

+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).

Ta vẽ được đồ thị như hình dưới.

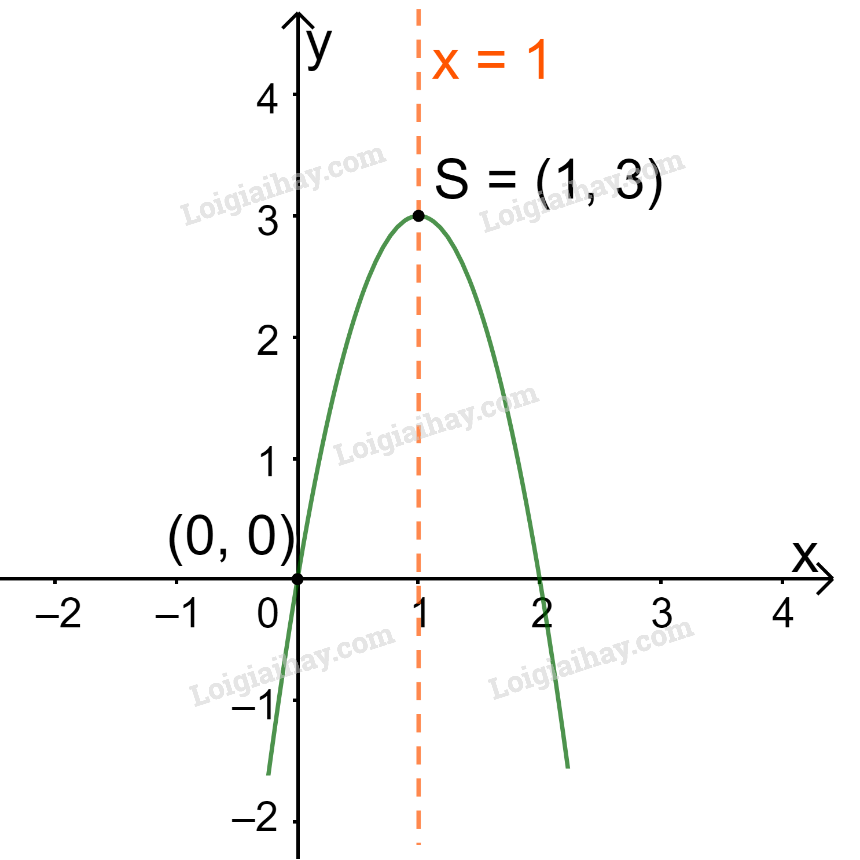
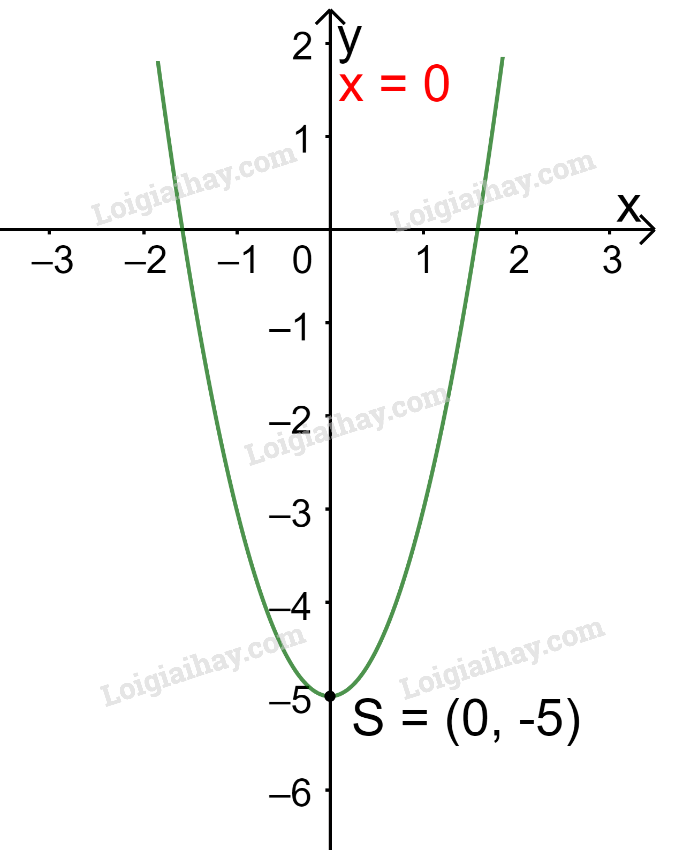
d) $y = 2 x^{2} - 5$

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai $y = 2 x^{2} - 5$ là một parabol (P):

+ Có đỉnh S với hoành độ: $x_{S} = \frac{- b}{2 a} = \frac{- 0}{2.2} = 0; y_{S} = {2.0}^{2} - 5 = - 5.$

+ Có trục đối xứng là đường thẳng $x = 0$ (trùng với trục Oy);

+ Bề lõm quay lên trên vì $a = 2 > 0$

+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).

Ta vẽ được đồ thị như hình dưới.

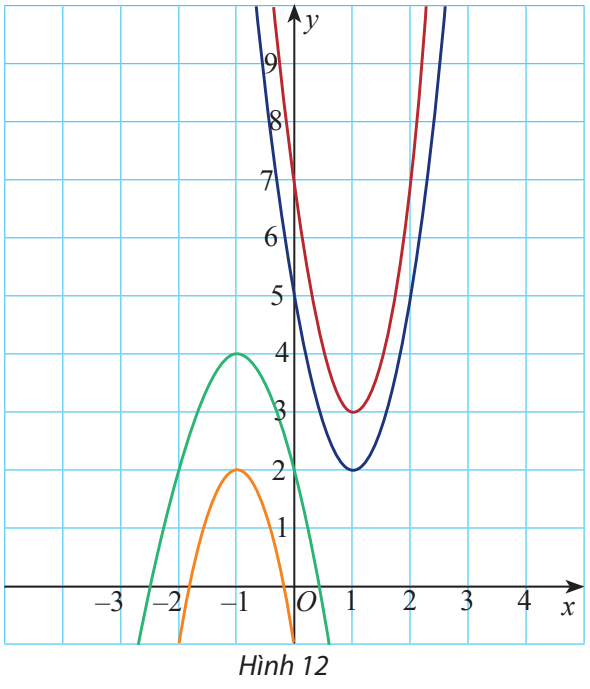
Bài 7 trang 56 Toán lớp 10: Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.

$\begin{array}{l} (P_{1}) : y = - 2 x^{2} - 4 x + 2; \\ (P_{2}) : y = 3 x^{2} - 6 x + 5; \\ (P_{3}) : y = 4 x^{2} - 8 x + 7; \\ (P_{4}) : y = - 3 x^{2} - 6 x - 1. \end{array}$

Phương pháp giải:

+ Xác định tọa độ giao điểm với trục tung: điểm có tọa độ (0; c).

Lời giải:

Vì 4 đồ thị hàm số cắt trục tung tại 4 điểm phân biệt nên ta chỉ cần xác định tọa độ giao điểm của mỗi hàm số với trục tung là có thể phân biệt 4 đồ thị hàm số.

Đồ thị hàm số $(P_{1}) : y = - 2 x^{2} - 4 x + 2$ cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2) => Đồ thị là đường màu xanh lá.

Đồ thị hàm số $(P_{2}) : y = 3 x^{2} - 6 x + 5;$ cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5) => Đồ thị là đường màu xanh dương.

Đồ thị hàm số $(P_{3}) : y = 4 x^{2} - 8 x + 7;$ cắt trục tung tại điểm có tung độ bằng 7, tức là đồ thị đi qua điểm có tọa độ (0; 7) => Đồ thị là đường màu nâu đỏ.

Đồ thị hàm số $(P_{4}) : y = - 3 x^{2} - 6 x - 1$ cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1) => Đồ thị là đường màu vàng.