Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
Phương pháp giải:
Sử dụng tính chất tam giác cân và tỉ số lượng giác của góc nhọn.
Cho tam giác vuông tại thì
Lời giải:
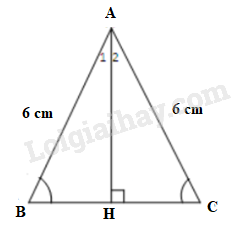
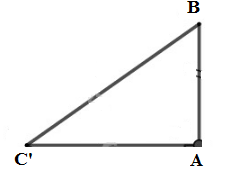
Vì các cạnh của tam giác lần lượt là và nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh
Giả sử tam giác cân tại có cạnh bên và cạnh đáy Ta tính góc
Kẻ đường cao tại
Vì tam giác cân nên đường cao vừa là đường trung tuyến vừa là đường phân giác.
Suy ra là trung điểm của nên
Xét tam giác vuông tại theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
Suy ra
Mà là phân giác góc (cmt) nên
Vậy góc nhỏ nhất của tam giác bằng .
a) ; b) ;
c) Phân giác
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
b) Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Suy ra cạnh huyền bằng cạnh góc vuông chia sin góc đồi hoặc chia cos góc kề.
Lời giải:
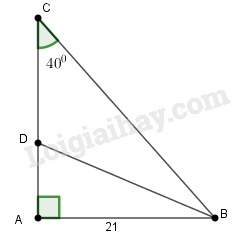
a) Trong tam giác vuông ABC ta có:
b) Trong tam giác vuông ABC ta có:
c) Vì vuông tại nên
Suy ra:
Vì là phân giác của góc nên:
Trong tam giác vuông , ta có:
Biết:
và Tính
a) Độ dài cạnh
b) ;
c) Khoảng cách từ điểm đến cạnh
Phương pháp giải:
Cho hình vẽ:
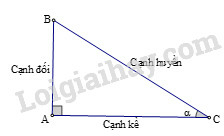
Ta có:
Lời giải:
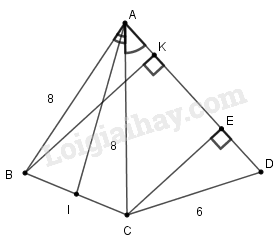
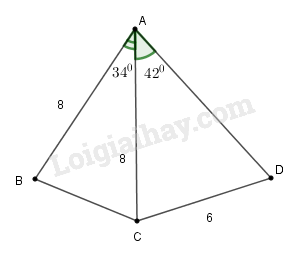
a) Kẻ
Vì cân tại A nên AI vừa là đường cao, vừa là đường trung tuyến, đường phân giác nên:
và
Trong tam giác vuông , ta có:
b) Kẻ
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
c) Kẻ
Trong tam giác vuông , ta có:
Phương pháp giải:
Cho hình vẽ:
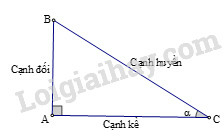
Ta có:
Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
Lời giải:
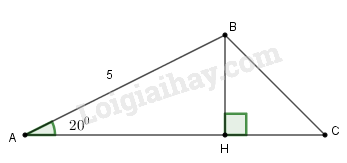
Kẻ tại
Trong tam giác vuông , ta có:
Ta có:
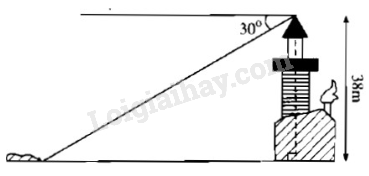
Phương pháp giải:
Cho hình vẽ:
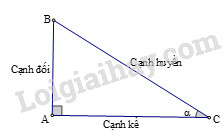
Ta có:
Lời giải:
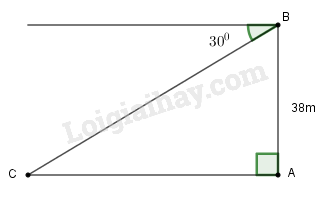
Đặt tên như hình vẽ.
Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc chiều cao của cột đèn biển là cạnh đối diện với góc Ta có . Ta tính AC.
Xét tam giác ABC vuông tại A, ta có:
Vậy khoảng cách từ đảo đến chân đèn là:
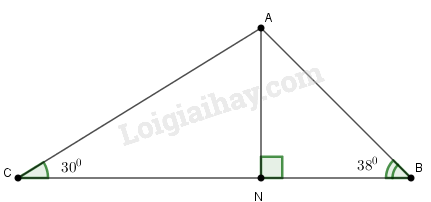
Phương pháp giải:
Cho hình vẽ:
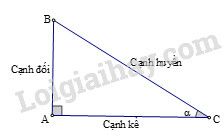
Ta có: nên và
Lời giải:
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
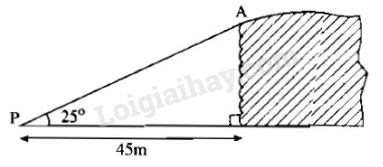
Phương pháp giải:
Cho hình vẽ:
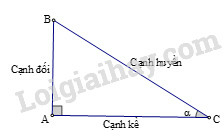
Ta có:
Lời giải:
Chiều cao vách đá là cạnh góc vuông đối diện với góc 25° . Khi đó chiều cao của vách đá là:
a)
b)
c)
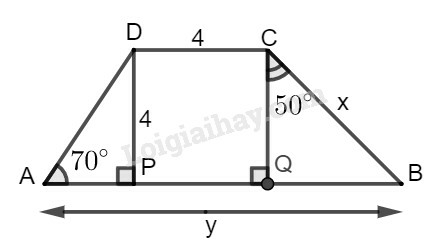
Phương pháp giải:
+) Cho hình vẽ:
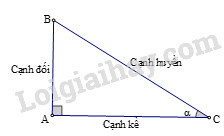
Ta có ,
+) Định lí Pytago vào tam giác vuông tại :
Lời giải:
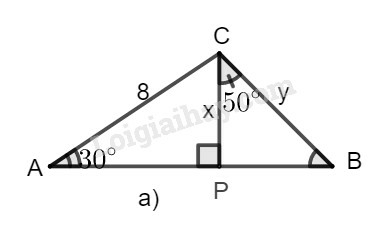
a) Hình a
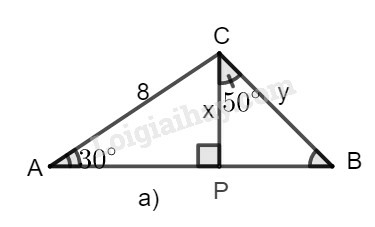
Trong tam giác vuông , ta có:
Trong tam giác vuông BCP, ta có:
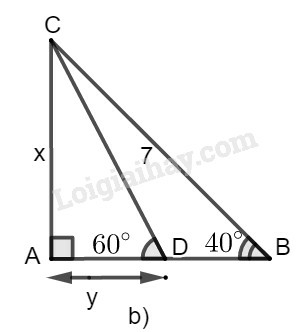
b) Hình b
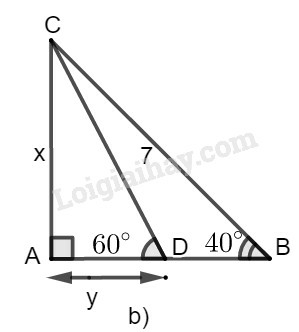
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
c) Hình c
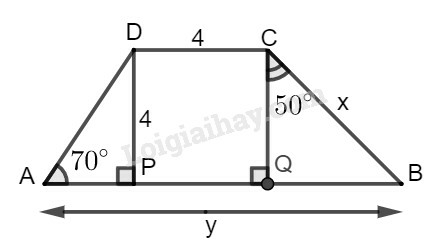
Vì tứ giác có , (vì cùng vuông với AB) nên là hình bình hành có nên là hình chữ nhật. Mà nên là hình vuông.
Suy ra:
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
Ta có:
.
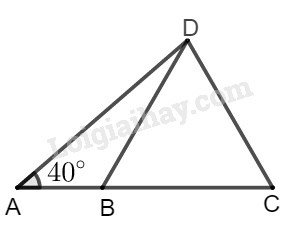
Bài 60 trang 115 SBT Toán 9 tập 1: Cho hình: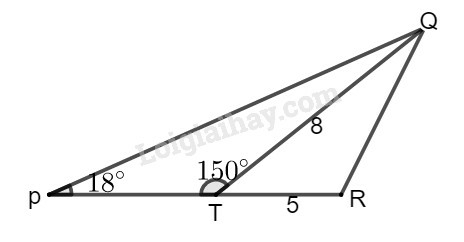
Biết:
,
,
Hãy tính:
a)
b) Diện tích tam giác
Phương pháp giải:
+) Cho hình vẽ:
Ta có:
+) Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
Lời giải:
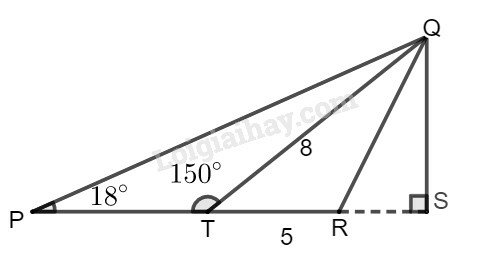
a) Kẻ
Ta có:
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
b) Ta có:
Hãy tính:
a)
b)
Phương pháp giải:
Cho hình vẽ:
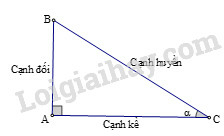
Ta có: nên và
Lời giải:
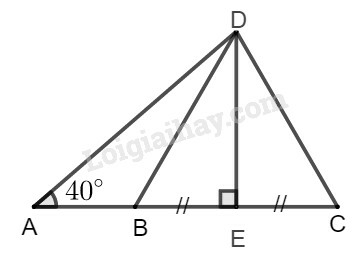
a) Kẻ
Suy ra:
Trong tam giác vuông , ta có:
Trong tam giác vuông , ta có:
b) Trong tam giác vuông , ta có:
Ta có:
Áp dụng hệ thức lượng trong tam giác có đường cao , ta có:
Sử dụng tỉ số lượng giác của góc nhọn:
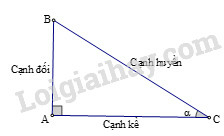
Lời giải:
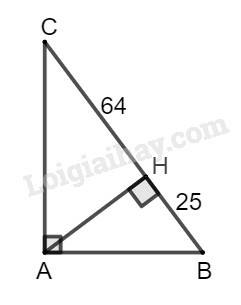
Xét tam giác ABC vuông tại A có chiều cao AH, theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
Suy ra:
(cm)
Trong tam giác vuông ABH, ta có:
Suy ra:
Vì tam giác vuông nên
Suy ra:
a) Đường cao và cạnh
b) Diện tích tam giác
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Suy ra cạnh huyền bằng cạnh góc vuông chia sin góc đồi hoặc chia cosin góc kề.
Lời giải:
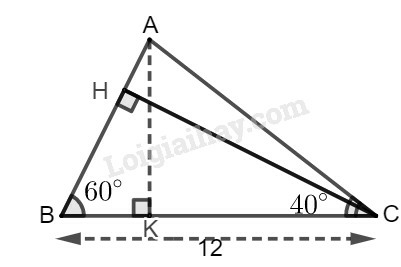
a) Trong tam giác vuông BCH, ta có:
(cm)
Trong tam giác ABC, ta có: (tổng ba góc trong tam giác bằng )
Suy ra
Trong tam giác vuông ACH, ta có:
(cm)
b) Kẻ
Trong tam giác vuông ACK, ta có:
(cm)
Vậy (cm2)
Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác vuông tại có thì:
Diện tích hình bình hành bằng tích chiều cao với cạnh đáy tương ứng.
Lời giải:
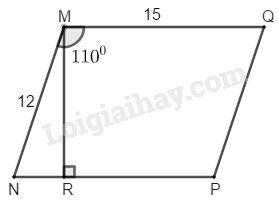
Giả sử hình bình hành có
Ta có: (hai góc trong cùng phía)
Suy ra:
Kẻ
Trong tam giác vuông ta có:
Vậy
Phương pháp giải:
Áp dụng công thức tính diện tích hình thang:
Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác vuông tại có thì:
Lời giải:
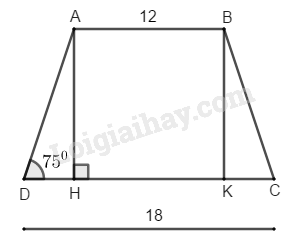
Giả sử hình thang cân có
Kẻ suy ra
Lại có nên ABKH là hình bình hành.
Suy ra:
Vì là hình thang cân nên
Nên (cạnh huyền, góc nhọn)
Suy ra:
Suy ra:
Trong tam giác vuông ta có:
Vậy:
Một cột cờ cao có bóng trên mặt đất dài Hỏi góc giữa tia sáng mặt trời và bóng cột cờ là bao nhiêu?
Phương pháp giải:
Cho tam giác vuông tại có thì:
Lời giải:
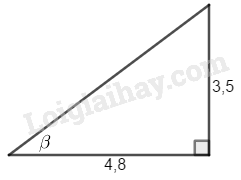
Chiều cao cột cờ là cạnh đối diện với góc giữa tia sáng mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.
Ta có:
Suy ra:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.
Lời giải:
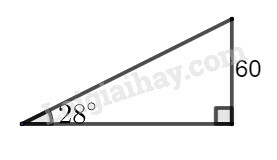
Khoảng cách từ xe ô tô đến tòa nhà là cạnh kề với góc 28, chiều cao tòa nhà là cạnh đối với góc nhọn.
Vậy chiếc ô tô đang đỗ cách tòa nhà:
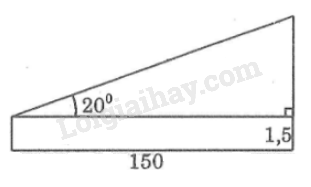
Phương pháp giải:
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.
Lời giải:
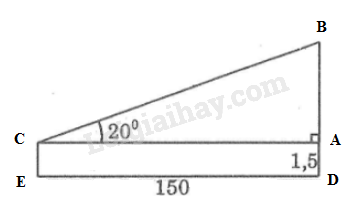
Đặt tên như hình vẽ thì chiều cao của tháp là đoạn
Xét tam giác vuông tại có nên
Chiều cao của cột ăng-ten là:
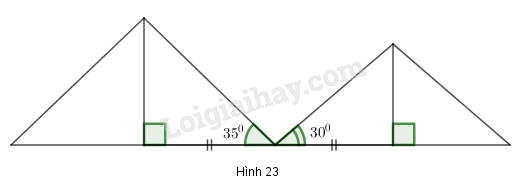
Phương pháp giải:
Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông còn lại nhân tan góc đối.
Lời giải:
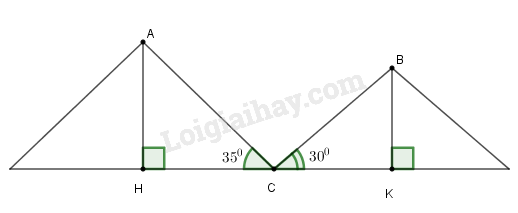
Đặt tên như hình vẽ. Khi đó chiều cao trại A là và chiều cao trại B là
Cạnh
Xét tam giác vuông tại có
Xét tam giác vuông tại có
Suy ra trại A cao hơn trại B là:
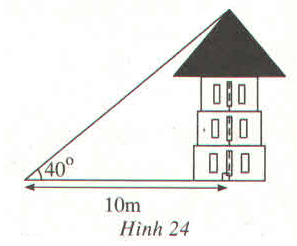
a) Tính chiều cao của tòa nhà.
b) Nếu anh ta dịch chuyển sao cho góc “nâng” là thì anh ta cách tòa nhà bao nhiêu mét?
Khi đó anh ta tiến lại gần hay ra xa ngôi nhà?
Phương pháp giải:
Trong tam giác vuông:
+ Cạnh góc vuông này bằng cạnh góc vuông kia nhân tan góc đối
+ Cạnh góc vuông này bằng cạnh góc vuông kia nhân cottan góc kề
Lời giải:
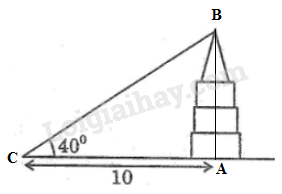
Đặt tên như hình vẽ.
a) Xét tam giác vuông tại
Chiều cao của tòa nhà là:
b) Nếu dịch chuyển sao cho góc “nâng” là thì anh ta đứng tại cách tòa nhà là:
Khi đó anh ta tiến ra xa ngôi nhà.
(h.25)
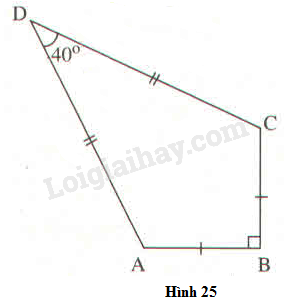
Hãy tính:
a) Chiều dài cạnh
b) Diện tích của chiếc diều.
Phương pháp giải:
+ Sử dụng định lý Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông
+ Sử dụng quan hệ giữa cạnh và góc trong tam giác vuông: Cho tam giác vuông tại thì
+ Diện tích diều
Lời giải:
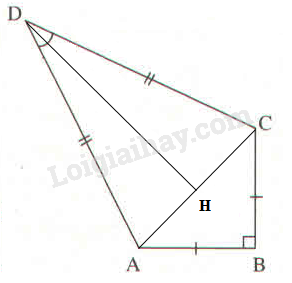
a) Nối và kẻ
Áp dụng định lí Pi-ta-go vào tam giác vuông ta có:
Suy ra:
Ta có: tam giác cân tại mà nên DH cũng là đường trung tuyến và đường phân giác của tam giác.
Suy ra:
Và
Trong tam giác vuông ta có:
b) Ta có:
Trong tam giác vuông ta có:
Mặt khác:
Vậy diện tích diều là: