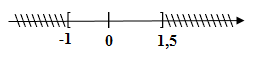Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài 68 trang 16 SBT Toán 9 tập 1: Khử mẫu của mỗi biểu thức lấy căn và rút gọn ( nếu được):
a) ;
b) với ;
c) với ;
d) với .
Phương pháp giải:
Với mà và ta có:
Lời giải:
a)
=
b)
(với )
c)
(với )
d)
(với )
Bài 69 trang 16 SBT Toán 9 tập 1: Trục căn thức ở mẫu và rút gọn (nếu được):
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Áp dụng:
với .
Lời giải:
a)
b)
c)
d)
Bài 70 trang 16 SBT Toán 9 tập 1: Rút gọn các biểu thức:
a)
b)
c)
d)
Phương pháp giải:
Quy đồng mẫu các phân thức.
Sử dụng hằng đẳng thức:
Sử dụng: với .
Lời giải:
a)
b)
c)
d)
Bài 71 trang 16 SBT Toán 9 tập 1: Chứng minh đẳng thức:
với là số tự nhiên.
Phương pháp giải:
Áp dụng:
với .
Lời giải:
Ta có:
(với là số tự nhiên)
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Bài 72 trang 17 SBT Toán 9 tập 1: Xác định giá trị biểu thức sau theo cách thích hợp:
Phương pháp giải:
Áp dụng:
với .
Lời giải:
Ta có:
Bài 73 trang 17 SBT Toán 9 tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi).
với
Phương pháp giải:
Áp dụng:
Lời giải:
Ta có:
Ta có:
Vì nên:
(3)
Từ (1), (2), (3) suy ra:
<
Bài 74 trang 17 SBT Toán 9 tập 1: Rút gọn:
Phương pháp giải:
Áp dụng:
Lời giải:
Ta có:
Bài 75 trang 17 SBT Toán 9 tập 1: Rút gọn các biểu thức:
a) với và
b) với
Phương pháp giải:
Áp dụng hằng đẳng thức:
Lời giải:
a)
Với và ta có:
b)
Với ta có:
Bài 76 trang 17 SBT Toán 9 tập 1: Trục căn thức ở mẫu:
a)
b)
Phương pháp giải:
Áp dụng:
(trong điều kiện các biểu thức có nghĩa)
Lời giải:
a)
b)
Bài 77 trang 17 SBT Toán 9 tập 1: Tìm , biết:
a)
b)
c)
d)
Phương pháp giải:
Áp dụng:
(với )
Lời giải:
a)
Vậy
b)
Vậy
c)
Vậy
d)
Ta có:
Không có giá trị nào của để .
Bài 78 trang 17 SBT Toán 9 tập 1: Tìm tập hợp các giá trị thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số:
a)
b)
Phương pháp giải:
Áp dụng:
Với ta có:
Lời giải:
a)
Điều kiện:
Ta có:
Giá trị thỏa mãn điều kiện.

b)
Điều kiện:
Ta có:
Kết hợp với điều kiện ta có:
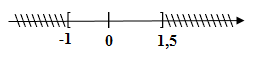
Bài 79 trang 17 SBT Toán 9 tập 1: Cho các số và có dạng: và , trong đó là các số hữu tỉ. Chứng minh:
a) và cũng có dạng với và là số hữu tỉ.
b) với cũng có dạng với và là số hữu tỉ.
Phương pháp giải:
Biến đổi, nhóm các hạng tử để đưa về dạng với và là số hữu tỉ.
Với ta có:
Với ta có:
Lời giải:
a)
Ta có:
Vì là các số hữu tỉ nên cũng là số hữu tỉ.
Lại có:
Vì là các số hữu tỉ nên , cũng là số hữu tỉ.
b)
Ta có:
Vì nên và không đồng thời bằng 0
Suy ra:
(Nếu thì
Điều này mâu thuẫn với là số vô tỉ)
Vậy ; đều là số hữu tỉ.
Bài tập bổ sung (trang 18 SBT Toán 9)
Bài 7.1 trang 18 SBT Toán 9 tập 1: Với biểu thức được biến đổi thành
(A)
(B)
(C)
(D)
Hãy chọn đáp án đúng.
Phương pháp giải:
Áp dụng:
Với
Lời giải:
Ta có:
Do nên
Vậy chọn đáp án (A).
Bài 7.2 trang 18 SBT Toán 9 tập 1: Giá trị của bằng
(A)
(B)
(C)
(D)
Hãy chọn đáp án đúng.
Phương pháp giải:
Áp dụng: Với ta có:
Lời giải:
Ta có:
Vậy đáp án (D)