Với tóm tắt lý thuyết Toán lớp 7 Chương 5: Một số yếu tố thống kê và xác suất sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.

Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất

A. Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất

1. Thu thập và phân loại dữ liệu

Trong các dữ liệu thống kê thu thập được, có những dữ liệu thống kê là số (số liệu) nhưng cũng có những dữ liệu thống kê không phải là số.

2. Tính hợp lí của dữ liệu

Sau khi thu thập, tổ chức, phân loại dữ liệu, ta cần xem xét tính hợp lí của những dữ liệu thống kê đó, đặc biệt chỉ ra được những dữ liệu không hợp lí. Ta có thể dựa trên những tiêu chí toán học đơn giản để thực hiện điều đó.

3. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ

Ở lớp 6, chúng ta đã làm quen với việc mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ (bảng số liệu, biểu đồ tranh, biểu đồ cột, biểu đồ cột kép).

Ở lớp 7, chúng ta tiếp tục tìm hiểu sâu hơn việc đọc hiểu, rút ra những thông tin cần thiết từ những dạng biểu diễn dữ liệu đã học và nhận biết những dạng biểu diễn khác nhau cho một tập dữ liệu.

4. Phân tích và xử lí dữ liệu để rút ra kết luận

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

5. Tính hợp lí của kết luận thống kê

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

6. Biểu đồ đoạn thẳng

Biểu đồ đoạn thẳng có các yếu tố sau:

+ Trục nằm ngang biểu diễn các đối tượng thống kê;

+ Trục thẳng đứng biểu diễn tiêu chí thống kê và trên trục đó đã xác định độ dài đơn vị thống kê;

+ Biểu đồ đoạn thẳng là đường gấp khúc nối từng điểm liên tiếp bằng các đoạn thẳng;

+ Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi một đối tượng thống kê và số liệu thống kê theo tiêu chí của đối tượng đó.

Chú ý:

+ Cũng như biểu đồ cột và biểu đồ cột kép, biểu đồ đoạn thẳng giúp chúng ta “trực quan hóa” một tập dữ liệu thống kê thông qua cách biểu diễn hình học tập dữ liệu đó.

+ Người ta còn biểu diễn dữ liệu thống kê ở dạng biểu đồ tương tự biểu đồ cột, trong đó các cột được thay bằng các đoạn thẳng. Biểu đồ đó cũng gọi là biểu đồ đoạn thẳng.

Nhận xét: Như ta đã biết, dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau, trong đó có biểu đồ đoạn thẳng.

7. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ đoạn thẳng

Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của tập số liệu trong một khoảng thời gian nhất định.

8. Biểu đồ hình quạt tròn

Biểu đồ hình quạt tròn có các yếu tố sau:

+ Đối tượng thống kê được biểu diễn bằng các hình quạt tròn.

+ Số liệu thống kê theo tiêu chí thống kê của mỗi đối tượng (thống kê) được ghi ở hình quạt tròn tương ứng. Số liệu thống kê đó được tính theo tỉ số phần trăm.

+ Tổng các tỉ số phần trăm ghi ở các hình quạt tròn là 100%, nghĩa là tổng các tỉ số phần trăm của các số liệu thành phần phải bằng 100% (của tổng thể thống kê).

Nhận xét:

Thông thường, trong bảng số liệu, ta có thể nhận biết nhanh chóng số liệu thống kê (theo tiêu chí) của mỗi đối tượng thống kê nhưng không biết được mỗi đối tượng đó chiếm bao nhiêu phần trăm trong tổng thể thống kê.

Ngược lại, trong biểu đồ hình quạt tròn, ta có thể nhận biết nhanh chóng mỗi đối tượng thống kê chiếm bao nhiêu phần trăm trong tổng thể thống kê nhưng lại không biết được số liệu thống kê (theo tiêu chí) của mỗi đối tượng đó.

Vì thế, tùy theo mục đích thống kê, ta sẽ lựa chọn bảng số liệu hay biểu đồ hình quạt trong để biểu diễn dữ liệu thống kê.

9. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ hình quạt tròn

Dựa trên việc biểu diễn dữ liệu bằng biểu đồ hình quạt tròn, ta có thể phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận.

10. Biến cố trong trò chơi gieo xúc xắc

Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối và đồng chất.

Mỗi xúc xắc có sáu mặt, số chấm ở mỗi mặt là một trong các số 1; 2; 3; 4; 5; 6. Gieo ngẫu nhiên xúc xắc một lần.

Nhận xét:

+ Tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:

A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” là: B = {mặt 2 chấm; mặt 4 chấm; mặt 6 chấm} (gồm ba phần tử lấy ra từ tập hợp A).

+ Trong trò chơi gieo xúc xắc, sự kiện “Mặt xuất hiện của xúc xắc có số chấm là số chẵn” còn gọi là biến cố, hay gọi đầy đủ là biến cố ngẫu nhiên. Sở dĩ ta có thêm cụm từ “ngẫu nhiên” là vì các kết quả xảy ra có tính ngẫu nhiên, ta không thể đoán trước được.

+ Mỗi kết quả: mặt 2 chấm, mặt 4 chấm, mặt 6 chấm (là phần tử của tập hợp B), được gọi là một kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chẵn”. Sở dĩ ta gọi những kết quả đó là thuận lợi cho biến cố trên vì chúng đáp ứng được mong muốn thể hiện trong biến cố, đó là mặt xuất hiện có số chấm là số chẵn.

11. Biến cố trong trò chơi rút thẻ từ trong hộp

Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

Nhận xét:

+ Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

C = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}.

+ Tập hợp các kết quả có thể xảy ra đối với sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” là: D = {4; 8; 12} (gồm ba phần tử lấy ra từ tâp hợp C).

+ Trong trò chơi rút thẻ từ trong hộp, sự kiện “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4” cũng gọi là biến cố (hay gọi đầy đủ là biến cố ngẫu nhiên).

+ Mỗi kết quả: 4; 8; 12 (là phần tử của tập hợp D), được gọi là một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.

12. Xác suất của biến cố trong trò chơi gieo xúc xắc

Trong trò chơi gieo ngẫu nhiên xúc xắc một lần:

Xác suất của một biến cố trong trò chơi gieo xúc xắc bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

Ví dụ: Gieo ngẫu nhiên xúc xắc một lần.

a) Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc.

b) Xét biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3”. Tính xác suất của biến cố đó.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là:

E = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

Vậy số phần tử của tập hợp E là 6.

b) Trong các số 1; 2; 3; 4; 5; 6, các số không chia hết cho 3 là: 1; 2; 4; 5.

Do đó có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là mặt 1 chấm; mặt 2 chấm; mặt 4 chấm; mặt 5 chấm.

Xác suất của biến cố đó là $\frac{4}{6}=\frac{2}{3}$.

Vậy xác suất của biến cố “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3” là $\frac{2}{3}$.

Chú ý: Trong trò chơi gieo xúc xắc trên, số các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là 6. Nếu k là số các kết quả thuận lợi cho biến cố thì xác suất của biến cố đó bằng $\frac{\mathrm{k}}{6}$.

13. Xác suất của biến cố trong trò chơi rút thẻ từ trong hộp

Trong trò chơi rút thẻ từ trong hộp:

Xác suất của một biến cố trong trò chơi rút thẻ từ trong hộp bằng tỉ số của số các kết quả thuận lợi cho biến cố và số các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

Ví dụ: Một hộp gồm 15 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 14; 15. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Tìm số phần tử của tập hợp F gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Xét biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1”. Tính xác suất của biến cố đó.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

F = {1; 2; 3; 4; ...; 14; 15}.

Vậy số phần tử của tập hợp F là 15.

b) Trong các số 1; 2; 3; 4; ...; 14; 15, các số chia 5 dư 1 là 1; 6; 11.

Do đó có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là 1; 6; 11.

Xác suất của biến cố đó là $\frac{3}{15}=\frac{1}{5}$.

Vậy xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia 5 dư 1” là $\frac{1}{5}$.

B. Bài tập Toán 7 Chương 5: Một số yếu tố thống kê và xác suất

B.1 Bài tập tự luận

Bài 1. Biểu đồ dưới đây cho biết số lượng sản phẩm mà một chi nhánh đã bán được trong 6 tháng đầu năm:

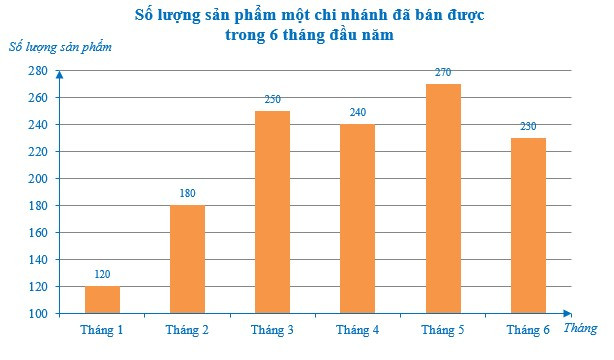
a) Số lượng sản phẩm bán được ở tháng 3 tăng bao nhiêu phần trăm so với tháng 2 (làm tròn kết quả đến hàng phần mười)?

b) Số lượng sản phẩm bán được ở tháng 6 giảm bao nhiêu phần trăm so với tháng 5 (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

a) Tỉ số phần trăm số lượng sản phẩm bán được ở tháng 3 và số lượng sản phẩm bán được ở tháng 2 là:

$\frac{250.100}{180}\%\approx 138,9\%$.

Vậy số lượng sản phẩm bán được ở tháng 3 tăng 138,9% – 100% = 38,9% so với tháng 2.

b) Tỉ số phần trăm số lượng sản phẩm bán được ở tháng 6 và số lượng sản phẩm bán được ở tháng 5 là:

$\frac{230.100}{270}\%\approx 85,2\%$.

Vậy số lượng sản phẩm bán được ở tháng 6 giảm 100% – 85,2% = 14,8% so với tháng 5.

Bài 2. Biểu đồ sau đây cho biết tổng kim ngạch xuất khẩu nông sản 2 tháng đầu năm của Việt Nam giai đoạn 2019 – 2020:

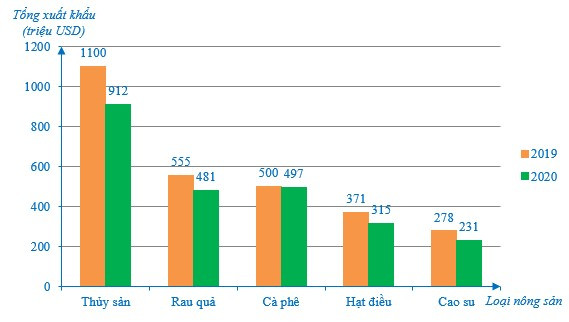
(Theo thống kê của Tổng cục Hải quan)

a) Lập bảng thống kê tổng xuất khẩu nông sản 2 tháng đầu năm giai đoạn 2019 – 2020 theo mẫu sau:

Loại nông sản Tổng xuất khẩu của năm	Thủy sản	Rau quả	Cà phê	Hạt điều	Cao su
2019	?	?	?	?	?
2020	?	?	?	?	?

b) Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2019 cao nhất? Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2020 thấp nhất?

c) Bạn An kết luận rằng: Tổng xuất khẩu thủy sản của nước ta năm 2020 giảm 18,2% so với năm 2019. Theo em, kết luận của bạn An là đúng hay sai? Vì sao?

Hướng dẫn giải

a) Dựa vào biểu đồ ta có bảng sau:

Loại nông sản Tổng xuất khẩu của năm	Thủy sản	Rau quả	Cà phê	Hạt điều	Cao su
2019	1100	555	500	371	278
2020	912	481	497	315	231

b) Nhìn vào biểu đồ cột, ta thấy:

+ Ở năm 2019, thủy sản là loại nông sản có cột biểu diễn tổng xuất khẩu cao nhất.

+ Ở năm 2020, cao su là loại nông sản có cột biểu diễn tổng xuất khẩu thấp nhất.

Vậy năm 2019 Việt Nam có tổng xuất khẩu của thủy sản cao nhất; cao su có tổng xuất khẩu năm 2020 thấp nhất.

c) Tỉ số phần trăm giữa tổng xuất khẩu thủy sản năm 2020 và tổng xuất khẩu thủy sản năm 2019 là:

$\frac{912.100}{1100}\%\approx 82,9\%$.

Do đó tổng xuất khẩu thủy sản năm 2020 giảm 100% – 82,9% = 17,1% so với năm 2019.

Ta có 17,1% ≠ 18,2%.

Vậy bạn An đã kết luận sai.

Bài 3. Biểu đồ sau đây cho biết số lượng quạt máy mà một cửa hàng đã bán được trong năm vừa qua:

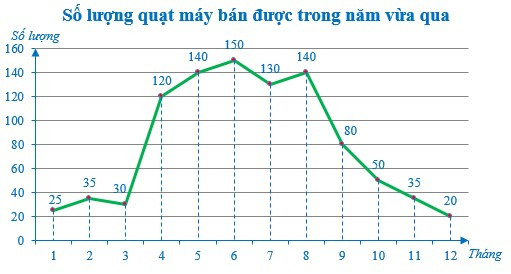
a) Tính tổng số quạt máy bán được trong năm vừa qua.

b) Tìm ba tháng bán được nhiều quạt máy nhất? Tìm ba tháng bán được ít quạt máy nhất?

c) Bạn Cường kết luận rằng: Cửa hàng buôn bán tốt vào các tháng mùa hè. Em hãy cho biết bạn Cường kết luận đúng hay sai?

Hướng dẫn giải

a) Tổng số quạt máy bán được trong năm vừa qua là:

20 + 35 + 30 + 120 + 140 + 150 + 130 + 140 + 80 + 50 + 35 + 20 = 950 (quạt máy).

Vậy tổng số quạt máy cửa hàng bán được trong năm vừa qua là 950 quạt máy.

b) Quan sát biểu đồ đoạn thẳng, ta thấy:

+ Cửa hàng bán được nhiều quạt máy nhất vào các tháng 6; 5; 8 với số lượng quạt máy bán được lần lượt là 150; 140; 140 (quạt máy).

+ Cửa hàng bán được ít quạt máy nhất vào các tháng 12; 1; 3 với số lượng quạt máy bán được lần lượt là 20; 25; 30 (quạt máy).

c) Trong 3 tháng mùa hè (tháng 4; 5; 6), cửa hàng bán được số quạt máy lần lượt là 120; 140; 150.

Tổng số quạt máy cửa hàng bán được trong ba tháng này là:

120 + 140 + 150 = 410 (quạt máy).

Tổng số quạt máy cửa hàng bán được trong ba tháng cửa hàng bán đắt nhất (tháng 5; 6; 8) là:

150 + 140 + 140 = 430 (quạt máy).

Vì 410 ≈ 430 nên ta có:

Số lượng quạt máy cửa hàng bán được trong 3 tháng mùa hè xấp xỉ ba tháng cửa hàng bán đắt nhất.

Vậy bạn Cường đã kết luận đúng.

Bài 4. Biểu đồ dưới đây cho biết thể loại sách, truyện mà 200 bạn học sinh khối 7 yêu thích nhất:

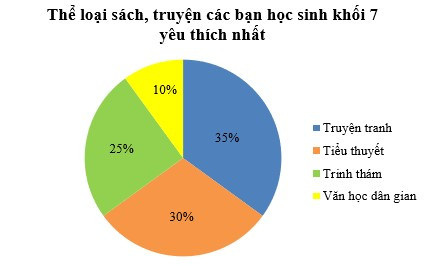
a) Thể loại nào chiếm tỉ lệ cao nhất? Có bao nhiêu bạn yêu thích thể loại đó?

b) Thể loại nào chiếm tỉ lệ thấp nhất? Có bao nhiêu bạn yêu thích thể loại đó?

c) Số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian bao nhiêu bạn?

Hướng dẫn giải

a) Thể loại truyện tranh chiếm tỉ lệ cao nhất với 35% so với cả bốn thể loại.

Số bạn yêu thích thể loại truyện tranh là: $\frac{200.35}{100}=70$ (bạn).

Vậy thể loại truyện tranh chiếm tỉ lệ cao nhất và có 70 bạn yêu thích thể loại truyện tranh.

b) Thể loại văn học dân gian chiếm tỉ lệ thấp nhất với 10% so với cả bốn thể loại.

Số bạn yêu thích thể loại văn học dân gian là: $\frac{200.10}{100}=20$ (bạn).

Vậy thể loại văn học dân gian chiếm tỉ lệ thấp nhất và có 20 bạn yêu thích thể loại văn học dân gian.

c) Số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian là: 70 – 20 = 50 (bạn).

Vậy số bạn thích truyện tranh nhiều hơn số bạn thích văn học dân gian là 50 bạn.

Bài 5. Biểu đồ sau đây thể hiện cơ cấu GDP của các ngành dịch vụ ở thành phố Hồ Chí Minh năm 2016 (đơn vị: %):

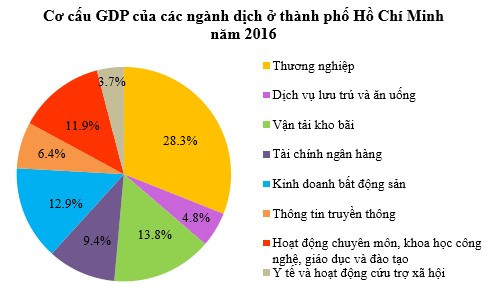
a) Trong dịch vụ tiêu dùng (Thương nghiệp; Dịch vụ lưu trú và ăn uống), ngành dịch vụ nào chiếm tỉ lệ cao nhất?

b) Tổng tỉ lệ dịch vụ sản xuất (Vận tải kho bãi; Tài chính ngân hàng; Kinh doanh bất động sản) gấp khoảng bao nhiêu lần so với tổng tỉ lệ dịch vụ công cộng (Thông tin truyền thông; Hoạt động chuyên môn, khoa học công nghệ, giáo dục và đào tạo; Y tế và hoạt động cứu trợ xã hội) (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

a) Quan sát biểu đồ, ta có 28,3% > 4,8%.

Vậy trong dịch vụ tiêu dùng, ngành dịch vụ chiếm tỉ lệ cao nhất là Thương nghiệp.

b) Tổng tỉ lệ dịch vụ sản xuất là: 13,8% + 9,4% + 12,9% = 36,1%.

Tổng tỉ lệ dịch vụ công cộng là: 6,4% + 11,9% + 3,7% = 22%.

Tổng tỉ lệ dịch vụ sản xuất gấp số lần so với tổng tỉ lệ dịch vụ công cộng là khoảng:

36,1% : 22% ≈ 1,6.

Vậy tổng tỉ lệ dịch vụ sản xuất gấp khoảng 1,6 lần so với tổng tỉ lệ dịch vụ công cộng.

Bài 6. Một hộp gồm có 30 chiếc thẻ, mỗi chiếc thẻ được ghi một trong các số 1; 2; 3; 4; 5; 6; ...; 29; 30. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Viết tập hợp X gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Xét biến cố “Số xuất hiện trên thẻ được rút ra là bội của 5”. Viết tập hợp Y gồm các kết quả có thể xảy ra và nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Số xuất hiện trên thẻ được rút ra là ước chung của 24 và 28”. Viết tập hợp Z gồm các kết quả có thể xảy ra và nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là:

X = {1; 2; 3; 4; 5; 6; ...; 29; 30}.

b) Ta có B(5) = {5; 10; 15; 20; 25; 30}.

Vậy tập hợp Y gồm các kết quả xảy ra đối với biến cố trên là:

Y = {5; 10; 15; 20; 25; 30} (lấy ra từ tập hợp X).

Có sáu kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là bội của 5” là: 5; 10; 15; 20; 25; 30 (lấy ra từ tập hợp X).

c) Ta có:

+) Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.

+) Ư(28) = {1; 2; 4; 7; 14; 28}.

Do đó ƯC(24; 28) = {1; 2; 4}.

Vậy tập hợp Z gồm các kết quả xảy ra đối với biến cố trên là:

Z = {1; 2; 4} (lấy ra từ tập hợp X).

Có ba kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là ước chung của 24 và 28” là: 1; 2; 4 (lấy ra từ tập hợp X).

Bài 7. Trên giá sách có 10 quyển sách khác nhau: Doraemon, Conan, Cổ tích, Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt. Chọn ngẫu nhiên một quyển sách trên giá sách.

a) Xét biến cố “Quyển sách được chọn là truyện tranh”. Nêu những kết quả thuận lợi cho biến cố đó.

b) Xét biến cố “Quyển sách được chọn là sách liên quan đến ngoại ngữ”. Nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Quyển sách được chọn là sách giáo khoa và liên quan đến văn học dân gian”. Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Thể loại truyện tranh gồm có các quyển: Doraemon, Conan.

Vậy có hai kết quả thuận lợi cho biến cố “Quyển sách được chọn là truyện tranh” là Doraemon và Conan.

b) Các sách liên quan đến ngoại ngữ là: Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt.

Vậy có ba kết quả thuận lợi cho biến cố “Quyển sách được chọn là sách liên quan đến ngoại ngữ” là Tiếng Anh, Từ điển Anh – Việt, Từ điển Pháp – Việt.

c) Thể loại sách giáo khoa gồm có các quyển: Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh.

Quyển sách liên quan đến văn học dân gian là: Cổ tích.

Vậy có sáu kết quả thuận lợi cho biến cố “Quyển sách được chọn là sách giáo khoa và liên quan đến văn học dân gian” là Ngữ văn, Toán, Lịch sử, Khoa học tự nhiên, Tiếng Anh, Cổ tích.

Bài 8. Một hộp chứa 20 viên bi gồm 8 viên bi đỏ, 5 viên bi vàng và 7 viên bi xanh. Mỗi viên bi đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8, mỗi viên bi vàng được ghi một trong các số 9; 10; 11; 12; 13, mỗi viên bi xanh được ghi một trong các số 14; 15; 16; 17; 18; 19; 20. Hai viên bi khác nhau được ghi hai số khác nhau. Lấy ra ngẫu nhiên một viên bi trong hộp đó.

a) Viết tập hợp D gồm các kết quả có thể xảy ra đối với viên bi được lấy ra.

b) Xét biến cố “Viên bi được lấy ra có màu vàng”. Nêu những kết quả thuận lợi cho biến cố đó.

c) Xét biến cố “Viên bi được lấy ra có màu đỏ hoặc xanh”. Nêu những kết quả thuận lợi cho biến cố đó.

d) Xét biến cố “Viên bi được lấy ra có màu đỏ hoặc vàng và số ghi trên viên bi là một số chia hết cho 2”. Nêu những kết quả thuận lợi cho biến cố đó.

Hướng dẫn giải

a) Tập hợp D gồm các kết quả có thể xảy ra đối với viên bi được lấy ra là:

D = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20}.

b) Trong 20 viên bi, viên bi có màu vàng được ghi một trong các số 9; 10; 11; 12; 13.

Vậy có năm kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu vàng” là: 9; 10; 11; 12; 13.

c) Trong 20 viên bi, ta có:

+) Viên bi có màu đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8.

+) Viên bi có màu xanh được ghi một trong các số 14; 15; 16; 17; 18; 19; 20.

Vậy có 15 kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu đỏ hoặc xanh” là: 1; 2; 3; 4; 5; 6; 7; 8; 14; 15; 16; 17; 18; 19; 20.

d) Ta có:

+) Viên bi có màu đỏ được ghi một trong các số 1; 2; 3; 4; 5; 6; 7; 8.

+) Viên bi có màu vàng được ghi một trong các số 9; 10; 11; 12; 13.

+) Các số chia hết cho 2 trong các số trên là: 2; 4; 6; 8; 10; 12.

Vậy có sáu kết quả thuận lợi cho biến cố “Viên bi được lấy ra có màu đỏ hoặc vàng và số ghi trên viên bi là một số chia hết cho 2” là: 2; 4; 6; 8; 10; 12.

Bài 9. Một hộp có 40 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 39; 40. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Tìm số phần tử của tập hợp H gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.

b) Tính xác suất của biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7”.

c) Tính xác suất của biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3”.

Hướng dẫn giải

a) Tập hợp gồm các kết quả có thể xảy ra đối với số trên thẻ được rút ra là:

H = {1; 2; 3; 4; ...; 39; 40}.

Vậy số phần tử của tập hợp H là 40.

b) Trong các số 1; 2; 3; 4; ...; 39; 40, các số có chữ số tận cùng là 7 là: 7; 17; 27; 37.

Do đó có bốn kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7” là 7; 17; 27; 37.

Xác suất của biến cố đó là: $\frac{4}{40}=\frac{1}{10}$.

Vậy xác suất của biến cố “Số trên thẻ được rút ra là số có chữ số tận cùng là 7” là $\frac{1}{10}$.

c) Trong các số 1; 2; 3; ...; 39; 40, các số chia hết cho 2 là: 2; 4; 6; 8; 10; 12; 14; 16; ...; 38; 40.

Trong các số 1; 2; 3; ...; 39; 40, các số chia hết cho 3 là: 3; 6; 9; 12; 15; 18; ...; 33; 36; 39.

Do đó trong các số được nêu ở trên, các số chia hết cho cả 2 và 3 là 6; 12; 18; 24; 30; 36.

Khi đó ta có sáu kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3” là 6; 12; 18; 24; 30; 36.

Xác suất của biến cố đó là: $\frac{6}{40}=\frac{3}{20}$.

Vậy xác suất của biến cố “Số trên thẻ được rút ra là số chia hết cho cả 2 và 3” là $\frac{3}{20}$.

B.2 Bài tập trắc nghiệm 

Câu 1. Trong cuộc khảo sát tìm hiểu về cách học của học sinh lớp 7B được kết quả như sau:

Có 20 học sinh học qua đọc, viết;

Có 10 học sinh trong lớp học qua nghe;

Có 10 học sinh trong lớp học qua vận động;

Có 5 học sinh học qua quan sát.

Khẳng định nào sau đây là đúng?

A. Kết quả trên là thu thập không có số liệu.

B. Kết quả trên là thu thập không phải là số.

C. Kết quả trên gồm cả dữ liệu là số liệu và dữ liệu không phải là số.

D. Kết quả trên là dữ liệu phần trăm không phải dữ liệu là số.

Hướng dẫn giải

Đáp án đúng là: C

Các hình thức học: đọc viết; nghe; vận động; quan sát. Đây là dữ liệu không phải là số.

Số lượng học sinh có cách học qua đọc, viết; nghe; vận động; quan sát lần lượt là: 20, 10, 10, 5. Dữ liệu này là số liệu.

Câu 2. Cho bảng thống kê lượng mưa tại trạm khí tượng Hà Nội trong sáu tháng cuối năm 2017.

Tháng	7	8	9	10	11	12
Lượng mưa (mm)	449,1	283,2	266,9	259,7	19,4	47,5

Trong các tháng trên, tháng nào có lượng mưa nhiều nhất?

A. Tháng 7;

B. Tháng 8;

C. Tháng 9;

D. Tháng 10.

Hướng dẫn giải

Đáp án đúng là: A

Tháng 7 có lượng mưa là 449,1 mm. Đây là tháng có lượng mưa nhiều nhất trong các tháng trên.

Câu 3. Biểu đồ dưới đây cho biết kỉ lục thế giới về thời gian chạy cự li 100 m trong các năm từ 1912 đến 2005:

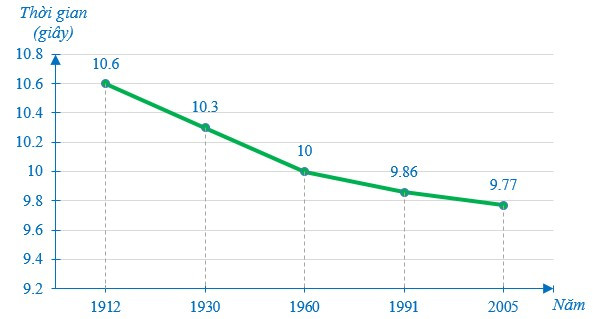
Từ năm 1912 đến 2005, kỉ lục thế giới về chạy cự li 100 m đã giảm được bao nhiêu giây?

A. 0,81 giây;

B. 0,83 giây;

C. 0,85 giây;

D. 0,87 giây.

Hướng dẫn giải

Đáp án đúng là: B

Kỉ lục chạy 100 m năm 1912 là 10,6 giây; năm 2005 là 9,77 giây.

Từ năm 1912 đến 2005, kỉ lục thế giới về chạy cự li 100 m đã giảm được:

10,6 – 9,77 = 0,83 giây

Câu 4. Tỉ lệ phần trăm các loại trái cây được giao cho cửa hàng A được biểu diễn bằng biểu đồ:

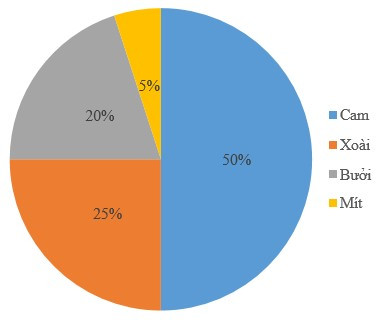
Số lượng cam được giao gấp bao nhiêu lần số lượng mít?

A. 5 lần;

B. 10 lần;

C. 15 lần;

D. 20 lần.

Hướng dẫn giải

Đáp án đúng là: B

Số lượng cam được giao chiếm 50%;

Số lượng mít được giao chiếm 5%;

Do 50% : 5% = 10.

Vậy nên số lượng cam được giao gấp 10 lần số lượng mít.

Câu 5. Cho biểu đồ biểu diễn thời gian chờ xe bus của Sơn. Tính xác suất của biến cố “Sơn phải chờ xe dưới 10 phút”.

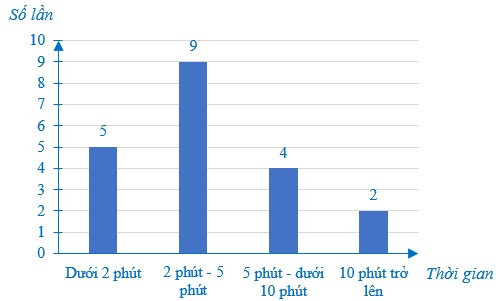
A. 0,1;

B. 0,2;

C. 0,9;

D. 0,5.

Hướng dẫn giải

Đáp án đúng là: C

Tổng số lần chờ xe bus của Sơn là: 5 + 9 + 4 + 2 = 20.

Số lần Sơn chờ xe dưới 10 phút là: 5 + 9 + 4 = 18.

Xác suất của biến cố “Sơn phải chờ xe dưới 10 phút” là: $\frac{18}{20}=0,9$.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Lý thuyết Toán 7 Chương 5: Một số yếu tố thống kê và xác suất

Lý thuyết Bài 1: Biểu thức số. Biểu thức đại số

Lý thuyết Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

Lý thuyết Bài 3: Phép cộng, phép trừ đa thức một biến