Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 3: Biểu đồ đoạn thẳng chi tiết sách Toán 7 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 3: Biểu đồ đoạn thẳng 

A. Câu hỏi trong bài

Giải Toán 7 trang 14 Tập 2

Câu hỏi khởi động trang 14 Toán 7 Tập 2: Biểu đồ ở Hình 11 biểu diễn thu nhập bình quân đầu người/ năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong giai đoạn từ năm 1986 đến năm 2020.

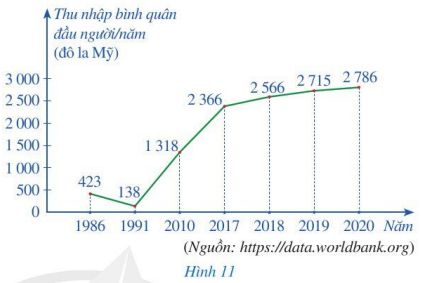
Biểu đồ ở Hình 11 là loại biểu đồ gì?

Lời giải:

Biểu đồ ở Hình 11 là biểu đồ đoạn thẳng, biểu diễn thu thập bình quân đầu người/ năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong giai đoạn từ năm 1986 đến năm 2020.

Hoạt động 1 trang 14 Toán 7 Tập 2: Quan sát biểu đồ thống kê ở Hình 11 và cho biết:

a) Đối tượng thống kê là gì và được biểu diễn trên trục nào?

b) Tiêu chí thống kê là gì và được biểu diễn trên trục nào?

c) Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định như thế nào?

Lời giải:

a) Đối tượng thống kê là các năm trong giai đoạn từ năm 1986 đến năm 2020: năm 1986, năm 1991, năm 2010, năm 2017, năm 2018, năm 2019, năm 2020. Đối tượng thống kê được biểu diễn trên trục nằm ngang.

b) Tiêu chí thống kê là thu nhập bình quân đầu người/ năm của Việt Nam (tính theo đô la Mỹ) trong những năm nêu trên. Tiêu chí thống kê được biểu diễn trên trục thẳng đứng.

c) Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi năm thống kê và thu nhập bình quân đầu người/ năm của Việt Nam trong năm đó.

Giải Toán 7 trang 16 Tập 2

Hoạt động 2 trang 16 Toán 7 Tập 2: Nêu một số dạng biểu diễn của một tập dữ liệu.

Lời giải:

Dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau như: biểu đồ tranh, biểu đồ cột, biểu đồ cột kép, biểu đồ đoạn thẳng.

Hoạt động 3 trang 17 Toán 7 Tập 2: Biểu đồ đoạn thẳng trong Hình 17 biểu diễn nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm.

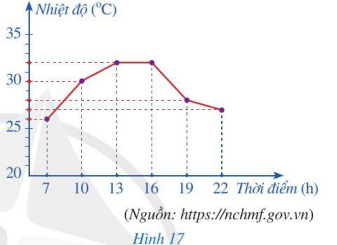
a) Nêu nhiệt độ lúc 7 h, 10 h, 13 h, 16 h, 19 h, 22 h.

b) Hãy nhận xét về sự thay đổi nhiệt độ trong các khoảng thời gian: 7 h – 10 h (tức là từ 7 h đến 10 h); 10 h – 13 h ; 13 h – 16 h; 16 h – 19 h; 19 h – 22 h.

Lời giải:

a) Quan sát biểu đồ Hình 17, ta thấy ở Hà Nội trong ngày 07/05/2021 thì:

- Nhiệt độ lúc 7 h là: 26°C;

- Nhiệt độ lúc 10 h là: 30°C;

- Nhiệt độ lúc 13 h là: 32°C;

- Nhiệt độ lúc 16 h là: 32°C;

- Nhiệt độ lúc 19 h là: 28°C;

- Nhiệt độ lúc 22 h là: 27°C.

b) Sự thay đổi về nhiệt độ trong các khoảng thời gian:

+) 7 h – 10 h: nhiệt độ tăng từ 26°C lên 30°C;

+) 10 h – 13 h: nhiệt độ tăng từ 30°C lên 32°C;

+) 13 h – 16 h: nhiệt độ ổn định ở 32°C;

+) 16 h – 19 h: nhiệt độ giảm từ 32°C xuống 28°C;

+) 19 h – 22 h: nhiệt độ giảm từ 28°C xuống 27°C.

Vậy, nhiệt độ tăng trong các khoảng thời gian: 7 h – 10 h và 10 h – 13 h;

Nhiệt độ ổn định trong khoảng thời gian: 13 h – 16 h;

Nhiệt độ giảm trong các khoảng thời gian: 16 h – 19 h và 19 h – 22 h.

B. Bài tập

Giải Toán 7 trang 19 Tập 2

Bài 1 trang 19 Toán 7 Tập 2: Biểu đồ đoạn thẳng trong Hình 19 biểu diễn nhiệt độ trong một ngày mùa đông tại một địa điểm ở miền ôn đới.

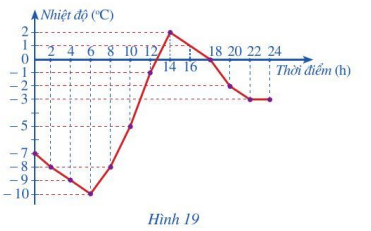
a) Nêu nhiệt độ lúc 2 h, 6 h, 10 h, 14 h, 18 h, 22 h.

b) Hãy nhận xét về sự thay đổi nhiệt độ trong các khảng thời gian 2 h – 6 h; 6 h – 10 h; 10 h – 14 h; 14 h – 18 h; 18 h – 22 h; 22 h – 24 h.

Lời giải:

a) Quan sát biểu đồ Hình 19, ta thấy trong một ngày mùa đông tại địa điểm ở miền ôn đới đó có:

- Nhiệt độ lúc 2 h là: ‒8°C;

- Nhiệt độ lúc 6 h là: ‒10°C;

- Nhiệt độ lúc 10 h là: ‒5°C;

- Nhiệt độ lúc 14 h là: 2°C;

- Nhiệt độ lúc 18 h là: 0°C;

- Nhiệt độ lúc 22 h là: ‒3°C.

b) Sự thay đổi về nhiệt độ trong các khoảng thời gian:

+) 2 h – 6 h: nhiệt độ giảm từ ‒8°C xuống ‒10°C;

+) 6 h – 10 h: nhiệt độ tăng từ ‒10°C lên ‒5°C;

+) 10 h – 14 h: nhiệt độ tăng từ ‒5°C lên 2°C;

+) 14 h – 18 h: nhiệt độ giảm từ 2°C xuống 0°C;

+) 18 h – 22 h: nhiệt độ giảm từ 0°C xuống ‒3°C.

+) 22 h – 24 h: nhiệt độ ổn định ở ‒3°C.

Vậy, nhiệt độ giảm trong các khoảng thời gian: 2 h – 6 h; 14 h – 18 h và 14 h – 18 h;

Nhiệt độ tăng trong các khoảng thời gian: 6 h – 10 h và 10 h – 14 h;

Nhiệt độ ổn định trong khoảng thời gian: 22 h – 24 h.

Bài 2 trang 19 Toán 7 Tập 2: Biểu đồ đoạn thẳng ở Hình 20 biểu diễn lượng mưa trung bình tháng ở Cần Thơ.

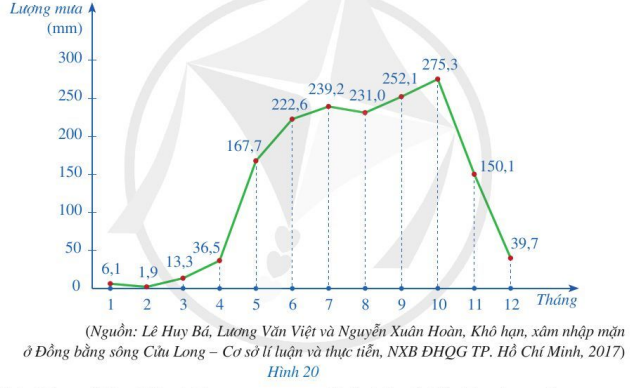
a) Lập bảng số liệu thống kê lượng mưa trung bình năm ở Cần Thơ.

b) Tính tổng lượng mưa trung bình năm ở Cần Thơ.

c) Tìm ba tháng có lượng mưa trung bình tháng lớn nhất ở Cần Thơ.

d) Tìm ba tháng khô hạn nhất ở Cần Thơ.

Lời giải:

a) Quan sát biểu đồ Hình 20, ta thấy:

- Lượng mưa trung bình tháng 1 là: 6,1 mm;

- Lượng mưa trung bình tháng 2 là: 1,9 mm;

Tương tự với các tháng còn lại, ta có bảng sau:

b) Tổng lượng mưa trung bình năm ở Cần Thơ là:

6,1 + 1,9 + 13, 3 + 36,5 + 167,7 + 222,6 + 239,2 + 231,0 + 252,1 + 275,3 + 150,1 + 39,7 = 1635,5 (mm)

c) Ba tháng có lượng mưa trung bình tháng lớn nhất ở Cần Thơ là: tháng 7 (239,2 mm), tháng 9 (252,1 mm) và tháng 10 (275,3 mm).

d) Ba tháng khô hạn nhất ở Cần Thơ là: tháng 1 (6,1 mm), tháng 2 (1,9 mm), tháng 3 (13,3

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 2: Phân tích và xử lí dữ liệu 

Giải SGK Toán 7 Bài 3: Biểu đồ đoạn thẳng 

Giải SGK Toán 7 Bài 4: Biểu đồ hình quạt tròn 

Giải SGK Toán 7 Bài 5: Biến cố trong một số trò chơi đơn giản 

Giải SGK Toán 7 Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Lý thuyết Biểu đồ đoạn thẳng

1. Biểu đồ đoạn thẳng

Biểu đồ đoạn thẳng có các yếu tố sau:

+ Trục nằm ngang biểu diễn các đối tượng thống kê;

+ Trục thẳng đứng biểu diễn tiêu chí thống kê và trên trục đó đã xác định độ dài đơn vị thống kê;

+ Biểu đồ đoạn thẳng là đường gấp khúc nối từng điểm liên tiếp bằng các đoạn thẳng;

+ Mỗi điểm đầu mút của các đoạn thẳng trong đường gấp khúc được xác định bởi một đối tượng thống kê và số liệu thống kê theo tiêu chí của đối tượng đó.

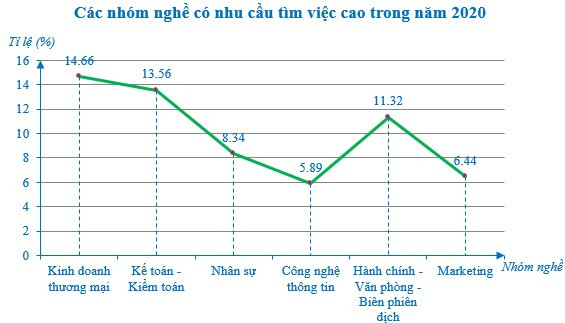
Ví dụ: Cho biểu đồ đoạn thẳng sau thể hiện các nhóm nghề có nhu cầu tìm việc cao tại Thành phố Hồ Chí Minh trong năm 2020 (đơn vị: %):

Ở biểu đồ trên, ta có:

+ Trục nằm ngang biểu diễn các đối tượng thống kê là các nhóm nghề bao gồm: Kinh doanh thương mại; Kế toán – Kiểm toán; Nhân sự; Công nghệ thông tin; Hành chính – Văn phòng – Biên phiên dịch; Marketing;

+ Trục thẳng đứng biểu diễn tiêu chí thống kê là tỉ lệ (tính theo %) nhu cầu tìm việc của các nhóm nghề nêu trên;

+ Đường gấp khúc gồm các đoạn thẳng nối liền liên tiếp 6 điểm. Mỗi điểm được xác định bởi nhóm nghề và tỉ lệ nhu cầu tìm việc của nhóm nghề đó.

Ví dụ: Biểu đồ sau đây cho biết số cung thủ bắn trúng tâm đỏ trong năm lần bắn liên tiếp.

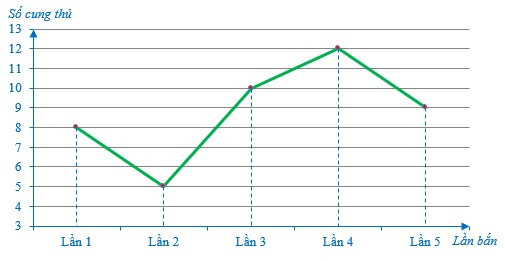
Nêu số cung thủ bắn trúng tâm đỏ trong từng lần bắn của các cung thủ.

Hướng dẫn giải

Để biết số cung thủ bắn trúng tâm đỏ trong từng lần bắn, ta làm như sau:

+ Từ điểm “Lần 1” trên trục nằm ngang, dóng theo chiều thẳng đứng tới đầu mút của đoạn thẳng thuộc đường gấp khúc;

+ Đi tiếp theo chiều ngang về bên trái cho đến khi gặp trục thẳng đứng;

+ Đọc chỉ số trên trục thẳng đứng.

Ta có: Số cung thủ bắn trúng tâm đỏ trong lần 1 là 8 (cung thủ).

Tương tự như trên, số cung thủ bắn trúng tâm đỏ trong lần 2, lần 3, lần 4, lần 5 lần lượt là: 5; 10; 12; 9 (cung thủ).

Vậy số cung thủ bắn trúng tâm đỏ trong lần 1, lần 2, lần 3, lần 4, lần 5 lần lượt là 8; 5; 10; 12; 9 (cung thủ).

Chú ý:

+ Cũng như biểu đồ cột và biểu đồ cột kép, biểu đồ đoạn thẳng giúp chúng ta “trực quan hóa” một tập dữ liệu thống kê thông qua cách biểu diễn hình học tập dữ liệu đó.

+ Người ta còn biểu diễn dữ liệu thống kê ở dạng biểu đồ tương tự biểu đồ cột, trong đó các cột được thay bằng các đoạn thẳng. Biểu đồ đó cũng gọi là biểu đồ đoạn thẳng.

Chẳng hạn như biểu đồ dưới đây:

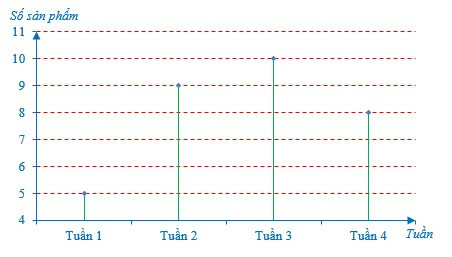
Ví dụ: Để theo dõi lượng táo mà đội hái trái cây hái được mỗi ngày trong một tuần, người chủ nông trại đã kiểm đếm (tính theo đơn vị kg) mỗi ngày và ghi lại như bảng sau:

Chọn số liệu thích hợp để điền vào dấu “?” trong biểu đồ sau:

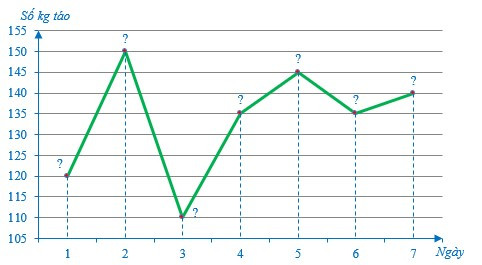
Hướng dẫn giải

Sau khi hoàn thiện các số liệu vào biểu đồ, ta nhận được biểu đồ sau biểu diễn số kg táo đội hái trái cây hái được trong một tuần mà chủ nông trại kiểm đếm:

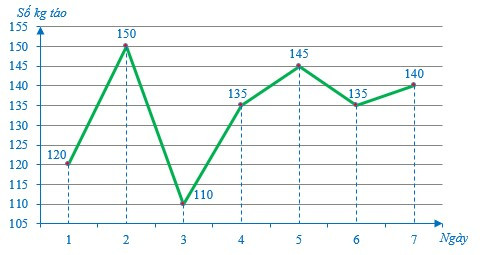
Nhận xét: Như ta đã biết, dữ liệu thống kê có thể biểu diễn ở những dạng khác nhau, trong đó có biểu đồ đoạn thẳng.

Ví dụ: Biểu đồ sau đây thể hiện lượng gạo Việt Nam xuất khẩu trong 6 tháng đầu năm 2019:

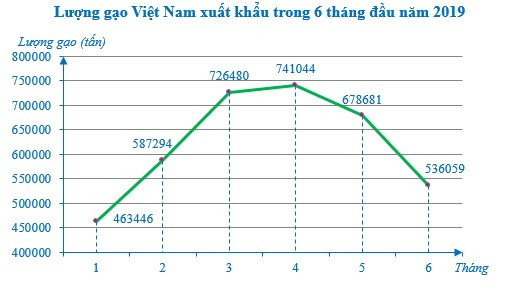
Lập bảng số liệu thống kê lượng gạo Việt Nam xuất khẩu năm 2019.

Hướng dẫn giải

Từ biểu đồ trên, ta có bảng số liệu sau:

2. Phân tích và xử lí dữ liệu biểu diễn bằng biểu đồ đoạn thẳng

Dựa vào biểu đồ đoạn thẳng, ta có thể xác định xu hướng tăng hoặc giảm của tập số liệu trong một khoảng thời gian nhất định.

Ví dụ: Một cửa hàng bán điện thoại smartphone đã thống kê lại số lượng điện thoại smartphone bán được mỗi tuần của tháng 2 năm 2021 như biểu đồ bên dưới.

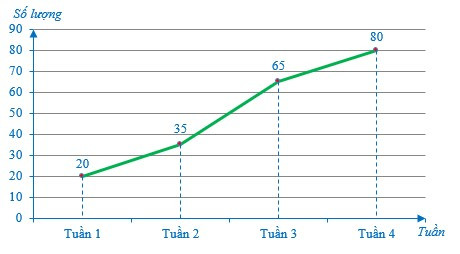
a) Lập bảng số liệu thống kê số lượng điện thoại smartphone cửa hàng đã bán được mỗi tuần của tháng 2 năm 2021.

b) Trong 4 tuần đó, tuần nào cửa hàng bán được nhiều điện thoại nhất?

c) Số lượng điện thoại bán được ở tuần 3 tăng bao nhiêu phần trăm so với tuần 2 (làm tròn kết quả đến hàng phần trăm)?

d) Dựa vào biểu đồ đoạn thẳng, nêu nhận xét về số lượng điện thoại smartphone cửa hàng đã bán được trong tháng 2 năm 2021.

Hướng dẫn giải

a) Từ biểu đồ trên, ta có bảng số liệu sau:

b) Trong 4 tuần đó, tuần 4 cửa hàng bán được nhiều điện thoại nhất với số lượng điện thoại smartphone bán được là 80 điện thoại.

c) Tỉ số phần trăm của số lượng điện thoại bán được ở tuần 3 và số lượng điện thoại bán được ở tuần 2 là:

$\frac{65.100}{35}\%\approx 185,71\%$.

Vậy số lượng điện thoại bán được ở tuần 3 đã tăng 185,71% – 100% = 85,71% so với tuần 2.

d) Dựa vào biểu đồ đoạn thẳng, ta thấy số lượng điện thoại cửa hàng bán được liên tục tăng trong tháng 2 năm 2021.