Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 7: Phép nhân các phân thức đại số, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phép nhân các phân thức đại số lớp 8.

Giải bài tập Toán lớp 8 Bài 7: Phép nhân các phân thức đại số

Trả lời các câu hỏi giữa bài

Trả lời câu hỏi 1 trang 51 sgk Toán 8 Tập 1: Cho hai phân thức: ${\displaystyle \frac{3x^2}{x+5}}$ và ${\displaystyle \frac{x^2-25}{6x^3}}$. Cũng làm như nhân hai phân số, hãy nhân tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức.

Phương pháp giải: Quy tắc nhân hai phân số.

Lời giải:

$\begin{array}{rl}& \frac{3x^2}{x+5}.\frac{x^2-25}{6x^3}=\frac{3x^2.\left(x^2-25\right)}{\left(x+5\right).6x^3}\\ & =\frac{3x^2\left(x+5\right)\left(x-5\right)}{\left(x+5\right).6x^3}=\frac{x-5}{2x}\end{array}$

Trả lời câu hỏi 2 trang 52 sgk Toán 8 Tập 1: Làm tính nhân phân thức: ${\displaystyle \frac{{\left(x-13\right)}^2}{2x^5}}.\left(-{\displaystyle \frac{3x^2}{x-13}}\right)$

Phương pháp giải: Muốn nhân hai phân thức ta nhân các tử thức với nhau, các mẫu thức với nhau rồi rút gọn phân thức vừa tìm được: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$

Lời giải:

$\begin{array}{rl}& \frac{{\left(x-13\right)}^2}{2x^5}.\left(-\frac{3x^2}{x-13}\right)\\ & =\frac{{\left(x-13\right)}^2.\left(-3x^2\right)}{2x^5(x-13)}=\frac{-3\left(x-13\right)}{2x^3}\end{array}$

Trả lời câu hỏi 3 trang 52 sgk Toán 8 Tập 1: Thực hiện phép tính: ${\displaystyle \frac{x^2+6x+9}{1-x}}.{\displaystyle \frac{{\left(x-1\right)}^3}{2{\left(x+3\right)}^3}}$

Phương pháp giải: Muốn nhân hai phân thức ta nhân các tử thức với nhau, các mẫu thức với nhau rồi rút gọn phân thức vừa tìm được: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$

Lời giải:

$\begin{array}{rl}& \frac{x^2+6x+9}{1-x}.\frac{{\left(x-1\right)}^3}{2{\left(x+3\right)}^3}\\ & =\frac{\left(x^2+6x+9\right).{\left(x-1\right)}^3}{\left(1-x\right).2{\left(x+3\right)}^3}\\ & =\frac{\left(x^2+2.x.3+3^2\right).{\left(x-1\right)}^3}{-2\left(x-1\right){\left(x+3\right)}^3}\\ & =\frac{{\left(x+3\right)}^2{\left(x-1\right)}^3}{-2\left(x-1\right){\left(x+3\right)}^3}\\ & =\frac{-{\left(x-1\right)}^2}{2\left(x+3\right)}\end{array}$

Trả lời câu hỏi 4 trang 52 sgk Toán 8 Tập 1: Tính nhanh: ${\displaystyle \frac{3x^5+5x^3+1}{x^4-7x^2+2}}.{\displaystyle \frac{x}{2x+3}}.{\displaystyle \frac{x^4-7x^2+2}{3x^5+5x^3+1}}$

Phương pháp giải: Muốn nhân hai phân thức ta nhân các tử thức với nhau, các mẫu thức với nhau rồi rút gọn phân thức vừa tìm được: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$

Lời giải:

$\begin{array}{rl}& \frac{3x^5+5x^3+1}{x^4-7x^2+2}.\frac{x}{2x+3}.\frac{x^4-7x^2+2}{3x^5+5x^3+1}\\ & =\frac{\left(3x^5+5x^3+1\right).x.\left(x^4-7x^2+2\right)}{\left(x^4-7x^2+2\right).\left(2x+3\right).\left(3x^5+5x^3+1\right)}\\ & =\frac{x}{2x+3}\end{array}$

Câu hỏi và bài tập (trang 52, 53 sgk Toán 8 Tập 1)

Bài 38 trang 52 sgk Toán 8 Tập 1: Thực hiện các phép tính sau:

a) ${\displaystyle \frac{15x}{7y^3}}.{\displaystyle \frac{2y^2}{x^2}}$;

b) ${\displaystyle \frac{4y^2}{11x^4}}.\left(-{\displaystyle \frac{3x^2}{8y}}\right)$;

c) ${\displaystyle \frac{x^3-8}{5x+20}}.{\displaystyle \frac{x^2+4x}{x^2+2x+4}}$

Phương pháp giải:  - Áp dụng quy tắc nhân hai phân thức: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$.

- Sau đó rút gọn phân thức.

Lời giải:

a) ${\displaystyle \frac{15x}{7y^3}}.{\displaystyle \frac{2y^2}{x^2}}={\displaystyle \frac{15x.2y^2}{7y^3.x^2}}$

    $={\displaystyle \frac{30x{y}^2}{7x^2{y}^3}}={\displaystyle \frac{30}{7xy}}$ 

b) ${\displaystyle \frac{4y^2}{11x^4}}.\left(-{\displaystyle \frac{3x^2}{8y}}\right)={\displaystyle \frac{4y^2.(-3x^2)}{11x^4.8y}}$

    $=-{\displaystyle \frac{3.4x^2{y}^2}{11.8x^{4}y}}=-{\displaystyle \frac{3y}{22x^2}}$

c) ${\displaystyle \frac{x^3-8}{5x+20}}.{\displaystyle \frac{x^2+4x}{x^2+2x+4}}$ 

    $={\displaystyle \frac{(x^3-8)(x^2+4x)}{5(x+4)(x^2+2x+4)}}$

    $={\displaystyle \frac{x(x-2)(x^2+2x+4)(x+4)}{5(x+4)(x^2+2x+4)}}$

    $={\displaystyle \frac{x(x-2)}{5}}$

Bài 39 trang 52 sgk Toán 8 Tập 1: Thực hiện các phép tính sau:

a) ${\displaystyle \frac{5x+10}{4x-8}}.{\displaystyle \frac{4-2x}{x+2}}$;

b) ${\displaystyle \frac{x^2-36}{2x+10}}.{\displaystyle \frac{3}{6-x}}$

Phương pháp giải:  - Áp dụng quy tắc nhân hai phân thức: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$.

Lời giải:

a) ${\displaystyle \frac{5x+10}{4x-8}}.{\displaystyle \frac{4-2x}{x+2}}$ 

$={\displaystyle \frac{(5x+10).(4-2x)}{(4x-8).(x+2)}}$

$={\displaystyle \frac{5(x+2).2(2-x)}{4(x-2)(x+2)}}$

$={\displaystyle \frac{5(2-x)}{2(x-2)}}={\displaystyle \frac{-5(x-2)}{2(x-2)}}=-{\displaystyle \frac{5}{2}}$

b) ${\displaystyle \frac{x^2-36}{2x+10}}.{\displaystyle \frac{3}{6-x}}$ 

$={\displaystyle \frac{(x^2-36).3}{(2x+10)(6-x)}}$

$={\displaystyle \frac{-3(36-x^2)}{(2x+10)(6-x)}}$

$={\displaystyle \frac{-3(6-x)(x+6)}{2(x+5)(6-x)}}$

$=-{\displaystyle \frac{3(x+6)}{2(x+5)}}$

Bài 40 trang 53 sgk Toán 8 Tập 1: Rút gọn biểu thức sau theo hai cách (sử dụng và không sử dụng tính chất phân phối của phép nhân đối với phép cộng): ${\displaystyle \frac{x-1}{x}}.\left(x^2+x+1+{\displaystyle \frac{x^3}{x-1}}\right)$

Phương pháp giải: - Áp dụng tính chất phân phối của phép nhân đối với phép cộng: ${\displaystyle \frac{A}{B}}.\left({\displaystyle \frac{C}{D}}+{\displaystyle \frac{G}{H}}\right)={\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}+{\displaystyle \frac{A}{B}}.{\displaystyle \frac{G}{H}}$

- Áp dụng quy tắc nhân hai phân thức: ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$

Lời giải:

Cách 1: Áp dụng tính phân phối:  

${\displaystyle \frac{x-1}{x}}.\left(x^2+x+1+{\displaystyle \frac{x^3}{x-1}}\right)$

$={\displaystyle \frac{x-1}{x}}.\left[\left(x^2+x+1\right)+{\displaystyle \frac{x^3}{x-1}}\right]$

$={\displaystyle \frac{x-1}{x}}.\left(x^2+x+1\right)+{\displaystyle \frac{x-1}{x}}.{\displaystyle \frac{x^3}{x-1}}$

$={\displaystyle \frac{(x-1)(x^2+x+1)}{x}}+{\displaystyle \frac{(x-1)x^3}{x(x-1)}}$

$={\displaystyle \frac{x^3-1}{x}}+{\displaystyle \frac{x^3}{x}}$

$={\displaystyle \frac{x^3-1+x^3}{x}}={\displaystyle \frac{2x^3-1}{x}}$

Cách 2: Không áp dụng tính phân phối:

${\displaystyle \frac{x-1}{x}}.\left(x^2+x+1+{\displaystyle \frac{x^3}{x-1}}\right)$

$={\displaystyle \frac{x-1}{x}}.\left({\displaystyle \frac{(x^2+x+1)(x-1)}{x-1}}+{\displaystyle \frac{x^3}{x-1}}\right)$

$={\displaystyle \frac{x-1}{x}}.\left({\displaystyle \frac{x^3-1}{x-1}}+{\displaystyle \frac{x^3}{x-1}}\right)$

$={\displaystyle \frac{x-1}{x}}.{\displaystyle \frac{x^3-1+x^3}{x-1}}$

$={\displaystyle \frac{(x-1)(2x^3-1)}{x(x-1)}}={\displaystyle \frac{2x^3-1}{x}}$

Bài 41 trang 53 sgk Toán 8 Tập 1: Đố. Đố em điền được vào chỗ trống của phép nhân dưới đây những phân thức có mẫu thức bằng tử thức cộng với 1

${\displaystyle \frac{1}{x}}.{\displaystyle \frac{x}{x+1}}....={\displaystyle \frac{1}{x+7}}$

Phương pháp giải: Áp dụng qui tắc: Mẫu số của phân số bên trái sẽ giản ước với tử số của phân số bên phải liền sau nó. Cứ làm như vậy cho đến khi mẫu số của phân số cuối cùng bằng với mẫu số của phân số kết quả. Trong bài này là $x+7$.

Lời giải:

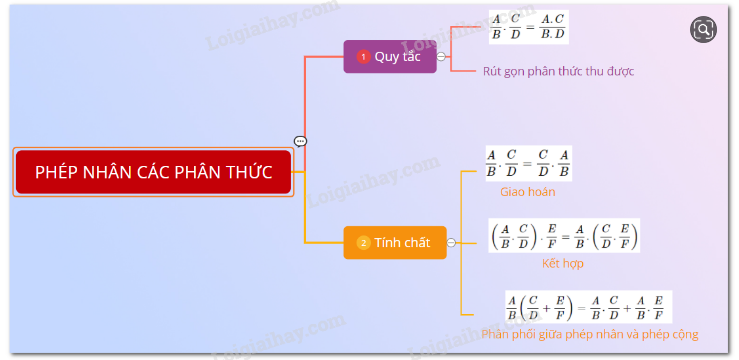
Lý thuyết phép nhân các phân thức đại số

1. Quy tắc: Muốn nhân hai phân thức ta nhân các tử thức với nhau, các mẫu thức với nhau rồi rút gọn phân thức vừa tìm được:

${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{A.C}{B.D}}$

Ví dụ: $\frac{2x}{x+2}.\frac{x+1}{x}=\frac{2x.(x+1)}{(x+2).x}=\frac{2.(x+1)}{x+2}$

2. Các tính chất:

a) Giao hoán ${\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}={\displaystyle \frac{C}{D}}.{\displaystyle \frac{A}{B}}$

b) Kết hợp $\left({\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}\right).{\displaystyle \frac{E}{F}}={\displaystyle \frac{A}{B}}.\left({\displaystyle \frac{C}{D}}.{\displaystyle \frac{E}{F}}\right)$

c) Phân phối đối với phép cộng ${\displaystyle \frac{A}{B}}\left({\displaystyle \frac{C}{D}}+{\displaystyle \frac{E}{F}}\right)={\displaystyle \frac{A}{B}}.{\displaystyle \frac{C}{D}}+{\displaystyle \frac{A}{B}}.{\displaystyle \frac{E}{F}}$