Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 2: Tính chất cơ bản của phân thức, chi tiết nhất giúp học sinh dễ dàng làm bài tập Tính chất cơ bản của phân thức lớp 8.
Giải bài tập Toán lớp 8 Bài 2: Tính chất cơ bản của phân thức
Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 37 sgk Toán 8 Tập 1: Hãy nhắc lại tính chất cơ bản của phân số.
Lời giải:
- Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác thì ta được một phân số bằng phân số đã cho.
với và
- Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
với
Phương pháp giải: Áp dụng quy tắc nhân đơn thức với đa thức.
Áp dụng định nghĩa hai phân thức bằng nhau.
Lời giải:
Nhân cả tử và mẫu của phân thức với ta được phân thức:
So sánh hai phân thức: và
Xét tích chéo:
Nên
Phương pháp giải: Áp dụng quy tắc nhân chia đơn thức với đơn thức, định nghĩa hai phân thức bằng nhau.
Lời giải:
Ta có:
Suy ra, chia cả tử và mẫu của phân thức cho ta được phân thức
So sánh hai phân thức: và
Xét tích chéo:
Suy ra:
Do đó:
Phương pháp giải: Áp dụng quy tắc chia đa thức cho đa thức.
Lời giải:
Phương pháp giải: Áp dụng:
Lời giải:
Vậy ta điền vào câu a và vào câu b.
Câu hỏi và bài tập (trang 38 sgk Toán 8 Tập 1)
a) ( Lan);
b) ( Hùng)
c) ( Giang);
d) ( Huy)
Em hãy dùng tính chất cơ bản của phân thức và qui tắc đổi dấu để giải thích ai viết đúng, ai viết sai. Nếu có chỗ nào sai em hãy sửa lại cho đúng.
Phương pháp giải: Áp dụng tính chất cơ bản của phân thức và quy tắc đổi dấu phân thức:
- Nếu nhân (hoặc chia) cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
- Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
Lời giải:
a) Lan viết đúng
b)
Hùng viết sai vì đã chia tử của vế trái cho nhân tử chung thì cũng phải chia mẫu của nó cho . Sửa lại là:
hoặc
c) Giang viết đúng
d)
Do đó:
Suy ra Huy viết sai.
Bài 5 trang 38 sgk Toán 8 Tập 1: Điền đa thức thích hợp vào mỗi chỗ trống trong các đẳng thức sau:
a) ;
b) .
Phương pháp giải: Áp dụng tính chất cơ bản của phân thức: Nếu nhân (hoặc chia) cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
Lời giải:
a)
Ta có:
Chia cả tử và mẫu cho , ta được:
Vậy phải điền vào chỗ trống.
b) .
Phân tích tử của phân thức ở vế phải ta được . Do đó đẳng thức đã cho có thể viết là:
Như vậy ta phải nhân cả tử và mẫu của phân thức ở vế trái với ta được:
Vậy đa thức phải điền vào chỗ trống là .
Phương pháp giải: Áp dụng tính chất cơ bản của phân thức và áp dụng hằng đẳng thức hiệu hai bình phương, phép chia đa thức một biến đã sắp xếp.
Lời giải:
Nên
Ta được
Suy ra
Vậy
Vậy ta phải thực hiện phép chia cho
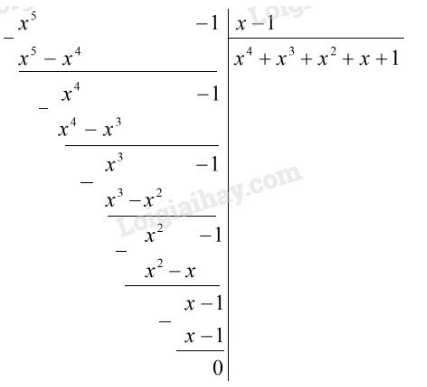
Vậy phải điền vào chỗ trống :
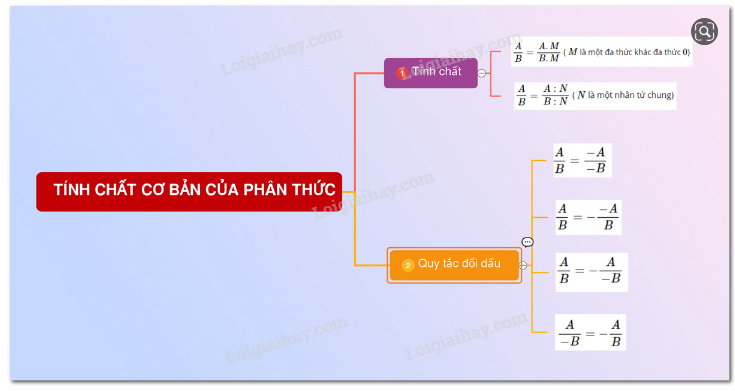
Lý thuyết tính chất cơ bản của phân thức
1. Tính chất cơ bản của phân thức: Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
( là một đa thức khác đa thức )
- Nếu chia cả tử và mẫu của một đa thức cho một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
( là một nhân tử chung)
Ví dụ:
2. Qui tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
Ví dụ: