Với giải Bài 55 trang 89 Toán lớp 9 chi tiết trong Bài 7: Tứ giác nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 7: Tứ giác nội tiếp

Bài 55 trang 89 SGK Toán lớp 9 Tập 2: Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết $\widehat{DAB}={80}^o, \widehat{DAM}={30}^o$, $\widehat{BMC}={70}^o.$

Hãy tính số đo các góc $\widehat{MAB},\widehat{BCM},\widehat{AMB},$$\widehat{DMC},\widehat{AMD},\widehat{MCD}$ và $\widehat{BCD}$.

Lời giải:

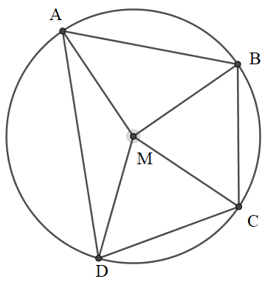
Ta có: $\widehat{MAB}=\widehat{DAB}-\widehat{DAM}$$={80}^o-{30}^o={50}^o$ (1)

Xét tam giác MBC có:

MB = MC (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MBC cân tại M

$\Rightarrow \widehat{BCM}=\widehat{CBM}=\frac{{180}^o-\widehat{BMC}}{2}$$=\frac{{180}^o-{70}^o}{2}={55}^o$

Xét tam giác MAB có:

MA = MB (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MAB cân tại M

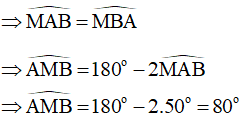
Ta có: Góc BAD là góc nội tiếp chắn cung BCD

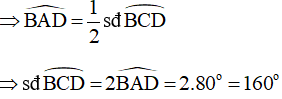
Mà ta có:

Góc BMC là góc ở tâm chắn cung nhỏ BC

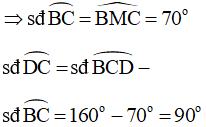
Mà góc DMC là góc ở tâm chắn cung nhỏ DC $\Rightarrow \widehat{DMC}={90}^o$

Xét tam giác MAD có:

MA = MD (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MAD cân tại M

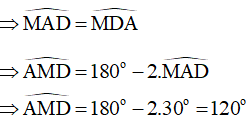
Xét tam giác MCD có:

MC = MD (cùng bằng bán kính đường tròn (O))

$\widehat{DMC}={90}^o$ (chứng minh trên)

Do đó, tam giác MCD vuông cân tại M

$\Rightarrow \widehat{MDC}=\widehat{MCD}={45}^o$

Ta lại có: CM là tia CM là tia nằm giữa hai tia CB, CD nên ta có:

$$\begin{gathered} \widehat{BCD}=\widehat{BCM}+\widehat{MCD} \\ ={55}^o+{45}^o={100}^o \end{gathered}$$