SBT Toán 9 Bài 7: Tứ giác nội tiếp

SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9

thuy an pham Ngày: 24-05-2022 Lớp 9

4.2 K

Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 7: Tứ giác nội tiếp chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 7: Tứ giác nội tiếp

Bài 39 trang 106 SBT Toán 9 tập 2: Trên đường tròn tâm

O

có một cung

A B

và

S

là điểm chính giữa của cung đó. Trên dây

A B

lấy hai điểm

E

và

H .

Các đường thẳng

S H

và

S E

cắt đường tròn theo thứ tự tại

C

và

D .

Chứng minh

E H C D

là một tứ giác nội tiếp.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Nếu $C$ là một điểm trên cung $A B$ thì: $s đ \overset{⏜}{A B} = s đ \overset{⏜}{A C} + s đ \overset{⏜}{C B} .$

+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng $180^{\circ}$ thì tứ giác đó nội tiếp được đường tròn.

Lời giải:

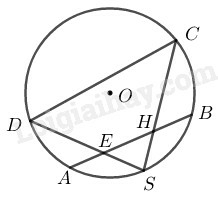
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 1)

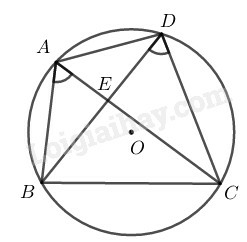
$S$ là điểm chính giữa của cung $\overset{⏜}{A B}$ .

$\Rightarrow$ $\overset{⏜}{S A} = \overset{⏜}{S B}$ $(1)$

$\hat{D E B} = \frac{1}{2} (s đ \overset{⏜}{D C B} + s đ \overset{⏜}{A S})$ (góc có đỉnh ở bên trong đường tròn) $(2)$

$\hat{D C S} = \frac{1}{2} s đ \overset{⏜}{D A S}$ (tính chất góc nội tiếp) hay $\hat{D C S} = \frac{1}{2} (s đ \overset{⏜}{D A} + s đ \overset{⏜}{S A}$ ) $(3)$

Từ $(1)$ và $(2)$ suy ra: $\hat{D E B} + \hat{D C S}$ $= \frac{1}{2} (s đ \overset{⏜}{D C B} + s đ \overset{⏜}{A S} + s đ \overset{⏜}{D A} + s đ \overset{⏜}{S A})$ $(4)$

Từ $(1)$ và $(4)$ suy ra: $\hat{D E B} + \hat{D C S}$ $= \frac{1}{2} (s đ \overset{⏜}{D C B} + s đ \overset{⏜}{B S} + s đ \overset{⏜}{S A} + s đ \overset{⏜}{D A})$ $= \frac{360^{\circ}}{2} = 180^{\circ}$

Hay $\hat{D E H} + \hat{D C H} = 180^{\circ}$

Vậy: tứ giác $E H C D$ nội tiếp được trong một đường tròn.

Bài 40 trang 106 SBT Toán 9 tập 2: Cho tam giác

A B C .

Các đường phân giác trong của

\hat{B}

và

\hat{C}

cắt nhau tại

S,

các đường phân giác ngoài của

\hat{B}

và

\hat{C}

cắt nhau tại

E .

Chứng minh

B S C E

là một tứ giác nội tiếp.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Hai tia phân giác của hai góc kề bù vuông góc với nhau.

+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng $180^{\circ}$ thì tứ giác đó nội tiếp được đường tròn.

Lời giải:

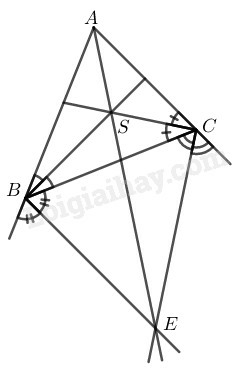
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 2)

Ta có: $B S ⊥ B E$ (tính chất: Hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

$\Rightarrow \hat{S B E} = 90^{\circ}$

Tương tự: $C S ⊥ C E$ (tính chất: Hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

$\Rightarrow \hat{S C E} = 90^{\circ}$

Xét tứ giác $B S C E$ ta có: $\hat{S B E} + \hat{S C E} = 180^{\circ}$ mà hai góc này ở vị trí đối nhau nên tứ giác $B S C E$ nội tiếp.

Bài 41 trang 106 SBT Toán 9 tập 2: Cho tam giác cân

A B C

có đáy

B C

và

\hat{A} = 20^{0}

. Trên nửa mặt phẳng bờ

A B

không chứa điểm

C

lấy điểm

D

sao cho

D A = D B

và

\hat{D A B} = 40^{0}

. Gọi

E

là giao điểm của

A B

và

C D .

$a)$ Chứng minh $A C B D$ là tứ giác nội tiếp

$b)$ Tính $\hat{A E D}$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong tam giác cân, hai góc ở đáy bằng nhau.

+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng $180^{\circ}$ thì tứ giác đó nội tiếp được đường tròn.

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Lời giải:

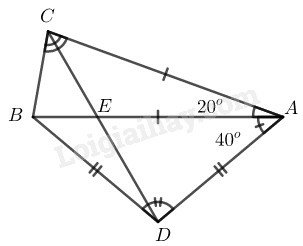
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 3)

$a)$ $∆ A B C$ cân tại $A (g t) .$

$\Rightarrow \hat{A C B} = \hat{A B C}$ (tính chất tam giác cân)

$\Rightarrow \hat{A C B} = \frac{180^{\circ} - \hat{A}}{2}$ $= \frac{180^{\circ} - 20^{\circ}}{2} = 80^{\circ}$

$∆ D A B$ cân tại $D$ (do $D A = D B)$

$\Rightarrow \hat{D B A} = \hat{D A B}$ (tính chất tam giác cân) mà $\hat{D A B} = 40^{\circ}$ (gt) $\Rightarrow \hat{D B A} = 40^{\circ}$

$\hat{A D B} = 180^{\circ} - (\hat{D A B} + \hat{D B A})$ $= 180^{\circ} - (40^{\circ} + 40^{\circ}) = 100^{\circ}$

Trong tứ giác $A C B D$ ta có: $\hat{A C B} + \hat{A D B}$ $= 80^{\circ} + 100^{\circ} = 180^{\circ}$

Vậy: Tứ giác $A C B D$ nội tiếp.

$b)$ Vì tứ giác $A C B D$ nội tiếp (câu a) nên xét đường tròn ngoại tiếp tứ giác $A C B D$ ta có:

+) $\hat{B A C} = \frac{1}{2} s đ \overset{⏜}{B C}$ (tính chất góc nội tiếp)

$\Rightarrow$ sđ $\overset{⏜}{B C}$ $= 2 \hat{B A C} = {2.20}^{\circ} = 40^{\circ}$

+) $\hat{D B A} = \frac{1}{2} s đ \overset{⏜}{A D}$ (tính chất góc nội tiếp)

$\Rightarrow$ sđ $\overset{⏜}{A D}$ $= 2 \hat{D B A} = {2.40}^{\circ} = 80^{\circ}$

+) $\hat{A E D}$ là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác $A C B D$

$\hat{A E D} = \frac{1}{2} (s đ \overset{⏜}{B C} + s đ \overset{⏜}{A D})$ $= \frac{40^{\circ} + 80^{\circ}}{2} = 60^{\circ}$

Bài 42 trang 107 SBT Toán 9 tập 2: Cho ba đường tròn cùng đi qua một điểm

P .

Gọi các giao điểm khác

P

của hai trong ba đường tròn đó là

A, B, C .

Từ một điểm

D

(khác điểm

P

) trên đường tròn

(P B C)

kẻ các tia

D B, D C

cắt các đường tròn

(P A B)

và

(P A C)

lần lượt tại

M, N .

Chứng minh ba điểm

M, A, N

thẳng hàng.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng $180^{\circ} .$

+) Chứng minh ba điểm thẳng hàng: Nếu $\hat{A B D} + \hat{D B C} = 180^{\circ}$ thì $A, B, C$ thẳng hàng.

Lời giải:

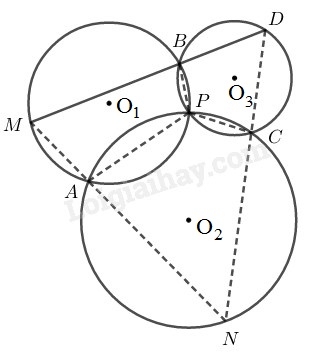
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 4)

Gọi ba đường tròn tâm $O_{1}, O_{2}, O_{3} .$

$(O_{1})$ cắt $(O_{2})$ tại $A;$ $(O_{1})$ cắt $(O_{3})$ tại $B .$

$(O_{2})$ cắt $(O_{3})$ tại $C .$ Suy ra $D$ là điểm nằm trên đường tròn $(O_{3}) .$

$B D$ cắt $(O_{1})$ tại $M,$ $D C$ cắt $(O_{2})$ tại $N .$

Nối $P A, P B, P C,$ $M A, N A .$

Ta có tứ giác $A P B M$ nội tiếp trong đường tròn $(O_{1}) .$

Nên $\hat{M A P} + \hat{M B P} = 180^{\circ}$ (tính chất tứ giác nội tiếp)

Mà $\hat{M B P} + \hat{P B D} = 180^{\circ}$ (hai góc kề bù)

Suy ra: $\hat{M A P} = \hat{P B D}$ $(1)$

Ta có: Tứ giác $A P C N$ nội tiếp trong đường tròn $(O_{2})$

Nên $\hat{N A P} + \hat{N C P} = 180^{\circ}$ (tính chất tứ giác nội tiếp)

Mà $\hat{N C P} + \hat{P C D} = 180^{\circ}$ (hai góc kề bù)

Suy ra: $\hat{N A P} = \hat{P C D}$ $(2)$

Tứ giác $B P C D$ nội tiếp trong đường tròn $(O_{3})$

$\Rightarrow \hat{P B D} + \hat{P C D} = 180^{\circ}$ (tính chất tứ giác nội tiếp) $(3)$

Từ $(1),$ $(2)$ và $(3)$ suy ra: $\hat{M A P} + \hat{N A P} = 180^{\circ}$

Vậy ba điểm $M, A, N$ thẳng hàng.

Bài 43 trang 107 SBT Toán 9 tập 2: Cho hai đoạn thẳng

A C

và

B D

cắt nhau tại

E .

Biết

A E . E C = B E . E D

. Chứng minh bốn điểm

A, B, C, D

cùng nằm trên một đường tròn.

Phương pháp giải:

Ta sử dụng kiến thức:

+) Các điểm cùng nhìn một cạnh cố định dưới góc bằng nhau thì các điểm đó cùng thuộc một cung chứa góc vẽ trên cạnh cố định.

+) Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.

Lời giải:

SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 5)

Từ $A E . E C = B E . E D (g t)$

$\Rightarrow \frac{A E}{E D} = \frac{B E}{E C}$

Xét $∆ A E B$ và $∆ D E C :$

$\frac{A E}{E D} = \frac{B E}{E C}$

$\hat{A E B} = \hat{D E C}$ (đối đỉnh)

Suy ra: $∆ A E B$ đồng dạng $∆ D E C (c . g . c)$

$\Rightarrow \hat{B A E} = \hat{C D E}$ hay $\hat{B A C} = \hat{C D B}$

Từ đó: $A$ và $D$ nhìn đoạn $B C$ cố định dưới một góc bằng nhau nên $4$ điểm $A, B, C, D$ nằm trên một đường tròn.

Bài tập bổ sung (trang 6 SBT Toán 9)

Bài 7.1 trang 107 SBT Toán 9 tập 2: Cho tam giác

A B C

có ba góc nhọn. Vẽ các đường cao

A I, B K, C L

của tam giác ấy.Gọi

H

là giao điểm của các đường cao vừa vẽ.

$a)$ Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm $A, B, C, H, I, K, L$

$b)$ Chứng minh $\hat{L B H}, \hat{L I H}, \hat{K I H}$ và $\hat{K C H}$ là $4$ góc bằng nhau.

$c)$ Chứng minh $K B$ là tia phân giác của $\hat{L K I} .$

Phương pháp giải:

Ta sử dụng kiến thức:

+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng $180^{\circ}$ thì tứ giác đó nội tiếp được đường tròn.

+) Tứ giác có hai đỉnh cùng nhìn một cạnh dưới một góc vuông là tứ giác nội tiếp.

+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

Lời giải:

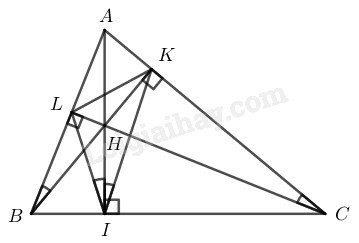
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 6)

Vì $∆ A B C$ là tam giác nhọn nên ba đường cao cắt nhau tại điểm $H$ nằm trong tam giác $A B C .$

$a)$ Tứ giác $A K H L$ có: $\hat{A K H} + \hat{A L H} = 90^{\circ} + 90^{\circ} = 180^{\circ}$

Nên tứ giác $A K H L$ nội tiếp.

$+)$ Tứ giác $B I H L$ có: $\hat{B I H} + \hat{B L H} = 90^{\circ} + 90^{\circ} = 180^{\circ}$

Nên tứ giác $B I H L$ nội tiếp.

$+)$ Tứ giác $C I H K$ có: $\hat{C I H} + \hat{C K H} = 90^{\circ} + 90^{\circ} = 180^{\circ}$

Nên tứ giác $C I H K$ nội tiếp.

$+)$ Tứ giác $A B I K$ có: $\hat{A K B} = 90^{\circ}; \hat{A I B} = 90^{\circ}$

$K$ và $I$ nhìn đoạn $A B$ dưới một góc vuông nên tứ giác $A B I K$ nội tiếp.

$+)$ Tứ giác $B C K L$ có $\hat{B K C} = 90^{\circ}; \hat{B L C} = 90^{\circ}$

Suy ra $K$ và $L$ nhìn đoạn $B C$ dưới một góc vuông nên tứ giác $B C K L$ nội tiếp.

$+)$ Tứ giác $A C I L$ có $\hat{A I C} = 90^{\circ}; \hat{A L C} = 90^{\circ}$

Suy ra $I$ và $L$ nhìn đoạn $A C$ dưới một góc vuông nên tứ giác $A C I L$ nội tiếp.

$b)$ Tứ giác $B I H L$ nội tiếp.

$\Rightarrow \hat{L B H} = \hat{L I H}$ $($ $2$ góc nội tiếp cùng chắn cung nhỏ $\overset{⏜}{L H}$ $)$ $(1)$

Tứ giác $C I H K$ nội tiếp.

$\Rightarrow \hat{H I K} = \hat{H C K}$ $(2$ góc nội tiếp cùng chắn cung nhỏ $\overset{⏜}{H K}$ $)$ $(2)$

Tứ giác $B C K L$ nội tiếp.

$\Rightarrow \hat{L B K} = \hat{L C K}$ $(2$ góc nội tiếp cùng chắn cung nhỏ $\overset{⏜}{L K}$ ) hay $\hat{L B H} = \hat{H C K}$ $(3)$

Từ $(1),$ $(2)$ và $(3)$ suy ra $\hat{L B H} = \hat{L I H} = \hat{K I H}$ $= \hat{K C H}$

c) Tứ giác $C I H K$ nội tiếp.

$\Rightarrow \hat{I C H} = \hat{I K H}$ $($ $2$ góc nội tiếp cùng chắn cung nhỏ $\overset{⏜}{I H}$ $)$ $(*)$

Tứ giác $L K C B$ nội tiếp.

$\Rightarrow \hat{L C B} = \hat{L K B}$ $($ $2$ góc nội tiếp cùng chắn cung nhỏ $\overset{⏜}{L B}$ $)$ $(* *)$

Từ (*) và (**) suy ra $\hat{L K H} = \hat{H K I}$ . Vậy $K B$ là tia phân giác của $\hat{L K I} .$

Bài 7.2 trang 107 SBT Toán 9 tập 2: Cho đường tròn tâm

O

bán kính

R

và hai dây

A B,

C D

bất kì. Gọi

M

là điểm chính giữa của cung nhỏ

A B .

Gọi

E

và

F

tương ứng là giao điểm của

M C,

M D

với dây

A B .

Gọi

I

và

J

tương ứng là giao điểm của

D E,

C F

với đường tròn

(O) .

Chứng minh

I J

song song với

A B .

Phương pháp giải:

Ta sử dụng kiến thức:

+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng $180^{\circ}$ thì tứ giác đó nội tiếp được đường tròn.

+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.

+) Nếu $C$ là một điểm trên cung $A B$ thì: $s đ \overset{⏜}{A B} = s đ \overset{⏜}{A C} + s đ \overset{⏜}{C B} .$

+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

Lời giải:

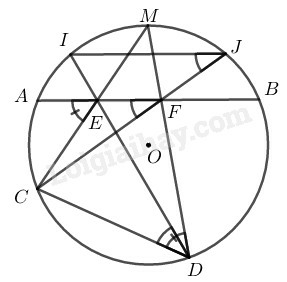
SBT Toán 9 Bài 7: Tứ giác nội tiếp | Giải SBT Toán lớp 9 (ảnh 7)

Xét đường tròn $(O)$ có $M$ là điểm chính giữa của cung nhỏ $\overset{⏜}{A B}$ .

Suy ra $\overset{⏜}{M A}$ = $\overset{⏜}{M B}$

Lại có: $\hat{A E C} = \frac{1}{2} (s đ \overset{⏜}{A C} + s đ \overset{⏜}{M B}$ ) (góc có đỉnh ở trong đường tròn)

$\hat{C D M} = \frac{1}{2} s đ \overset{⏜}{M A C}$ (tính chất góc nội tiếp) hay $\hat{C D F} = \frac{1}{2} (s đ \overset{⏜}{M A} + s đ \overset{⏜}{A C})$ $= \frac{1}{2} (s đ \overset{⏜}{A C} + s đ \overset{⏜}{M B})$