Với giải vở thực hành Toán 7 Bài 6: Số vô tỉ. Căn bậc hai số học sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VTH Toán 7. Mời các bạn đón xem:

Giải VTH Toán lớp 7 Bài 6: Số vô tỉ. Căn bậc hai số học

Câu 1 trang 27 VTH Toán 7 Tập 1: Độ dài cạnh hình vuông có diện tích bằng 20,25 m² là

A. 3,75 m;

B. 4,5 m;

C. 5,25 m;

D. 5,05 m.

Lời giải:

Đáp án đúng là B

Độ dài cạnh hình vuông là: $\sqrt{20,25}=4,5$ m.

Câu 2 trang 27 VTH Toán 7 Tập 1: Nếu a < 0 thì

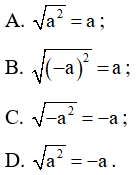
Lời giải:

Đáp án đúng là D

Vì a < 0 nên $\sqrt{a^2}=\left|a\right|=-a$.

Câu 3 trang 27 VTH Toán 7 Tập 1: Sử dụng máy tính cầm tay tính căn bậc hai số học của 19 và làm tròn kết quả với độ chính xác 0,0005 ta được:

A. 4,3;

B. 4,35;

C. 4,36;

D. 4,359.

Lời giải:

Đáp án đúng là D

Ta có: $\sqrt{19}=4,\mathrm{358898944...}$

Độ chính xác 0,0005 thì cần làm tròn đến hàng phần nghìn, chữ số hàng làm tròn là 8, chữ số là 8 (8 > 5) nên ta có: $\sqrt{19}=4,\mathrm{358898944...}$ ≈ 4,359.

Bài 1 (2.6) trang 27 VTH Toán 7 Tập 1: Cho biết 153² = 23409. Hãy tính $\sqrt{23409}.$

Lời giải:

Theo định nghĩa, $\sqrt{23409}.$ là căn bậc hai số học thỏa mãn 23 409 là số không âm.

Mà 153² = 23409 (giả thiết) và 153 là số không âm, suy ra$\sqrt{23409}=153.$

Bài 2 (2.7) trang 27 VTH Toán 7 Tập 1: Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:

a) 9;                          

b) 16;                        

c) 81;                        

d) 121.

Lời giải:

12 số tự nhiên đầu tiên là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11. Bình phương các số này ta được 0² = 0; 1² = 1; 2² = 4; 3² = 9; 4² = 16; 5² = 25; 6² = 36; 7² = 49; 8² = 64; 9² = 81; 10² = 100; 11² = 121. Từ đó tương tự bài tập 1) ta có

Bài 3 (2.8) trang 27 VTH Toán 7 Tập 1: Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:

Vì 324 = 2² . 3⁴ = ${\left({2.3}^2\right)}^2$ = 18² nên $\sqrt{324}=18.$ Tính căn bậc hai số học của 129600.

Lời giải:

Phân tích 129600 ra thừa số nguyên tố ta được 129 600 = 2⁶ . 3⁴ . 5² = ${\left(2^3{.3}^2.5\right)}^2$ = 360². Do đó căn bậc hai số học của 129 600 là 360 (lập luận như $\sqrt{324}$).

Bài 4 (2.9) trang 28 VTH Toán 7 Tập 1: Tính độ dài cạnh của hình vuông có diện tích bằng:

a) 81 dm²;                 

b) 3600 m²;               

c) 1 ha.

Lời giải:

Ta đã biết: Nếu a là diện tích của một hình vuông thì độ dài cạnh của hình vuông bằng $\sqrt{a}$. Do đó:

a) Nếu diện tích hình vuông bằng 81 dm² thì độ dài cạnh hình vuông là $\sqrt{81}$. Mà 81 = 9² và 9 > 0 nên $\sqrt{81}=9$. Độ dài cạnh của hình vuông là 9 dm.

b) Nếu diện tích hình vuông bằng 3 600 m² thì độ dài cạnh hình vuông là $\sqrt{3600}$. Mà 3600 = 60² và 60 > 0 nên $\sqrt{3600}=60$. Độ dài cạnh của hình vuông là 60 m.

c) Vì 1 ha = 10 000 m² nên nếu diện tích hình vuông bằng 1ha thì độ dài cạnh hình vuông là $\sqrt{10000}$. Mà 10 000 = 100² và 100 > 0 nên $\sqrt{10000}=100$. Độ dài cạnh hình vuông là 100 m.

Bài 5 (2.10) trang 28 VTH Toán 7 Tập 1: Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn kết quả với độ chính xác 0,005.

a) 3;                          

b) 41;                        

c) 2021.

Lời giải:

Muốn làm tròn kết quả với độ chính xác 0,005 ta cần làm tròn đến hàng phần trăm. Sử dụng máy tính cầm tay ta được:

Bài 6 (2.11) trang 28 VTH Toán 7 Tập 1: Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét? (làm tròn kết quả đến hàng phần mười).

Lời giải:

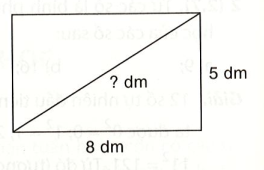
Vì bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó (theo gợi ý của đề bài) và hình chữ nhật đã cho có chiều dài 8 dm; chiều rộng là 5 dm (giả thiết) nên độ dài đường chéo của hình chữ nhật là: $\sqrt{8^2+5^2}=\sqrt{89}$. Sử dụng máy tính cầm tay ta tính được $\sqrt{89}\approx 9,\mathrm{43398...}$. Làm tròn kết quả đến hàng phần mười ta được 9,4. Độ dài đường chéo hình chữ nhật là 9,4 dm.

Bài 7 (2.12) trang 28 VTH Toán 7 Tập 1: Để lát một mảnh sân hình vuông có diện tích 100 m², người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm? (coi các mạch ghép là không đáng kể).

Lời giải:

Ta đã biết: Nếu a là diện tích của một hình vuông thì độ dài cạnh hình vuông là $\sqrt{a}$. Do đó, nếu mảnh sân hình vuông có diện tích 100 m². Mà 100 = 10² nên $\sqrt{100}=10$. Do đó, độ dài cạnh sân hình vuông là 10 m = 1 000 cm. Vì mỗi viên gạch hình vuông có cạnh dài 50cm nên nếu xếp các viên gạch dọc theo cạnh sân ta được: 1 000 : 50 = 20 viên gạch. Để lát hết diện tích mặt sân thì số viên gạch cần dùng là: 20.20 = 400 viên gạch.