Với giải Bài 37 trang 94 Toán lớp 9 chi tiết trong Ôn tập chương I Hình học giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9: Ôn tập chương I Hình học

Bài 37 trang 94 Toán lớp 9 tập 1: Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào ?

Lời giải:

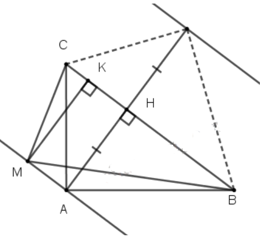
a)

Xét tam giác ABC

Có:

$$\begin{gathered} {\mathrm{AB}}^2+{\mathrm{AC}}^2=6^2+4,5^2=56,25 \\ {\mathrm{BC}}^2=7,5^2=56,25 \\ \Rightarrow {\mathrm{BC}}^2={\mathrm{AB}}^2+{\mathrm{AC}}^2 \end{gathered}$$

Do đó tam giác ABC vuông tại A (định lí Py-ta-go đảo)

Xét tam giác ABC vuông tại A

Áp dụng tỉ số lượng giác của góc nhọn ta có:

$$\begin{gathered} \mathrm{sinB}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{4,5}{7,5}=\frac{3}{5}\Rightarrow \widehat{\mathrm{B}}={36}^{\mathrm{o}}52\text{'} \\ \mathrm{sinC}=\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{6}{7,5}=\frac{4}{5}\Rightarrow \widehat{\mathrm{C}}={53}^{\mathrm{o}}8\text{'} \end{gathered}$$

Áp dụng hệ thức về góc và cạnh trong tam giác vuông ta có:

$$\begin{gathered} \frac{1}{{\mathrm{AH}}^2}=\frac{1}{{\mathrm{AB}}^2}+\frac{1}{{\mathrm{AC}}^2}=\frac{1}{6^2}+\frac{1}{4,5^2}=\frac{25}{324} \\ \Rightarrow {\mathrm{AH}}^2=\frac{324}{25}\Rightarrow \mathrm{AH}=\sqrt{\frac{324}{25}}=3,6 \left(\mathrm{cm}\right) \end{gathered}$$

b)

Lấy điểm M bất kì, kẻ $\mathrm{MK}\perp \mathrm{BC}$ tại K

Diện tích của tam giác MBC là: ${\mathrm{S}}_{\mathrm{\Delta MBC}}=\frac{1}{2}\mathrm{MK}.\mathrm{BC}$

Diện tích của tam giác ABC là: ${\mathrm{S}}_{\mathrm{\Delta ABC}}=\frac{1}{2}\mathrm{AH}.\mathrm{BC}$

Để diện tích tam giác MBC bằng diện tích tam giác ABC thì

$$\begin{gathered} \frac{1}{2}\mathrm{MK}.\mathrm{BC}=\frac{1}{2}\mathrm{AH}.\mathrm{BC} \\ \iff \mathrm{MK}=\mathrm{AH}=3,6 \left(\mathrm{cm}\right) \end{gathered}$$

hay M cách BC một khoảng không đổi bằng AH.

Vậy tập hợp các điểm M là hai đường thẳng song song với BC và cách BC một khoảng bằng 3,6cm.